Part IA, 2009, Paper 2

Differential Equations

• Paper 2, Section I, C

  Differential Equations | Part IA, 2009

  Solve the differential equation

  $$\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}-5 \frac{\mathrm{d} y}{\mathrm{~d} x}+6 y=\mathrm{e}^{3 x}$$

  subject to the conditions $y=\mathrm{d} y / \mathrm{d} x=0$ when $x=0$.

  comment

• Paper 2, Section I, C

  Differential Equations | Part IA, 2009

  The size of the population of ducks living on the pond of a certain Cambridge college is governed by the equation

  $$\frac{\mathrm{d} N}{\mathrm{~d} t}=\alpha N-N^{2}$$

  where $N=N(t)$ is the number of ducks at time $t$ and $\alpha$ is a positive constant. Given that $N(0)=2 \alpha$, find $N(t)$. What happens as $t \rightarrow \infty$ ?

  comment

• Paper 2, Section II, $7 \mathrm{C}$

  Differential Equations | Part IA, 2009

  Consider the differential equation

  $$x \frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}+(c-x) \frac{\mathrm{d} y}{\mathrm{~d} x}-y=0,$$

  where $c$ is a constant with $0<c<1$. Determine two linearly independent series solutions about $x=0$, giving an explicit expression for the coefficient of the general term in each series.

  Determine the solution of

  $$x \frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}+(c-x) \frac{\mathrm{d} y}{\mathrm{~d} x}-y=x$$

  for which $y(0)=0$ and $\mathrm{d} y / \mathrm{d} x$ is finite at $x=0$.

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  Consider the second-order ordinary differential equation

  $$\ddot{x}+2 k \dot{x}+\omega^{2} x=0,$$

  where $x=x(t)$ and $k$ and $\omega$ are constants with $k>0$. Calculate the general solution in the cases (i) $k<\omega$, (ii) $k=\omega$, (iii) $k>\omega$.

  Now consider the system

  $$\ddot{x}+2 k \dot{x}+\omega^{2} x= \begin{cases}a & \text { when } \dot{x}>0 \\ 0 & \text { when } \dot{x} \leqslant 0\end{cases}$$

  with $x(0)=x_{1}, \dot{x}(0)=0$, where $a$ and $x_{1}$ are positive constants. In the case $k<\omega$ find $x(t)$ in the ranges $0 \leqslant t \leqslant \pi / p$ and $\pi / p \leqslant t \leqslant 2 \pi / p$, where $p=\sqrt{\omega^{2}-k^{2}}$. Hence, determine the value of $x_{1}$ for which $x(t)$ is periodic. For $k>\omega$ can $x(t)$ ever be periodic? Justify your answer.

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  Consider the first-order ordinary differential equation

  $$\frac{\mathrm{d} y}{\mathrm{~d} x}=f_{1}(x) y+f_{2}(x) y^{p}$$

  where $y \geqslant 0$ and $p$ is a positive constant with $p \neq 1$. Let $u=y^{1-p}$. Show that $u$ satisfies

  $$\frac{\mathrm{d} u}{\mathrm{~d} x}=(1-p)\left[f_{1}(x) u+f_{2}(x)\right]$$

  Hence, find the general solution of equation $(*)$ when $f_{1}(x)=1, f_{2}(x)=x$.

  Now consider the case $f_{1}(x)=1, f_{2}(x)=-\alpha^{2}$, where $\alpha$ is a non-zero constant. For $p>1$ find the two equilibrium points of equation $(*)$, and determine their stability. What happens when $0<p<1$ ?

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  (a) The function $y(x, t)$ satisfies the forced wave equation

  $$\frac{\partial^{2} y}{\partial x^{2}}-\frac{\partial^{2} y}{\partial t^{2}}=4$$

  with initial conditions $y(x, 0)=\sin x$ and $\partial y / \partial t(x, 0)=0$. By making the change of variables $u=x+t$ and $v=x-t$, show that

  $$\frac{\partial^{2} y}{\partial u \partial v}=1$$

  Hence, find $y(x, t)$.

  (b) The thickness of an axisymmetric drop of liquid spreading on a flat surface satisfies

  $$\frac{\partial h}{\partial t}=\frac{1}{r} \frac{\partial}{\partial r}\left(r h^{3} \frac{\partial h}{\partial r}\right),$$

  where $h=h(r, t)$ is the thickness of the drop, $r$ is the radial coordinate on the surface and $t$ is time. The drop has radius $R(t)$. The boundary conditions are that $\partial h / \partial r=0$ at $r=0$ and $h(r, t) \propto(R(t)-r)^{1 / 3}$ as $r \rightarrow R(t)$.

  Show that

  $$M=\int_{0}^{R(t)} r h \mathrm{~d} r$$

  is independent of time. Given that $h(r, t)=f\left(r / t^{\alpha}\right) t^{-1 / 4}$ for some function $f$ (which need not be determined) and that $R(t)$ is proportional to $t^{\alpha}$, find $\alpha$.

  comment

Probability

• Paper 2, Section $I$, F

  Probability | Part IA, 2009

  Prove the law of total probability: if $A_{1}, \ldots, A_{n}$ are pairwise disjoint events with $\mathbb{P}\left(A_{i}\right)>0$, and $B \subseteq A_{1} \cup \ldots \cup A_{n}$ then $\mathbb{P}(B)=\sum_{i=1}^{n} \mathbb{P}\left(A_{i}\right) \mathbb{P}\left(B \mid A_{i}\right)$.

  There are $n$ people in a lecture room. Their birthdays are independent random variables, and each person's birthday is equally likely to be any of the 365 days of the year. By using the bound $1-x \leqslant e^{-x}$ for $0 \leqslant x \leqslant 1$, prove that if $n \geqslant 29$ then the probability that at least two people have the same birthday is at least $2 / 3$.

  [In calculations, you may take $\sqrt{1+8 \times 365 \ln 3}=56.6$.]

  comment

• Paper 2, Section I, F

  Probability | Part IA, 2009

  Consider a pair of jointly normal random variables $X_{1}, X_{2}$, with mean values $\mu_{1}$, $\mu_{2}$, variances $\sigma_{1}^{2}, \sigma_{2}^{2}$ and correlation coefficient $\rho$ with $|\rho|<1$.

  (a) Write down the joint probability density function for $\left(X_{1}, X_{2}\right)$.

  (b) Prove that $X_{1}, X_{2}$ are independent if and only if $\rho=0$.

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  Let $A_{1}, A_{2}$ and $A_{3}$ be three pairwise disjoint events such that the union $A_{1} \cup A_{2} \cup A_{3}$ is the full event and $\mathbb{P}\left(A_{1}\right), \mathbb{P}\left(A_{2}\right), \mathbb{P}\left(A_{3}\right)>0$. Let $E$ be any event with $\mathbb{P}(E)>0$. Prove the formula

  $$\mathbb{P}\left(A_{i} \mid E\right)=\frac{\mathbb{P}\left(A_{i}\right) \mathbb{P}\left(E \mid A_{i}\right)}{\sum_{j=1,2,3} \mathbb{P}\left(A_{j}\right) \mathbb{P}\left(E \mid A_{j}\right)}$$

  A Royal Navy speedboat has intercepted an abandoned cargo of packets of the deadly narcotic spitamin. This sophisticated chemical can be manufactured in only three places in the world: a plant in Authoristan (A), a factory in Bolimbia (B) and the ultramodern laboratory on board of a pirate submarine Crash (C) cruising ocean waters. The investigators wish to determine where this particular cargo comes from, but in the absence of prior knowledge they have to assume that each of the possibilities A, B and C is equally likely.

  It is known that a packet from A contains pure spitamin in $95 \%$ of cases and is contaminated in $5 \%$ of cases. For B the corresponding figures are $97 \%$ and $3 \%$, and for $\mathrm{C}$ they are $99 \%$ and $1 \%$.

  Analysis of the captured cargo showed that out of 10000 packets checked, 9800 contained the pure drug and the remaining 200 were contaminated. On the basis of this analysis, the Royal Navy captain estimated that $98 \%$ of the packets contain pure spitamin and reported his opinion that with probability roughly $0.5$ the cargo was produced in B and with probability roughly $0.5$ it was produced in C.

  Assume that the number of contaminated packets follows the binomial distribution $\operatorname{Bin}(10000, \delta / 100)$ where $\delta$ equals 5 for $A, 3$ for $B$ and 1 for C. Prove that the captain's opinion is wrong: there is an overwhelming chance that the cargo comes from B.

  [Hint: Let $E$ be the event that 200 out of 10000 packets are contaminated. Compare the ratios of the conditional probabilities $\mathbb{P}(E \mid A), \mathbb{P}(E \mid B)$ and $\mathbb{P}(E \mid C)$. You may find it helpful that $\ln 3 \approx 1.09861$ and $\ln 5 \approx 1.60944$. You may also take $\ln (1-\delta / 100) \approx-\delta / 100$.]

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  Let $X$ and $Y$ be two independent uniformly distributed random variables on $[0,1]$. Prove that $\mathbb{E} X^{k}=\frac{1}{k+1}$ and $\mathbb{E}(X Y)^{k}=\frac{1}{(k+1)^{2}}$, and find $\mathbb{E}(1-X Y)^{k}$, where $k$ is a non-negative integer.

  Let $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)$ be $n$ independent random points of the unit square $\mathcal{S}=\{(x, y): 0 \leqslant x, y \leqslant 1\}$. We say that $\left(X_{i}, Y_{i}\right)$ is a maximal external point if, for each $j=1, \ldots, n$, either $X_{j} \leqslant X_{i}$ or $Y_{j} \leqslant Y_{i}$. (For example, in the figure below there are three maximal external points.) Determine the expected number of maximal external points.

  

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  No-one in their right mind would wish to be a guest at the Virtual Reality Hotel. See the diagram below showing a part of the floor plan of the hotel where rooms are represented by black or white circles. The hotel is built in a shape of a tree: there is one room (reception) situated at level 0, three rooms at level 1 , nine at level 2 , and so on. The rooms are joined by corridors to their neighbours: each room has four neighbours, apart from the reception, which has three neighbours. Each corridor is blocked with probability $1 / 3$ and open for passage in both directions with probability $2 / 3$, independently for different corridors. Every room at level $N$, where $N$ is a given very large number, has an open window through which a guest can (and should) escape into the street. An arriving guest is placed in the reception and then wanders freely, insofar as the blocked corridors allow.

  

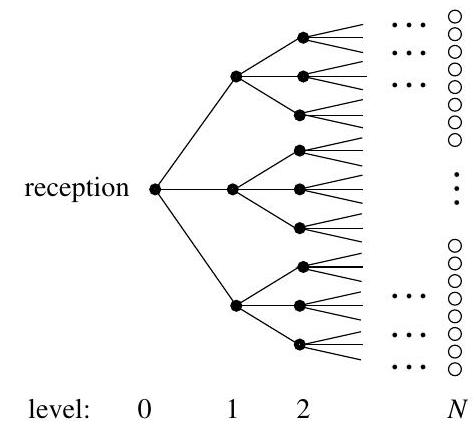
  (a) Prove that the probability that the guest will not escape is close to a solution of the equation $\phi(t)=t$, where $\phi(t)$ is a probability-generating function that you should specify.

  (b) Hence show that the guest's chance of escape is approximately $(9-3 \sqrt{3}) / 4$.

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  I throw two dice and record the scores $S_{1}$ and $S_{2}$. Let $X$ be the sum $S_{1}+S_{2}$ and $Y$ the difference $S_{1}-S_{2}$.

  (a) Suppose that the dice are fair, so the values $1, \ldots, 6$ are equally likely. Calculate the mean and variance of both $X$ and $Y$. Find all the values of $x$ and $y$ at which the probabilities $\mathbb{P}(X=x), \mathbb{P}(Y=y)$ are each either greatest or least. Determine whether the random variables $X$ and $Y$ are independent.

  (b) Now suppose that the dice are unfair, and that they give the values $1, \ldots, 6$ with probabilities $p_{1}, \ldots, p_{6}$ and $q_{1}, \ldots, q_{6}$, respectively. Write down the values of $\mathbb{P}(X=$ 2), $\mathbb{P}(X=7)$ and $\mathbb{P}(X=12)$. By comparing $\mathbb{P}(X=7)$ with $\sqrt{\mathbb{P}(X=2) \mathbb{P}(X=12)}$ and applying the arithmetic-mean-geometric-mean inequality, or otherwise, show that the probabilities $\mathbb{P}(X=2), \mathbb{P}(X=3), \ldots, \mathbb{P}(X=12)$ cannot all be equal.

  comment