Part IA, 2008

Analysis I

• 1.I $. 3 \mathrm{~F} \quad$

  Analysis I | Part IA, 2008

  State the ratio test for the convergence of a series.

  Find all real numbers $x$ such that the series

  $$\sum_{n=1}^{\infty} \frac{x^{n}-1}{n}$$

  converges.

  comment

• 1.I.4E

  Analysis I | Part IA, 2008

  Let $f:[0,1] \rightarrow \mathbb{R}$ be Riemann integrable, and for $0 \leqslant x \leqslant 1$ set $F(x)=\int_{0}^{x} f(t) d t$.

  Assuming that $f$ is continuous, prove that for every $0<x<1$ the function $F$ is differentiable at $x$, with $F^{\prime}(x)=f(x)$.

  If we do not assume that $f$ is continuous, must it still be true that $F$ is differentiable at every $0<x<1$ ? Justify your answer.

  comment

• 1.II $. 9 \mathrm{~F} \quad$

  Analysis I | Part IA, 2008

  Investigate the convergence of the series (i) $\sum_{n=2}^{\infty} \frac{1}{n^{p}(\log n)^{q}}$ (ii) $\sum_{n=3}^{\infty} \frac{1}{n(\log \log n)^{r}}$

  for positive real values of $p, q$ and $r$.

  [You may assume that for any positive real value of $\alpha, \log n<n^{\alpha}$ for $n$ sufficiently large. You may assume standard tests for convergence, provided that they are clearly stated.]

  comment

• 1.II.10D

  Analysis I | Part IA, 2008

  (a) State and prove the intermediate value theorem.

  (b) An interval is a subset $I$ of $\mathbb{R}$ with the property that if $x$ and $y$ belong to $I$ and $x<z<y$ then $z$ also belongs to $I$. Prove that if $I$ is an interval and $f$ is a continuous function from $I$ to $\mathbb{R}$ then $f(I)$ is an interval.

  (c) For each of the following three pairs $(I, J)$ of intervals, either exhibit a continuous function $f$ from $I$ to $\mathbb{R}$ such that $f(I)=J$ or explain briefly why no such continuous function exists: (i) $I=[0,1], \quad J=[0, \infty)$; (ii) $I=(0,1], \quad J=[0, \infty)$; (iii) $I=(0,1], \quad J=(-\infty, \infty)$.

  comment

• 1.II.11D

  Analysis I | Part IA, 2008

  (a) Let $f$ and $g$ be functions from $\mathbb{R}$ to $\mathbb{R}$ and suppose that both $f$ and $g$ are differentiable at the real number $x$. Prove that the product $f g$ is also differentiable at $x$.

  (b) Let $f$ be a continuous function from $\mathbb{R}$ to $\mathbb{R}$ and let $g(x)=x^{2} f(x)$ for every $x$. Prove that $g$ is differentiable at $x$ if and only if either $x=0$ or $f$ is differentiable at $x$.

  (c) Now let $f$ be any continuous function from $\mathbb{R}$ to $\mathbb{R}$ and let $g(x)=f(x)^{2}$ for every $x$. Prove that $g$ is differentiable at $x$ if and only if at least one of the following two possibilities occurs:

  (i) $f$ is differentiable at $x$;

  (ii) $f(x)=0$ and

  $$\frac{f(x+h)}{|h|^{1 / 2}} \longrightarrow 0 \quad \text { as } \quad h \rightarrow 0$$

  comment

• 1.II.12E

  Analysis I | Part IA, 2008

  Let $\sum_{n=0}^{\infty} a_{n} z^{n}$ be a complex power series. Prove that there exists an $R \in[0, \infty]$ such that the series converges for every $z$ with $|z|<R$ and diverges for every $z$ with $|z|>R$.

  Find the value of $R$ for each of the following power series: (i) $\sum_{n=1}^{\infty} \frac{1}{n^{2}} z^{n}$; (ii) $\sum_{n=0}^{\infty} z^{n !}$.

  In each case, determine at which points on the circle $|z|=R$ the series converges.

  comment

Differential Equations

• 2.I.1A

  Differential Equations | Part IA, 2008

  Let $a$ be a positive constant. Find the solution to the differential equation

  $$\frac{d^{4} y}{d x^{4}}-a^{4} y=\mathrm{e}^{-a x}$$

  that satisfies $y(0)=1$ and $y \rightarrow 0$ as $x \rightarrow \infty$.

  comment

• 2.I.2A

  Differential Equations | Part IA, 2008

  Find the fixed points of the difference equation

  $$u_{n+1}=\lambda u_{n}\left(1-u_{n}^{2}\right)$$

  Show that a stable fixed point exists when $-1<\lambda<1$ and also when $1<\lambda<2$.

  comment

• 2.II.5A

  Differential Equations | Part IA, 2008

  Two cups of hot tea at temperatures $T_{1}(t)$ and $T_{2}(t)$ cool in a room at ambient constant temperature $T_{\infty}$. Initially $T_{1}(0)=T_{2}(0)=T_{0}>T_{\infty}$.

  Cup 1 has cool milk added instantaneously at $t=1$; in contrast, cup 2 has cool milk added at a constant rate for $1 \leqslant t \leqslant 2$. Briefly explain the use of the differential equations

  $$\begin{aligned} &\frac{d T_{1}}{d t}=-a\left(T_{1}-T_{\infty}\right)-\delta(t-1) \\ &\frac{d T_{2}}{d t}=-a\left(T_{2}-T_{\infty}\right)-H(t-1)+H(t-2) \end{aligned}$$

  where $\delta(t)$ and $H(t)$ are the Dirac delta and Heaviside functions respectively, and $a$ is a positive constant.

  (i) Show that for $0 \leqslant t<1$

  $$T_{1}(t)=T_{2}(t)=T_{\infty}+\left(T_{0}-T_{\infty}\right) \mathrm{e}^{-a t}$$

  (ii) Determine the jump (discontinuity) condition for $T_{1}$ at $t=1$ and hence find $T_{1}(t)$ for $t>1$.

  (iii) Using continuity of $T_{2}(t)$ at $t=1$ show that for $1<t<2$

  $$T_{2}(t)=T_{\infty}-\frac{1}{a}+\mathrm{e}^{-a t}\left(T_{0}-T_{\infty}+\frac{1}{a} \mathrm{e}^{a}\right)$$

  (iv) Compute $T_{2}(t)$ for $t>2$ and show that for $t>2$

  $$T_{1}(t)-T_{2}(t)=\left(\frac{1}{a} \mathrm{e}^{a}-1-\frac{1}{a}\right) \mathrm{e}^{(1-t) a}$$

  (v) Find the time $t^{*}$, after $t=1$, at which $T_{1}=T_{2}$.

  comment

• 2.II.6A

  Differential Equations | Part IA, 2008

  The linear second-order differential equation

  $$\frac{d^{2} y}{d x^{2}}+p(x) \frac{d y}{d x}+q(x) y=0$$

  has linearly independent solutions $y_{1}(x)$ and $y_{2}(x)$. Define the Wronskian $W$ of $y_{1}(x)$ and $y_{2}(x)$.

  Suppose that $y_{1}(x)$ is known. Use the Wronskian to write down a first-order differential equation for $y_{2}(x)$. Hence express $y_{2}(x)$ in terms of $y_{1}(x)$ and $W$.

  Show further that $W$ satisfies the differential equation

  $$\frac{d W}{d x}+p(x) W=0$$

  Verify that $y_{1}(x)=x^{2}-2 x+1$ is a solution of

  $$(x-1)^{2} \frac{d^{2} y}{d x^{2}}+(x-1) \frac{d y}{d x}-4 y=0 .$$

  Compute the Wronskian and hence determine a second, linearly independent, solution of $(*)$.

  comment

• 2.II.7A

  Differential Equations | Part IA, 2008

  Find the first three non-zero terms in series solutions $y_{1}(x)$ and $y_{2}(x)$ for the differential equation

  $$x \frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}+4 x^{3} y=0$$

  that satisfy the boundary conditions

  $$\begin{aligned} &y_{1}(0)=a, \quad y_{1}^{\prime \prime}(0)=0, \\ &y_{2}(0)=0, \quad y_{2}^{\prime \prime}(0)=b, \end{aligned}$$

  where $a$ and $b$ are constants.

  Determine the value of $\alpha$ such that the change of variable $u=x^{\alpha}$ transforms $(*)$ into a differential equation with constant coefficients. Hence find the general solution of $(*)$.

  comment

• 2.II.8A

  Differential Equations | Part IA, 2008

  Consider the function

  $$f(x, y)=x^{2}+y^{2}-\frac{1}{2} x^{4}-b x^{2} y^{2}-\frac{1}{2} y^{4}$$

  where $b$ is a positive constant.

  Find the critical points of $f(x, y)$, assuming $b \neq 1$. Determine the type of each critical point and sketch contours of constant $f(x, y)$ in the two cases (i) $b<1$ and (ii) $b>1$.

  For $b=1$ describe the subset of the $(x, y)$ plane on which $f(x, y)$ attains its maximum value.

  comment

Dynamics

• 4.I.3B

  Dynamics | Part IA, 2008

  Two particles of masses $m_{1}$ and $m_{2}$ have position vectors $\mathbf{r}_{1}(t)$ and $\mathbf{r}_{2}(t)$ at time $t$. The particle of mass $m_{1}$ experiences a force $\mathbf{f}$ and the particle of mass $m_{2}$ experiences a force $-\mathbf{f}$. Show that the centre of mass moves at a constant velocity, and derive an equation of motion for the relative separation $\mathbf{r}=\mathbf{r}_{1}-\mathbf{r}_{2}$.

  Now suppose that $\mathbf{f}=-k \mathbf{r}$, where $k$ is a positive constant. The particles are initially at rest a distance $d$ apart. Calculate how long it takes before they collide.

  comment

• 4.I.4B

  Dynamics | Part IA, 2008

  A damped pendulum is described by the equation

  $$\ddot{x}+2 k \dot{x}+\omega^{2} \sin x=0,$$

  where $k$ and $\omega$ are real positive constants. Determine the location of all the equilibrium points of the system. Classify the equilibrium points in the two cases $k>\omega$ and $k<\omega$.

  comment

• 4.II.10B

  Dynamics | Part IA, 2008

  A body of mass $m$ moves in the gravitational field of a much larger spherical object of mass $M$ located at the origin. Starting from the equations of motion

  $$\begin{aligned} \ddot{r}-r \dot{\theta}^{2} &=-\frac{G M}{r^{2}}, \\ r \ddot{\theta}+2 \dot{r} \dot{\theta} &=0, \end{aligned}$$

  show that:

  (i) the body moves in an orbit of the form

  $$\frac{h^{2} u}{G M}=1+e \cos \left(\theta-\theta_{0}\right)$$

  where $u=1 / r, h$ is the constant angular momentum per unit mass, and $e$ and $\theta_{0}$ are constants;

  (ii) the total energy of the body is

  $$E=\frac{m G^{2} M^{2}}{2 h^{2}}\left(e^{2}-1\right)$$

  A meteorite is moving very far from the Earth with speed $V$, and in the absence of the effect of the Earth's gravitational field would miss the Earth by a shortest distance $b$ (measured from the Earth's centre). Show that in the subsequent motion

  $$h=b V$$

  and

  $$e=\left[1+\frac{b^{2} V^{4}}{G^{2} M^{2}}\right]^{\frac{1}{2}}$$

  Use equation $(*)$ to find the distance of closest approach, and show that the meteorite will collide with the Earth if

  $$b<\left[R^{2}+\frac{2 G M R}{V^{2}}\right]^{\frac{1}{2}}$$

  where $R$ is the radius of the Earth.

  comment

• 4.II.11B

  Dynamics | Part IA, 2008

  An inertial reference frame $S$ and another reference frame $S^{\prime}$ have a common origin $O$, and $S^{\prime}$ rotates with angular velocity $\boldsymbol{\omega}(t)$ with respect to $S$. Show the following:

  (i) the rates of change of an arbitrary vector a $(t)$ in frames $S$ and $S^{\prime}$ are related by

  $$\left(\frac{d \mathbf{a}}{d t}\right)_{S}=\left(\frac{d \mathbf{a}}{d t}\right)_{S^{\prime}}+\boldsymbol{\omega} \times \mathbf{a}$$

  (ii) the accelerations in $S$ and $S^{\prime}$ are related by

  $$\left(\frac{d^{2} \mathbf{r}}{d t^{2}}\right)_{S}=\left(\frac{d^{2} \mathbf{r}}{d t^{2}}\right)_{S^{\prime}}+2 \boldsymbol{\omega} \times\left(\frac{d \mathbf{r}}{d t}\right)_{S^{\prime}}+\left(\frac{d \boldsymbol{\omega}}{d t}\right)_{S^{\prime}} \times \mathbf{r}+\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r})$$

  where $\mathbf{r}(t)$ is the position vector relative to $O$.

  A train of mass $m$ at latitude $\lambda$ in the Northern hemisphere travels North with constant speed $V$ along a track which runs North-South. Find the magnitude and direction of the sideways force exerted on the train by the track.

  comment

• 4.II.12B

  Dynamics | Part IA, 2008

  A uniform solid sphere has mass $m$ and radius $R_{0}$. Calculate the moment of inertia of the sphere about an axis through its centre.

  A long hollow circular cylinder of radius $R_{1}$ (where $R_{1}>2 R_{0}$ ) is held fixed with its axis horizontal. The sphere is held initially at rest in contact with the inner surface of the cylinder at $\theta=\alpha$, where $\alpha<\pi / 2$ and $\theta$ is the angle between the line joining the centre of the sphere to the cylinder axis and the downward vertical, as shown in the figure.

  

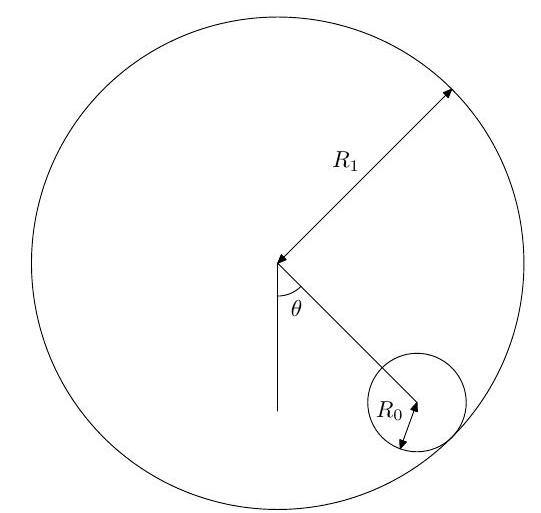
  The sphere is then released, and rolls without slipping. Show that the angular velocity of the sphere is

  $$\left(\frac{R_{1}-R_{0}}{R_{0}}\right) \dot{\theta} .$$

  Show further that the time, $T_{R}$, it takes the sphere to reach $\theta=0$ is

  $$T_{R}=\sqrt{\frac{7\left(R_{1}-R_{0}\right)}{10 g}} \quad \int_{0}^{\alpha} \frac{d \theta}{(\cos \theta-\cos \alpha)^{\frac{1}{2}}}$$

  If, instead, the cylinder and sphere surfaces are highly polished, so that the sphere now slides without rolling, find the time, $T_{S}$, it takes to reach $\theta=0$.

  Without further calculation, explain qualitatively how your answers for $T_{R}$ and $T_{S}$ would be affected if the solid sphere were replaced by a hollow spherical shell of the same radius and mass.

  comment

• 4.II.9B

  Dynamics | Part IA, 2008

  An octopus of mass $m_{o}$ swims horizontally in a straight line by jet propulsion. At time $t=0$ the octopus is at rest, and its internal cavity contains a mass $m_{w}$ of water (so that the mass of the octopus plus water is $m_{o}+m_{w}$ ). It then starts to move by ejecting the water backwards at a constant rate $Q$ units of mass per unit time and at a constant speed $V$ relative to itself. The speed of the octopus at time $t$ is $u(t)$, and the mass of the octopus plus remaining water is $m(t)$. The drag force exerted by the surrounding water on the octopus is $\alpha u^{2}$, where $\alpha$ is a positive constant.

  Show that, during ejection of water, the equation of motion is

  $$m \frac{d u}{d t}=Q V-\alpha u^{2} .$$

  Once all the water has been ejected, at time $t=t_{c}$, the octopus has attained a velocity $u_{c}$. Use dimensional analysis to show that

  $$u_{c}=V f(\lambda, \mu)$$

  where $\lambda$ and $\mu$ are two dimensionless quantities and $f$ is an unknown function. Solve equation (1) to find an explicit expression for $u_{c}$, and verify that your answer is of the form given in equation (2).

  comment

Groups

• $3 . \mathrm{II} . 6 \mathrm{E} \quad$

  Groups | Part IA, 2008

  Prove that two elements of $S_{n}$ are conjugate if and only if they have the same cycle type.

  Describe (without proof) a necessary and sufficient condition for a permutation $\sigma \in A_{n}$ to have the same conjugacy class in $A_{n}$ as it has in $S_{n}$.

  For which $\sigma \in S_{n}$ is $\sigma$ conjugate (in $S_{n}$ ) to $\sigma^{2} ?$

  For every $\sigma \in A_{5}$, show that $\sigma$ is conjugate to $\sigma^{-1}$ (in $\left.A_{5}\right)$. Exhibit a positive integer $n$ and a $\sigma \in A_{n}$ such that $\sigma$ is not conjugate to $\sigma^{-1}$ (in $A_{n}$ ).

  comment

• 3.I.1E

  Groups | Part IA, 2008

  Define the signature $\epsilon(\sigma)$ of a permutation $\sigma \in S_{n}$, and show that the map $\epsilon: S_{n} \rightarrow\{-1,1\}$ is a homomorphism.

  Define the alternating group $A_{n}$, and prove that it is a subgroup of $S_{n}$. Is $A_{n}$ a normal subgroup of $S_{n}$ ? Justify your answer.

  comment

• 3.I.2E

  Groups | Part IA, 2008

  What is the orthogonal group $O(n)$ ? What is the special orthogonal group $S O(n) ?$

  Show that every element of the special orthogonal group $S O(3)$ has an eigenvector with eigenvalue 1 . Is this also true for every element of the orthogonal group $O(3)$ ? Justify your answer.

  comment

• 3.II $. 5 \mathrm{E} \quad$

  Groups | Part IA, 2008

  For a normal subgroup $H$ of a group $G$, explain carefully how to make the set of (left) cosets of $H$ into a group.

  For a subgroup $H$ of a group $G$, show that the following are equivalent:

  (i) $H$ is a normal subgroup of $G$;

  (ii) there exist a group $K$ and a homomorphism $\theta: G \rightarrow K$ such that $H$ is the kernel of $\theta$.

  Let $G$ be a finite group that has a proper subgroup $H$ of index $n$ (in other words, $|H|=|G| / n)$. Show that if $|G|>n$ ! then $G$ cannot be simple. [Hint: Let $G$ act on the set of left cosets of $H$ by left multiplication.]

  comment

• 3.II $. 7 \mathrm{E} \quad$

  Groups | Part IA, 2008

  Show that every Möbius map may be expressed as a composition of maps of the form $z \mapsto z+a, z \mapsto \lambda z$ and $z \mapsto 1 / z$ (where $a$ and $\lambda$ are complex numbers).

  Which of the following statements are true and which are false? Justify your answers.

  (i) Every Möbius map that fixes $\infty$ may be expressed as a composition of maps of the form $z \mapsto z+a$ and $z \mapsto \lambda z$ (where $a$ and $\lambda$ are complex numbers).

  (ii) Every Möbius map that fixes 0 may be expressed as a composition of maps of the form $z \mapsto \lambda z$ and $z \mapsto 1 / z$ (where $\lambda$ is a complex number).

  (iii) Every Möbius map may be expressed as a composition of maps of the form $z \mapsto z+a$ and $z \mapsto 1 / z$ (where $a$ is a complex number).

  comment

• 3.II $. 8 \mathrm{E} \quad$

  Groups | Part IA, 2008

  State and prove the orbit-stabilizer theorem. Deduce that if $x$ is an element of a finite group $G$ then the order of $x$ divides the order of $G$

  Prove Cauchy's theorem, that if $p$ is a prime dividing the order of a finite group $G$ then $G$ contains an element of order $p$.

  For which positive integers $n$ does there exist a group of order $n$ in which every element (apart from the identity) has order 2?

  Give an example of an infinite group in which every element (apart from the identity) has order $2 .$

  comment

Numbers and Sets

• 4.I.1D

  Numbers and Sets | Part IA, 2008

  Let $A, B$ and $C$ be non-empty sets and let $f: A \rightarrow B$ and $g: B \rightarrow C$ be two functions. For each of the following statements, give either a brief justification or a counterexample.

  (i) If $f$ is an injection and $g$ is a surjection, then $g \circ f$ is a surjection.

  (ii) If $f$ is an injection and $g$ is an injection, then there exists a function $h: C \rightarrow A$ such that $h \circ g \circ f$ is equal to the identity function on $A$.

  (iii) If $X$ and $Y$ are subsets of $A$ then $f(X \cap Y)=f(X) \cap f(Y)$.

  (iv) If $Z$ and $W$ are subsets of $B$ then $f^{-1}(Z \cap W)=f^{-1}(Z) \cap f^{-1}(W)$.

  comment

• 4.I.2D

  Numbers and Sets | Part IA, 2008

  (a) Let $\sim$ be an equivalence relation on a set $X$. What is an equivalence class of $\sim ?$ Prove that the equivalence classes of $\sim$ form a partition of $X$.

  (b) Let $\mathbb{Z}^{+}$be the set of all positive integers. Let a relation $\sim$ be defined on $\mathbb{Z}^{+}$by setting $m \sim n$ if and only if $m / n=2^{k}$ for some (not necessarily positive) integer $k$. Prove that $\sim$ is an equivalence relation, and give an example of a set $A \subset \mathbb{Z}^{+}$that contains precisely one element of each equivalence class.

  comment

• 4.II.5D

  Numbers and Sets | Part IA, 2008

  (a) Define the notion of a countable set, and prove that the set $\mathbb{N} \times \mathbb{N}$ is countable. Deduce that if $X$ and $Y$ are countable sets then $X \times Y$ is countable, and also that a countable union of countable sets is countable.

  (b) If $A$ is any set of real numbers, define $\phi(A)$ to be the set of all real roots of non-zero polynomials that have coefficients in $A$. Now suppose that $A_{0}$ is a countable set of real numbers and define a sequence $A_{1}, A_{2}, A_{3}, \ldots$ by letting each $A_{n}$ be equal to $\phi\left(A_{n-1}\right)$. Prove that the union $\bigcup_{n=1}^{\infty} A_{n}$ is countable.

  (c) Deduce that there is a countable set $X$ that contains the real numbers 1 and $\pi$ and has the further property that if $P$ is any non-zero polynomial with coefficients in $X$, then all real roots of $P$ belong to $X$.

  comment

• 4.II.6D

  Numbers and Sets | Part IA, 2008

  (a) Let $a$ and $m$ be integers with $1 \leqslant a<m$ and let $d=(a, m)$ be their highest common factor. For any integer $b$, prove that $b$ is a multiple of $d$ if and only if there exists an integer $r$ satisfying the equation $a r \equiv b \operatorname{(\operatorname {mod}m)\text {,andshowthatinthiscasethereare}}$ exactly $d$ solutions to the equation that are distinct $\bmod m$.

  Deduce that the equation $a r \equiv b(\bmod m)$ has a solution if and only if $b(m / d) \equiv 0$ $(\bmod m)$.

  (b) Let $p$ be a prime and let $\mathbb{Z}_{p}^{*}$ be the multiplicative group of non-zero integers $\bmod p$. An element $x$ of $\mathbb{Z}_{p}^{*}$ is called a $k$ th power $(\bmod p)$ if $x \equiv y^{k}(\bmod p)$ for some integer $y$. It can be shown that $\mathbb{Z}_{p}^{*}$ has a generator: that is, an element $u$ such that every element of $\mathbb{Z}_{p}^{*}$ is a power of $u$. Assuming this result, deduce that an element $x$ of $\mathbb{Z}_{p}^{*}$ is a $k$ th power $(\bmod p)$ if and only if $x^{(p-1) / d} \equiv 1(\bmod p)$, where $d$ is now the highest common factor of $k$ and $p-1$.

  (c) How many 437th powers are there mod 1013? [You may assume that 1013 is a prime number.]

  comment

• 4.II.7D

  Numbers and Sets | Part IA, 2008

  (a) Let $\mathbb{F}$ be a field such that the equation $x^{2}=-1$ has no solution in $\mathbb{F}$. Prove that if $x$ and $y$ are elements of $\mathbb{F}$ such that $x^{2}+y^{2}=0$, then both $x$ and $y$ must equal 0 .

  Prove that $\mathbb{F}^{2}$ can be made into a field, with operations

  $$(x, y)+(z, w)=(x+z, y+w)$$

  and

  $$(x, y) \cdot(z, w)=(x z-y w, x w+y z) .$$

  (b) Let $p$ be a prime of the form $4 m+3$. Prove that $-1$ is not a square $(\bmod p)$, and deduce that there exists a field with exactly $p^{2}$ elements.

  comment

• 4.II.8D

  Numbers and Sets | Part IA, 2008

  Let $q$ be a positive integer. For every positive integer $k$, define a number $c_{k}$ by the formula

  $$c_{k}=(q+k-1) \frac{q !}{(q+k) !}$$

  Prove by induction that

  $$\sum_{k=1}^{n} c_{k}=1-\frac{q !}{(q+n) !}$$

  for every $n \geqslant 1$, and hence evaluate the infinite $\operatorname{sum} \sum_{k=1}^{\infty} c_{k}$.

  Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of integers satisfying the inequality $0 \leqslant a_{n}<n$ for every $n$. Prove that the series $\sum_{n=1}^{\infty} a_{n} / n$ ! is convergent. Prove also that its limit is irrational if and only if $a_{n} \leqslant n-2$ for infinitely many $n$ and $a_{m}>0$ for infinitely many $m$.

  comment

Probability

• 2.I.3F

  Probability | Part IA, 2008

  There are $n$ socks in a drawer, three of which are red and the rest black. John chooses his socks by selecting two at random from the drawer and puts them on. He is three times more likely to wear socks of different colours than to wear matching red socks. Find $n$.

  For this value of $n$, what is the probability that John wears matching black socks?

  comment

• 2.I.4F

  Probability | Part IA, 2008

  A standard six-sided die is thrown. Calculate the mean and variance of the number shown.

  The die is thrown $n$ times. By using Chebyshev's inequality, find an $n$ such that

  $$\mathbb{P}\left(\left|\frac{Y_{n}}{n}-3.5\right|>1.5\right) \leqslant 0.1$$

  where $Y_{n}$ is the total of the numbers shown over the $n$ throws.

  comment

• 2.II.10F

  Probability | Part IA, 2008

  $A$ and $B$ play a series of games. The games are independent, and each is won by $A$ with probability $p$ and by $B$ with probability $1-p$. The players stop when the number of wins by one player is three greater than the number of wins by the other player. The player with the greater number of wins is then declared overall winner.

  (i) Find the probability that exactly 5 games are played.

  (ii) Find the probability that $A$ is the overall winner.

  comment

• 2.II.11F

  Probability | Part IA, 2008

  Let $X$ and $Y$ have the bivariate normal density function

  $$f(x, y)=\frac{1}{2 \pi \sqrt{1-\rho^{2}}} \exp \left\{-\frac{1}{2\left(1-\rho^{2}\right)}\left(x^{2}-2 \rho x y+y^{2}\right)\right\}, \quad x, y \in \mathbb{R},$$

  for fixed $\rho \in(-1,1)$. Let $Z=(Y-\rho X) / \sqrt{1-\rho^{2}}$. Show that $X$ and $Z$ are independent $N(0,1)$ variables. Hence, or otherwise, determine

  $$\mathbb{P}(X>0, Y>0) .$$

  comment

• 2.II.12F

  Probability | Part IA, 2008

  The discrete random variable $Y$ has distribution given by

  $$\mathbb{P}(Y=k)=(1-p)^{k-1} p, \quad k=1,2, \ldots$$

  where $p \in(0,1)$. Determine the mean and variance of $Y$.

  A fair die is rolled until all 6 scores have occurred. Find the mean and standard deviation of the number of rolls required.

  [Hint: $\left.\sum_{i=1}^{6}\left(\frac{6}{i}\right)^{2}=53.7\right]$

  comment

• 2.II.9F

  Probability | Part IA, 2008

  A population evolves in generations. Let $Z_{n}$ be the number of members in the $n$th generation, with $Z_{0}=1$. Each member of the $n$th generation gives birth to a family, possibly empty, of members of the $(n+1)$ th generation; the size of this family is a random variable and we assume that the family sizes of all individuals form a collection of independent identically distributed random variables each with generating function $G$.

  Let $G_{n}$ be the generating function of $Z_{n}$. State and prove a formula for $G_{n}$ in terms of $G$. Determine the mean of $Z_{n}$ in terms of the mean of $Z_{1}$.

  Suppose that $Z_{1}$ has a Poisson distribution with mean $\lambda$. Find an expression for $x_{n+1}$ in terms of $x_{n}$, where $x_{n}=\mathbb{P}\left\{Z_{n}=0\right\}$ is the probability that the population becomes extinct by the $n$th generation.

  comment

Vector Calculus

• 3.I.3C

  Vector Calculus | Part IA, 2008

  A curve is given in terms of a parameter $t$ by

  $$\mathbf{x}(t)=\left(t-\frac{1}{3} t^{3}, t^{2}, t+\frac{1}{3} t^{3}\right)$$

  (i) Find the arc length of the curve between the points with $t=0$ and $t=1$.

  (ii) Find the unit tangent vector at the point with parameter $t$, and show that the principal normal is orthogonal to the $z$ direction at each point on the curve.

  comment

• 3.I.4C

  Vector Calculus | Part IA, 2008

  What does it mean to say that $T_{i j}$ transforms as a second rank tensor?

  If $T_{i j}$ transforms as a second rank tensor, show that $\frac{\partial T_{i j}}{\partial x_{j}}$ transforms as a vector.

  comment

• 3.II.10C

  Vector Calculus | Part IA, 2008

  Find the effect of a rotation by $\pi / 2$ about the $z$-axis on the tensor

  $$\left(\begin{array}{lll} S_{11} & S_{12} & S_{13} \\ S_{21} & S_{22} & S_{23} \\ S_{31} & S_{32} & S_{33} \end{array}\right)$$

  Hence show that the most general isotropic tensor of rank 2 is $\lambda \delta_{i j}$, where $\lambda$ is an arbitrary scalar.

  Prove that there is no non-zero isotropic vector, and write down without proof the most general isotropic tensor of rank 3 .

  Deduce that if $T_{i j k l}$ is an isotropic tensor then the following results hold, for some scalars $\mu$ and $\nu$ : (i) $\epsilon_{i j k} T_{i j k l}=0$; (ii) $\delta_{i j} T_{i j k l}=\mu \delta_{k l}$; (iii) $\epsilon_{i j m} T_{i j k l}=\nu \epsilon_{k l m}$.

  Verify these three results in the case $T_{i j k l}=\alpha \delta_{i j} \delta_{k l}+\beta \delta_{i k} \delta_{j l}+\gamma \delta_{i l} \delta_{j k}$, expressing $\mu$ and $\nu$ in terms of $\alpha, \beta$ and $\gamma$.

  comment

• 3.II.11C

  Vector Calculus | Part IA, 2008

  Let $V$ be a volume in $\mathbb{R}^{3}$ bounded by a closed surface $S$.

  (a) Let $f$ and $g$ be twice differentiable scalar fields such that $f=1$ on $S$ and $\nabla^{2} g=0$ in $V$. Show that

  $$\int_{V} \nabla f \cdot \nabla g d V=0$$

  (b) Let $V$ be the sphere $|\mathbf{x}| \leqslant a$. Evaluate the integral

  $$\int_{V} \nabla u \cdot \nabla v d V$$

  in the cases where $u$ and $v$ are given in spherical polar coordinates by: (i) $u=r, \quad v=r \cos \theta$; (ii) $u=r / a, \quad v=r^{2} \cos ^{2} \theta$; (iii) $u=r / a, \quad v=1 / r$.

  Comment on your results in the light of part (a).

  comment

• 3.II.12C

  Vector Calculus | Part IA, 2008

  Let $A$ be the closed planar region given by

  $$y \leqslant x \leqslant 2 y, \quad \frac{1}{y} \leqslant x \leqslant \frac{2}{y} .$$

  (i) Evaluate by means of a suitable change of variables the integral

  $$\int_{A} \frac{x}{y} d x d y$$

  (ii) Let $C$ be the boundary of $A$. Evaluate the line integral

  $$\oint_{C} \frac{x^{2}}{2 y} d y-d x$$

  by integrating along each section of the boundary.

  (iii) Comment on your results.

  comment

• 3.II.9C

  Vector Calculus | Part IA, 2008

  Let $\mathbf{F}=\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{x})$, where $\mathbf{x}$ is the position vector and $\boldsymbol{\omega}$ is a uniform vector field.

  (i) Use the divergence theorem to evaluate the surface integral $\int_{S} \mathbf{F} \cdot d \mathbf{S}$, where $S$ is the closed surface of the cube with vertices $(\pm 1, \pm 1, \pm 1)$.

  (ii) Show that $\boldsymbol{\nabla} \times \mathbf{F}=0$. Show further that the scalar field $\phi$ given by

  $$\phi=\frac{1}{2}(\boldsymbol{\omega} \cdot \mathbf{x})^{2}-\frac{1}{2}(\boldsymbol{\omega} \cdot \boldsymbol{\omega})(\mathbf{x} \cdot \mathbf{x})$$

  satisfies $\mathbf{F}=\boldsymbol{\nabla} \phi$. Describe geometrically the surfaces of constant $\phi$.

  comment

Vectors and Matrices

• 1.I.1B

  Vectors and Matrices | Part IA, 2008

  State de Moivre's Theorem. By evaluating

  $$\sum_{r=1}^{n} e^{i r \theta}$$

  or otherwise, show that

  $$\sum_{r=1}^{n} \cos (r \theta)=\frac{\cos (n \theta)-\cos ((n+1) \theta)}{2(1-\cos \theta)}-\frac{1}{2}$$

  Hence show that

  $$\sum_{r=1}^{n} \cos \left(\frac{2 p \pi r}{n+1}\right)=-1$$

  where $p$ is an integer in the range $1 \leqslant p \leqslant n$.

  comment

• 1.I.2A

  Vectors and Matrices | Part IA, 2008

  Let $U$ be an $n \times n$ unitary matrix $\left(U^{\dagger} U=U U^{\dagger}=I\right)$. Suppose that $A$ and $B$ are $n \times n$ Hermitian matrices such that $U=A+i B$.

  Show that

  (i) $A$ and $B$ commute,

  (ii) $A^{2}+B^{2}=I$.

  Find $A$ and $B$ in terms of $U$ and $U^{\dagger}$, and hence show that $A$ and $B$ are uniquely determined for a given $U$.

  comment

• 1.II $. 5 B \quad$

  Vectors and Matrices | Part IA, 2008

  (a) Use suffix notation to prove that

  $$\mathbf{a} \times(\mathbf{b} \times \mathbf{c})=(\mathbf{a} \cdot \mathbf{c}) \mathbf{b}-(\mathbf{a} \cdot \mathbf{b}) \mathbf{c}$$

  Hence, or otherwise, expand (i) $(\mathbf{a} \times \mathbf{b}) \cdot(\mathbf{c} \times \mathbf{d})$, (ii) $(\mathbf{a} \times \mathbf{b}) \cdot[(\mathbf{b} \times \mathbf{c}) \times(\mathbf{c} \times \mathbf{a})]$.

  (b) Write down the equation of the line that passes through the point a and is parallel to the unit vector $\hat{\mathbf{t}}$.

  The lines $L_{1}$ and $L_{2}$ in three dimensions pass through $\mathbf{a}_{1}$ and $\mathbf{a}_{2}$ respectively and are parallel to the unit vectors $\hat{\mathbf{t}}_{1}$ and $\hat{\mathbf{t}}_{2}$ respectively. Show that a necessary condition for $L_{1}$ and $L_{2}$ to intersect is

  $$\left(\mathbf{a}_{1}-\mathbf{a}_{2}\right) \cdot\left(\hat{\mathbf{t}}_{1} \times \hat{\mathbf{t}}_{2}\right)=0$$

  Why is this condition not sufficient?

  In the case in which $L_{1}$ and $L_{2}$ are non-parallel and non-intersecting, find an expression for the shortest distance between them.

  comment

• 1.II $. 7 \mathrm{C} \quad$

  Vectors and Matrices | Part IA, 2008

  Prove that any $n$ orthonormal vectors in $\mathbb{R}^{n}$ form a basis for $\mathbb{R}^{n}$.

  Let $A$ be a real symmetric $n \times n$ matrix with $n$ orthonormal eigenvectors $\mathbf{e}_{i}$ and corresponding eigenvalues $\lambda_{i}$. Obtain coefficients $a_{i}$ such that

  $$\mathbf{x}=\sum_{i} a_{i} \mathbf{e}_{i}$$

  is a solution to the equation

  $$A \mathbf{x}-\mu \mathbf{x}=\mathbf{f},$$

  where $\mathbf{f}$ is a given vector and $\mu$ is a given scalar that is not an eigenvalue of $A$.

  How would your answer differ if $\mu=\lambda_{1}$ ?

  Find $a_{i}$ and hence $\mathbf{x}$ when

  $$A=\left(\begin{array}{ccc} 2 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 3 \end{array}\right) \quad \text { and } \quad \mathbf{f}=\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right)$$

  in the cases (i) $\mu=2$ and (ii) $\mu=1$.

  comment

• 1.II.6A

  Vectors and Matrices | Part IA, 2008

  A real $3 \times 3$ matrix $A$ with elements $A_{i j}$ is said to be upper triangular if $A_{i j}=0$ whenever $i>j$. Prove that if $A$ and $B$ are upper triangular $3 \times 3$ real matrices then so is the matrix product $A B$.

  Consider the matrix

  $$A=\left(\begin{array}{rrr} 1 & 2 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & -1 \end{array}\right)$$

  Show that $A^{3}+A^{2}-A=I$. Write $A^{-1}$ as a linear combination of $A^{2}, A$ and $I$ and hence compute $A^{-1}$ explicitly.

  For all integers $n$ (including negative integers), prove that there exist coefficients $\alpha_{n}, \beta_{n}$ and $\gamma_{n}$ such that

  $$A^{n}=\alpha_{n} A^{2}+\beta_{n} A+\gamma_{n} I$$

  For all integers $n$ (including negative integers), show that

  $$\left(A^{n}\right)_{11}=1, \quad\left(A^{n}\right)_{22}=(-1)^{n}, \quad \text { and } \quad\left(A^{n}\right)_{23}=n(-1)^{n-1}$$

  Hence derive a set of 3 simultaneous equations for $\left\{\alpha_{n}, \beta_{n}, \gamma_{n}\right\}$ and find their solution.

  comment

• 1.II.8C

  Vectors and Matrices | Part IA, 2008

  Prove that the eigenvalues of a Hermitian matrix are real and that eigenvectors corresponding to distinct eigenvalues are orthogonal (i.e. $\mathbf{e}_{i}^{*} \cdot \mathbf{e}_{j}=0$ ).

  Let $A$ be a real $3 \times 3$ non-zero antisymmetric matrix. Show that $i A$ is Hermitian. Hence show that there exists a (complex) eigenvector $\mathbf{e}_{1}$ such $A \mathbf{e}_{1}=\lambda \mathbf{e}_{1}$, where $\lambda$ is imaginary.

  Show further that there exist real vectors $\mathbf{u}$ and $\mathbf{v}$ and a real number $\theta$ such that

  $$A \mathbf{u}=\theta \mathbf{v} \quad \text { and } \quad A \mathbf{v}=-\theta \mathbf{u}$$

  Show also that $A$ has a real eigenvector $\mathbf{e}_{3}$ such that $A \mathbf{e}_{3}=0$.

  Let $R=I+\sum_{n=1}^{\infty} \frac{A^{n}}{n !}$. By considering the action of $R$ on $\mathbf{u}, \mathbf{v}$ and $\mathbf{e}_{3}$, show that $R$ is a rotation matrix.

  comment