Part II, 2020, Paper 2

Algebraic Geometry

• Paper 2, Section II, F

  Algebraic Geometry | Part II, 2020

  Let $k$ be an algebraically closed field of characteristic not equal to 2 and let $V \subset \mathbb{P}_{k}^{3}$ be a nonsingular quadric surface.

  (a) Prove that $V$ is birational to $\mathbb{P}_{k}^{2}$.

  (b) Prove that there exists a pair of disjoint lines on $V$.

  (c) Prove that the affine variety $W=\mathbb{V}(x y z-1) \subset \mathbb{A}_{k}^{3}$ does not contain any lines.

  comment

Algebraic Topology

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2020

  (a) Let $f: X \rightarrow Y$ be a map of spaces. We define the mapping cylinder $M_{f}$ of $f$ to be the space

  $$(([0,1] \times X) \sqcup Y) / \sim$$

  with $(0, x) \sim f(x)$. Show carefully that the canonical inclusion $Y \hookrightarrow M_{f}$ is a homotopy equivalence.

  (b) Using the Seifert-van Kampen theorem, show that if $X$ is path-connected and $\alpha: S^{1} \rightarrow X$ is a map, and $x_{0}=\alpha\left(\theta_{0}\right)$ for some point $\theta_{0} \in S^{1}$, then

  $$\pi_{1}\left(X \cup_{\alpha} D^{2}, x_{0}\right) \cong \pi_{1}\left(X, x_{0}\right) /\langle\langle[\alpha]\rangle\rangle$$

  Use this fact to construct a connected space $X$ with

  $$\pi_{1}(X) \cong\left\langle a, b \mid a^{3}=b^{7}\right\rangle$$

  (c) Using a covering space of $S^{1} \vee S^{1}$, give explicit generators of a subgroup of $F_{2}$ isomorphic to $F_{3}$. Here $F_{n}$ denotes the free group on $n$ generators.

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, $35 \mathrm{C}$

  Applications of Quantum Mechanics | Part II, 2020

  a) Consider a particle moving in one dimension subject to a periodic potential, $V(x)=V(x+a)$. Define the Brillouin zone. State and prove Bloch's theorem.

  b) Consider now the following periodic potential

  $$V=V_{0}(\cos (x)-\cos (2 x))$$

  with positive constant $V_{0}$.

  i) For very small $V_{0}$, use the nearly-free electron model to compute explicitly the lowest-energy band gap to leading order in degenerate perturbation theory.

  ii) For very large $V_{0}$, the electron is localised very close to a minimum of the potential. Estimate the two lowest energies for such localised eigenstates and use the tight-binding model to estimate the lowest-energy band gap.

  comment

Applied Probability

• Paper 2, Section II, 27K

  Applied Probability | Part II, 2020

  (i) Let $X$ be a Markov chain in continuous time on the integers $\mathbb{Z}$ with generator $\mathbf{G}=\left(g_{i, j}\right)$. Define the corresponding jump chain $Y$.

  Define the terms irreducibility and recurrence for $X$. If $X$ is irreducible, show that $X$ is recurrent if and only if $Y$ is recurrent.

  (ii) Suppose

  $$g_{i, i-1}=3^{|i|}, \quad g_{i, i}=-3^{|i|+1}, \quad g_{i, i+1}=2 \cdot 3^{|i|}, \quad i \in \mathbb{Z} .$$

  Show that $X$ is transient, find an invariant distribution, and show that $X$ is explosive. [Any general results may be used without proof but should be stated clearly.]

  comment

Asymptotic Methods

• Paper 2, Section II, D

  Asymptotic Methods | Part II, 2020

  (a) Let $\delta>0$ and $x_{0} \in \mathbb{R}$. Let $\left\{\phi_{n}(x)\right\}_{n=0}^{\infty}$ be a sequence of (real) functions that are nonzero for all $x$ with $0<\left|x-x_{0}\right|<\delta$, and let $\left\{a_{n}\right\}_{n=0}^{\infty}$ be a sequence of nonzero real numbers. For every $N=0,1,2, \ldots$, the function $f(x)$ satisfies

  $$f(x)-\sum_{n=0}^{N} a_{n} \phi_{n}(x)=o\left(\phi_{N}(x)\right), \quad \text { as } \quad x \rightarrow x_{0}$$

  (i) Show that $\phi_{n+1}(x)=o\left(\phi_{n}(x)\right)$, for all $n=0,1,2, \ldots$; i.e., $\left\{\phi_{n}(x)\right\}_{n=0}^{\infty}$ is an asymptotic sequence.

  (ii) Show that for any $N=0,1,2, \ldots$, the functions $\phi_{0}(x), \phi_{1}(x), \ldots, \phi_{N}(x)$ are linearly independent on their domain of definition.

  (b) Let

  $$I(\varepsilon)=\int_{0}^{\infty}(1+\varepsilon t)^{-2} e^{-(1+\varepsilon) t} d t, \quad \text { for } \varepsilon>0$$

  (i) Find an asymptotic expansion (not necessarily a power series) of $I(\varepsilon)$, as $\varepsilon \rightarrow 0^{+}$.

  (ii) Find the first four terms of the expansion of $I(\varepsilon)$ into an asymptotic power series of $\varepsilon$, that is, with error $o\left(\varepsilon^{3}\right)$ as $\varepsilon \rightarrow 0^{+}$.

  comment

Automata and Formal Languages

• Paper 2, Section I, F

  Automata and Formal Languages | Part II, 2020

  Assuming the definition of a partial recursive function from $\mathbb{N}$ to $\mathbb{N}$, what is a recursive subset of $\mathbb{N}$ ? What is a recursively enumerable subset of $\mathbb{N}$ ?

  Show that a subset $E \subseteq \mathbb{N}$ is recursive if and only if $E$ and $\mathbb{N} \backslash E$ are recursively enumerable.

  Are the following subsets of $\mathbb{N}$ recursive?

  (i) $\mathbb{K}:=\left\{n \mid n\right.$ codes a program and $f_{n, 1}(n)$ halts at some stage $\}$.

  (ii) $\mathbb{K}_{100}:=\left\{n \mid n\right.$ codes a program and $f_{n, 1}(n)$ halts within 100 steps $\}$.

  comment

Classical Dynamics

• Paper 2, Section I, B

  Classical Dynamics | Part II, 2020

  A particle of mass $m$ has position vector $\mathbf{r}(t)$ in a frame of reference that rotates with angular velocity $\boldsymbol{\omega}(t)$. The particle moves under the gravitational influence of masses that are fixed in the rotating frame. Explain why the Lagrangian of the particle is of the form

  $$L=\frac{1}{2} m(\dot{\mathbf{r}}+\boldsymbol{\omega} \times \mathbf{r})^{2}-V(\mathbf{r}) .$$

  Show that Lagrange's equations of motion are equivalent to

  $$m(\ddot{\mathbf{r}}+2 \boldsymbol{\omega} \times \dot{\mathbf{r}}+\dot{\boldsymbol{\omega}} \times \mathbf{r}+\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r}))=-\boldsymbol{\nabla} V$$

  Identify the canonical momentum $\mathbf{p}$ conjugate to $\mathbf{r}$. Obtain the Hamiltonian $H(\mathbf{r}, \mathbf{p})$ and Hamilton's equations for this system.

  comment

• Paper 2, Section II, B

  Classical Dynamics | Part II, 2020

  A symmetric top of mass $M$ rotates about a fixed point that is a distance $l$ from the centre of mass along the axis of symmetry; its principal moments of inertia about the fixed point are $I_{1}=I_{2}$ and $I_{3}$. The Lagrangian of the top is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  (i) Draw a diagram explaining the meaning of the Euler angles $\theta, \phi$ and $\psi$.

  (ii) Derive expressions for the three integrals of motion $E, L_{3}$ and $L_{z}$.

  (iii) Show that the nutational motion is governed by the equation

  $$\frac{1}{2} I_{1} \dot{\theta}^{2}+V_{\text {eff }}(\theta)=E^{\prime}$$

  and derive expressions for the effective potential $V_{\mathrm{eff}}(\theta)$ and the modified energy $E^{\prime}$ in terms of $E, L_{3}$ and $L_{z}$.

  (iv) Suppose that

  $$L_{z}=L_{3}\left(1-\frac{\epsilon^{2}}{2}\right)$$

  where $\epsilon$ is a small positive number. By expanding $V_{\text {eff }}$ to second order in $\epsilon$ and $\theta$, show that there is a stable equilibrium solution with $\theta=O(\epsilon)$, provided that $L_{3}^{2}>4 M g l I_{1}$. Determine the equilibrium value of $\theta$ and the precession rate $\dot{\phi}$, to the same level of approximation.

  comment

Coding and Cryptography

• Paper 2, Section I, I

  Coding and Cryptography | Part II, 2020

  (a) Define the information capacity of a discrete memoryless channel (DMC).

  (b) Consider a DMC where there are two input symbols, $A$ and $B$, and three output symbols, $A, B$ and $\star$. Suppose each input symbol is left intact with probability $1 / 2$, and transformed into a $\star$ with probability $1 / 2$.

  (i) Write down the channel matrix, and calculate the information capacity.

  (ii) Now suppose the output is further processed by someone who cannot distinguish between $A$ and $\star$, so that the channel matrix becomes

  $$\left(\begin{array}{cc} 1 & 0 \\ 1 / 2 & 1 / 2 \end{array}\right)$$

  Calculate the new information capacity.

  comment

• Paper 2, Section II, I

  Coding and Cryptography | Part II, 2020

  Let $C$ be the Hamming $(n, n-d)$ code of weight 3 , where $n=2^{d}-1, d>1$. Let $H$ be the parity-check matrix of $C$. Let $\nu(j)$ be the number of codewords of weight $j$ in $C$.

  (i) Show that for any two columns $h_{1}$ and $h_{2}$ of $H$ there exists a unique third column $h_{3}$ such that $h_{3}=h_{2}+h_{1}$. Deduce that $\nu(3)=n(n-1) / 6$.

  (ii) Show that $C$ contains a codeword of weight $n$.

  (iii) Find formulae for $\nu(n-1), \nu(n-2)$ and $\nu(n-3)$. Justify your answer in each case.

  comment

Cosmology

• Paper 2, Section I, D

  Cosmology | Part II, 2020

  During inflation, the expansion of the universe is governed by the Friedmann equation,

  $$H^{2}=\frac{8 \pi G}{3 c^{2}}\left(\frac{1}{2} \dot{\phi}^{2}+V(\phi)\right)$$

  and the equation of motion for the inflaton field $\phi$,

  $$\ddot{\phi}+3 H \dot{\phi}+\frac{\partial V}{\partial \phi}=0 \text {. }$$

  The slow-roll conditions are $\dot{\phi}^{2} \ll V(\phi)$ and $\ddot{\phi} \ll H \dot{\phi}$. Under these assumptions, solve for $\phi(t)$ and $a(t)$ for the potentials:

  (i) $V(\phi)=\frac{1}{2} m^{2} \phi^{2}$ and

  (ii) $V(\phi)=\frac{1}{4} \lambda \phi^{4}, \quad(\lambda>0)$.

  comment

Differential Geometry

• Paper 2, Section II, I

  Differential Geometry | Part II, 2020

  (a) State the fundamental theorem for regular curves in $\mathbb{R}^{3}$.

  (b) Let $\alpha: \mathbb{R} \rightarrow \mathbb{R}^{3}$ be a regular curve, parameterised by arc length, such that its image $\alpha(\mathbb{R}) \subset \mathbb{R}^{3}$ is a one-dimensional submanifold. Suppose that the set $\alpha(\mathbb{R})$ is preserved by a nontrivial proper Euclidean motion $\phi: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$.

  Show that there exists $\sigma_{0} \in \mathbb{R}$ corresponding to $\phi$ such that $\phi(\alpha(s))=\alpha\left(\pm s+\sigma_{0}\right)$ for all $s \in \mathbb{R}$, where the choice of $\pm \operatorname{sign}$ is independent of $s$. Show also that the curvature $k(s)$ and torsion $\tau(s)$ of $\alpha$ satisfy

  $$\begin{gathered} k\left(\pm s+\sigma_{0}\right)=k(s) \text { and } \\ \tau\left(\pm s+\sigma_{0}\right)=\tau(s) \end{gathered}$$

  with equation (2) valid only for $s$ such that $k(s)>0$. In the case where the sign is $+$ and $\sigma_{0}=0$, show that $\alpha(\mathbb{R})$ is a straight line.

  (c) Give an explicit example of a curve $\alpha$ satisfying the requirements of (b) such that neither of $k(s)$ and $\tau(s)$ is a constant function, and such that the curve $\alpha$ is closed, i.e. such that $\alpha(s)=\alpha\left(s+s_{0}\right)$ for some $s_{0}>0$ and all $s$. [Here a drawing would suffice.]

  (d) Suppose now that $\alpha: \mathbb{R} \rightarrow \mathbb{R}^{3}$ is an embedded regular curve parameterised by arc length $s$. Suppose further that $k(s)>0$ for all $s$ and that $k(s)$ and $\tau(s)$ satisfy (1) and (2) for some $\sigma_{0}$, where the choice $\pm$ is independent of $s$, and where $\sigma_{0} \neq 0$ in the case of + sign. Show that there exists a nontrivial proper Euclidean motion $\phi$ such that the set $\alpha(\mathbb{R})$ is preserved by $\phi$. [You may use the theorem of part (a) without proof.]

  comment

Dynamical Systems

• Paper 2, Section II, E

  Dynamical Systems | Part II, 2020

  (a) State and prove Dulac's criterion. State clearly the Poincaré-Bendixson theorem.

  (b) For $(x, y) \in \mathbb{R}^{2}$ and $k>0$, consider the dynamical system

  $$\begin{aligned} &\dot{x}=k x-5 y-(3 x+y)\left(5 x^{2}-6 x y+5 y^{2}\right) \\ &\dot{y}=5 x+(k-6) y-(x+3 y)\left(5 x^{2}-6 x y+5 y^{2}\right) \end{aligned}$$

  (i) Use Dulac's criterion to find a range of $k$ for which this system does not have any periodic orbit.

  (ii) Find a suitable $f(k)>0$ such that trajectories enter the disc $x^{2}+y^{2} \leqslant f(k)$ and do not leave it.

  (iii) Given that the system has no fixed points apart from the origin for $k<10$, give a range of $k$ for which there will exist at least one periodic orbit.

  comment

Fluid Dynamics II

• Paper 2, Section II, 38B

  Fluid Dynamics II | Part II, 2020

  Consider a two-dimensional flow of a viscous fluid down a plane inclined at an angle $\alpha$ to the horizontal. Initially, the fluid, which has a volume $V$, occupies a region $0 \leqslant x \leqslant x^{*}$ with $x$ increasing down the slope. At large times the flow becomes thin-layer flow.

  (i) Write down the two-dimensional Navier-Stokes equations and simplify them using the lubrication approximation. Show that the governing equation for the height of the film, $h=h(x, t)$, is

  $$\tag{†} \frac{\partial h}{\partial t}+\frac{\partial}{\partial x}\left(\frac{g h^{3} \sin \alpha}{3 \nu}\right)=0$$

  where $\nu$ is the kinematic viscosity of the fluid and $g$ is the acceleration due to gravity, being careful to justify why the streamwise pressure gradient has been ignored compared to the gravitational body force.

  (ii) Develop a similarity solution to $(†)$ and, using the fact that the volume of fluid is conserved over time, derive an expression for the position and height of the head of the current downstream.

  (iii) Fluid is now continuously supplied at $x=0$. By using scaling analysis, estimate the rate at which fluid would have to be supplied for the head height to asymptote to a constant value at large times.

  comment

Further Complex Methods

• Paper 2, Section $I$, E

  Further Complex Methods | Part II, 2020

  Evaluate

  $$\int_{C} \frac{d z}{\sin ^{3} z}$$

  where $C$ is the circle $|z|=4$ traversed in the counter-clockwise direction.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2020

  A semi-infinite elastic string is initially at rest on the $x$-axis with $0 \leqslant x<\infty$. The transverse displacement of the string, $y(x, t)$, is governed by the partial differential equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  where $c$ is a positive real constant. For $t \geqslant 0$ the string is subject to the boundary conditions $y(0, t)=f(t)$ and $y(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (i) Show that the Laplace transform of $y(x, t)$ takes the form

  $$\hat{y}(x, p)=\hat{f}(p) e^{-p x / c}$$

  (ii) For $f(t)=\sin \omega t$, with $\omega \in \mathbb{R}^{+}$, find $\hat{f}(p)$ and hence write $\hat{y}(x, p)$ in terms of $\omega, c, p$ and $x$. Obtain $y(x, t)$ by performing the inverse Laplace transform using contour integration. Provide a physical interpretation of the result.

  comment

Galois Theory

• Paper 2, Section II, 18G

  Galois Theory | Part II, 2020

  (a) Let $K$ be a field and let $L$ be the splitting field of a polynomial $f(x) \in K[x]$. Let $\xi_{N}$ be a primitive $N^{\text {th }}$root of unity. Show that $\operatorname{Aut}\left(L\left(\xi_{N}\right) / K\left(\xi_{N}\right)\right)$ is a subgroup of $\operatorname{Aut}(L / K)$.

  (b) Suppose that $L / K$ is a Galois extension of fields with cyclic Galois group generated by an element $\sigma$ of order $d$, and that $K$ contains a primitive $d^{\text {th }}$root of unity $\xi_{d}$. Show that an eigenvector $\alpha$ for $\sigma$ on $L$ with eigenvalue $\xi_{d}$ generates $L / K$, that is, $L=K(\alpha)$. Show that $\alpha^{d} \in K$.

  (c) Let $G$ be a finite group. Define what it means for $G$ to be solvable.

  Determine whether

  (i) $G=S_{4} ; \quad$ (ii) $G=S_{5}$

  are solvable.

  (d) Let $K=\mathbb{Q}\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ be the field of fractions of the polynomial ring $\mathbb{Q}\left[a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right]$. Let $f(x)=x^{5}-a_{1} x^{4}+a_{2} x^{3}-a_{3} x^{2}+a_{4} x-a_{5} \in K[x]$. Show that $f$ is not solvable by radicals. [You may use results from the course provided that you state them clearly.]

  comment

General Relativity

• Paper 2, Section II, $37 \mathrm{D}$

  General Relativity | Part II, 2020

  The Schwarzschild metric is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2} d \theta^{2}+r^{2} \sin ^{2} \theta d \phi^{2}$$

  (i) Show that geodesics in the Schwarzschild spacetime obey the equation

  $$\frac{1}{2} \dot{r}^{2}+V(r)=\frac{1}{2} E^{2}, \quad \text { where } V(r)=\frac{1}{2}\left(1-\frac{2 M}{r}\right)\left(\frac{L^{2}}{r^{2}}-Q\right)$$

  where $E, L, Q$ are constants and the dot denotes differentiation with respect to a suitably chosen affine parameter $\lambda$.

  (ii) Consider the following three observers located in one and the same plane in the Schwarzschild spacetime which also passes through the centre of the black hole:

  • Observer $\mathcal{O}_{1}$ is on board a spacecraft (to be modeled as a pointlike object moving on a geodesic) on a circular orbit of radius $r>3 M$ around the central mass $M$.

  • Observer $\mathcal{O}_{2}$ starts at the same position as $\mathcal{O}_{1}$ but, instead of orbiting, stays fixed at the initial coordinate position by using rocket propulsion to counteract the gravitational pull.

  • Observer $\mathcal{O}_{3}$ is also located at a fixed position but at large distance $r \rightarrow \infty$ from the central mass and is assumed to be able to see $\mathcal{O}_{1}$ whenever the two are at the same azimuthal angle $\phi$.

  Show that the proper time intervals $\Delta \tau_{1}, \Delta \tau_{2}, \Delta \tau_{3}$, that are measured by the three observers during the completion of one full orbit of observer $\mathcal{O}_{1}$, are given by

  $$\Delta \tau_{i}=2 \pi \sqrt{\frac{r^{2}\left(r-\alpha_{i} M\right)}{M}}, \quad i=1,2,3$$

  where $\alpha_{1}, \alpha_{2}$ and $\alpha_{3}$ are numerical constants that you should determine.

  (iii) Briefly interpret the result by arranging the $\Delta \tau_{i}$ in ascending order.

  comment

Graph Theory

• Paper 2, Section II, 17G

  Graph Theory | Part II, 2020

  (i) Define the local connectivity $\kappa(a, b ; G)$ for two non-adjacent vertices $a$ and $b$ in a graph $G$. Prove Menger's theorem, that $G$ contains a set of $\kappa(a, b ; G)$ vertex-disjoint $a-b$ paths.

  (ii) Recall that a subdivision $T K_{r}$ of $K_{r}$ is any graph obtained from $K_{r}$ by replacing its edges by vertex-disjoint paths. Let $G$ be a 3 -connected graph. Show that $G$ contains a $T K_{3}$. Show further that $G$ contains a $T K_{4}$. Must $G$ contain a $T K_{5}$?

  comment

Integrable Systems

• Paper 2, Section II, 33C

  Integrable Systems | Part II, 2020

  (i) Explain how the inverse scattering method can be used to solve the initial value problem for the $\mathrm{KdV}$ equation

  $$u_{t}+u_{x x x}-6 u u_{x}=0, \quad u(x, 0)=u_{0}(x)$$

  including a description of the scattering data associated to the operator $L_{u}=-\partial_{x}^{2}+u(x, t)$, its time dependence, and the reconstruction of $u$ via the inverse scattering problem.

  (ii) Solve the inverse scattering problem for the reflectionless case, in which the reflection coefficient $R(k)$ is identically zero and the discrete scattering data consists of a single bound state, and hence derive the 1-soliton solution of $\mathrm{KdV}$.

  (iii) Consider the direct and inverse scattering problems in the case of a small potential $u(x)=\epsilon q(x)$, with $\epsilon$ arbitrarily small: $0<\epsilon \ll 1$. Show that the reflection coefficient is given by

  $$R(k)=\epsilon \int_{-\infty}^{\infty} \frac{e^{-2 i k z}}{2 i k} q(z) d z+O\left(\epsilon^{2}\right)$$

  and verify that the solution of the inverse scattering problem applied to this reflection coefficient does indeed lead back to the potential $u=\epsilon q$ when calculated to first order in

  

  comment

Linear Analysis

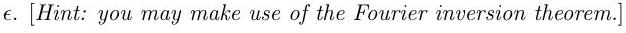
• Paper 2, Section II, I

  Linear Analysis | Part II, 2020

  (a) State and prove the Baire Category theorem.

  Let $p>1$. Apply the Baire Category theorem to show that $\bigcup_{1 \leqslant q<p} l_{q} \neq l_{p}$. Give an explicit element of $l_{p} \backslash \bigcup_{1 \leqslant q<p} l_{q}$.

  (b) Use the Baire Category theorem to prove that $C([0,1])$ contains a function which is nowhere differentiable.

  (c) Let $(X,\|\cdot\|)$ be a real Banach space. Verify that the map sending $x$ to the function $e_{x}: \phi \mapsto \phi(x)$ is a continuous linear map of $X$ into $\left(X^{*}\right)^{*}$ where $X^{*}$ denotes the dual space of $(X,\|\cdot\|)$. Taking for granted the fact that this map is an isometry regardless of the norm on $X$, prove that if $\|\cdot\|^{\prime}$ is another norm on the vector space $X$ which is not equivalent to $\|\cdot\|$, then there is a linear function $\psi: X \rightarrow \mathbb{R}$ which is continuous with respect to one of the two norms $\|\cdot\|,\|\cdot\|^{\prime}$ and not continuous with respect to the other.

  comment

Logic and Set Theory

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2020

  (a) This part of the question is concerned with propositional logic.

  Let $P$ be a set of primitive propositions. Let $S \subset L(P)$ be a consistent, deductively closed set such that for every $t \in L(P)$ either $t \in S$ or $\neg t \in S$. Show that $S$ has a model.

  (b) This part of the question is concerned with predicate logic.

  (i) State Gödel's completeness theorem for first-order logic. Deduce the compactness theorem, which you should state precisely.

  (ii) Let $X$ be an infinite set. For each $x \in X$, let $L_{x}$ be a subset of $X$. Suppose that for any finite $Y \subseteq X$ there exists a function $f_{Y}: Y \rightarrow\{1, \ldots, 100\}$ such that for all $x \in Y$ and all $y \in Y \cap L_{x}, f_{Y}(x) \neq f_{Y}(y)$. Show that there exists a function $F: X \rightarrow\{1, \ldots, 100\}$ such that for all $x \in X$ and all $y \in L_{x}, F(x) \neq F(y)$.

  comment

Mathematical Biology

• Paper 2, Section I, 6B

  Mathematical Biology | Part II, 2020

  Consider the system of predator-prey equations

  $$\begin{aligned} &\frac{d N_{1}}{d t}=-\epsilon_{1} N_{1}+\alpha N_{1} N_{2} \\ &\frac{d N_{2}}{d t}=\epsilon_{2} N_{2}-\alpha N_{1} N_{2} \end{aligned}$$

  where $\epsilon_{1}, \epsilon_{2}$ and $\alpha$ are positive constants.

  (i) Determine the non-zero fixed point $\left(N_{1}^{*}, N_{2}^{*}\right)$ of this system.

  (ii) Show that the system can be written in the form

  $$\frac{d x_{i}}{d t}=\sum_{j=1}^{2} K_{i j} \frac{\partial H}{\partial x_{j}}, \quad i=1,2$$

  where $x_{i}=\log \left(N_{i} / N_{i}^{*}\right)$ and a suitable $2 \times 2$ antisymmetric matrix $K_{i j}$ and scalar function $H\left(x_{1}, x_{2}\right)$ are to be identified.

  (iii) Hence, or otherwise, show that $H$ is constant on solutions of the predator-prey equations.

  comment

Mathematics of Machine Learning

• Paper 2, Section II, J

  Mathematics of Machine Learning | Part II, 2020

  (a) Let $\mathcal{F}$ be a family of functions $f: \mathcal{X} \rightarrow\{0,1\}$. What does it mean for $x_{1: n} \in \mathcal{X}^{n}$ to be shattered by $\mathcal{F}$ ? Define the shattering coefficient $s(\mathcal{F}, n)$ and the $V C$ dimension $\operatorname{VC}(\mathcal{F})$ of $\mathcal{F}$

  Let

  $$\mathcal{A}=\left\{\prod_{j=1}^{d}\left(-\infty, a_{j}\right]: a_{1}, \ldots, a_{d} \in \mathbb{R}\right\}$$

  and set $\mathcal{F}=\left\{\mathbf{1}_{A}: A \in \mathcal{A}\right\}$. Compute $\operatorname{VC}(\mathcal{F})$.

  (b) State the Sauer-Shelah lemma.

  (c) Let $\mathcal{F}_{1}, \ldots, \mathcal{F}_{r}$ be families of functions $f: \mathcal{X} \rightarrow\{0,1\}$ with finite VC dimension $v \geqslant 1$. Now suppose $x_{1: n}$ is shattered by $\cup_{k=1}^{r} \mathcal{F}_{k}$. Show that

  $$2^{n} \leqslant r(n+1)^{v} .$$

  Conclude that for $v \geqslant 3$,

  $$\mathrm{VC}\left(\cup_{k=1}^{r} \mathcal{F}_{k}\right) \leqslant 4 v \log _{2}(2 v)+2 \log _{2}(r)$$

  [You may use without proof the fact that if $x \leqslant \alpha+\beta \log _{2}(x+1)$ with $\alpha>0$ and $\beta \geqslant 3$, then $x \leqslant 4 \beta \log _{2}(2 \beta)+2 \alpha$ for $x \geqslant 1$.]

  (d) Now let $\mathcal{B}$ be the collection of subsets of $\mathbb{R}^{p}$ of the form of a product $\prod_{j=1}^{p} A_{j}$ of intervals $A_{j}$, where exactly $d \in\{1, \ldots, p\}$ of the $A_{j}$ are of the form $\left(-\infty, a_{j}\right]$ for $a_{j} \in \mathbb{R}$ and the remaining $p-d$ intervals are $\mathbb{R}$. Set $\mathcal{G}=\left\{\mathbf{1}_{B}: B \in \mathcal{B}\right\}$. Show that when $d \geqslant 3$,

  $$\mathrm{VC}(\mathcal{G}) \leqslant 2 d\left[2 \log _{2}(2 d)+\log _{2}(p)\right]$$

  comment

Number Fields

• Paper 2, Section II, 20G

  Number Fields | Part II, 2020

  (a) Let $K$ be a number field of degree $n$. Define the discriminant $\operatorname{disc}\left(\alpha_{1}, \ldots, \alpha_{n}\right)$ of an $n$-tuple of elements $\alpha_{i}$ of $K$, and show that it is nonzero if and only if $\alpha_{1}, \ldots, \alpha_{n}$ is a $\mathbb{Q}$-basis for $K$.

  (b) Let $K=\mathbb{Q}(\alpha)$ where $\alpha$ has minimal polynomial

  $$T^{n}+\sum_{j=0}^{n-1} a_{j} T^{j}, \quad a_{j} \in \mathbb{Z}$$

  and assume that $p$ is a prime such that, for every $j, a_{j} \equiv 0(\bmod p)$, but $a_{0} \not \equiv 0\left(\bmod p^{2}\right)$.

  (i) Show that $P=(p, \alpha)$ is a prime ideal, that $P^{n}=(p)$ and that $\alpha \notin P^{2}$. [Do not assume that $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$.]

  (ii) Show that the index of $\mathbb{Z}[\alpha]$ in $\mathcal{O}_{K}$ is prime to $p$.

  (iii) If $K=\mathbb{Q}(\alpha)$ with $\alpha^{3}+3 \alpha+3=0$, show that $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$. [You may assume without proof that the discriminant of $T^{3}+a T+b$ is $-4 a^{3}-27 b^{2}$.]

  comment

Number Theory

• Paper 2, Section I, $1 \mathbf{H}$

  Number Theory | Part II, 2020

  Let $\theta \in \mathbb{R}$.

  For each integer $n \geqslant-1$, define the convergents $p_{n} / q_{n}$ of the continued fraction expansion of $\theta$. Show that for all $n \geqslant 0, p_{n} q_{n-1}-p_{n-1} q_{n}=(-1)^{n-1}$. Deduce that if $q \in \mathbb{N}$ and $p \in \mathbb{Z}$ satisfy

  $$\left|\theta-\frac{p}{q}\right|<\left|\theta-\frac{p_{n}}{q_{n}}\right|$$

  then $q>q_{n}$.

  Compute the continued fraction expansion of $\sqrt{12}$. Hence or otherwise find a solution in positive integers $x$ and $y$ to the equation $x^{2}-12 y^{2}=1$.

  comment

Numerical Analysis

• Paper 2, Section II, 40E

  Numerical Analysis | Part II, 2020

  (a) For $A \in \mathbb{R}^{n \times n}$ and nonzero $\boldsymbol{v} \in \mathbb{R}^{n}$, define the $m$-th Krylov subspace $K_{m}(A, \boldsymbol{v})$ of $\mathbb{R}^{n}$. Prove that if $A$ has $n$ linearly independent eigenvectors with at most $s$ distinct eigenvalues, then

  $$\operatorname{dim} K_{m}(A, \boldsymbol{v}) \leqslant s \quad \forall m$$

  (b) Define the term residual in the conjugate gradient (CG) method for solving a system $A \boldsymbol{x}=\boldsymbol{b}$ with a symmetric positive definite $A$. State two properties of the method regarding residuals and their connection to certain Krylov subspaces, and hence show that, for any right-hand side $\boldsymbol{b}$, the method finds the exact solution after at most $s$ iterations, where $s$ is the number of distinct eigenvalues of $A$.

  (c) The preconditioned CG-method $P A P^{T} \widehat{\boldsymbol{x}}=P \boldsymbol{b}$ is applied for solving $A \boldsymbol{x}=\boldsymbol{b}$, with

  

  Prove that the method finds the exact solution after two iterations at most.

  (d) Prove that, for any symmetric positive definite $A$, we can find a preconditioner $P$ such that the preconditioned CG-method for solving $A \boldsymbol{x}=\boldsymbol{b}$ would require only one step. Explain why this preconditioning is of hardly any use.

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, A

  Principles of Quantum Mechanics | Part II, 2020

  (a) Consider the Hamiltonian $H(t)=H_{0}+\delta H(t)$, where $H_{0}$ is time-independent and non-degenerate. The system is prepared to be in some state $|\psi\rangle=\sum_{r} a_{r}|r\rangle$ at time $t=0$, where $\{|r\rangle\}$ is an orthonormal basis of eigenstates of $H_{0}$. Derive an expression for the state at time $t$, correct to first order in $\delta H(t)$, giving your answer in the interaction picture.

  (b) An atom is modelled as a two-state system, where the excited state $|e\rangle$ has energy $\hbar \Omega$ above that of the ground state $|g\rangle$. The atom interacts with an electromagnetic field, modelled as a harmonic oscillator of frequency $\omega$. The Hamiltonian is $H(t)=H_{0}+\delta H(t)$, where

  $$H_{0}=\frac{\hbar \Omega}{2}(|e\rangle\langle e|-| g\rangle\langle g|) \otimes 1_{\text {field }}+1_{\text {atom }} \otimes \hbar \omega\left(A^{\dagger} A+\frac{1}{2}\right)$$

  is the Hamiltonian in the absence of interactions and

  $$\delta H(t)= \begin{cases}0, & t \leqslant 0 \\ \frac{1}{2} \hbar(\Omega-\omega)\left(|e\rangle\langle g|\otimes A+\beta| g\rangle\langle e| \otimes A^{\dagger}\right), & t>0\end{cases}$$

  describes the coupling between the atom and the field.

  (i) Interpret each of the two terms in $\delta H(t)$. What value must the constant $\beta$ take for time evolution to be unitary?

  (ii) At $t=0$ the atom is in state $(|e\rangle+|g\rangle) / \sqrt{2}$ while the field is described by the (normalized) state $e^{-1 / 2} e^{-A^{\dagger}}|0\rangle$ of the oscillator. Calculate the probability that at time $t$ the atom will be in its excited state and the field will be described by the $n^{\text {th }}$excited state of the oscillator. Give your answer to first non-trivial order in perturbation theory. Show that this probability vanishes when $t=\pi /(\Omega-\omega)$.

  comment

Principles of Statistics

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2020

  Consider $X_{1}, \ldots, X_{n}$ from a $N\left(\mu, \sigma^{2}\right)$ distribution with parameter $\theta=\left(\mu, \sigma^{2}\right) \in$ $\Theta=\mathbb{R} \times(0, \infty)$. Derive the likelihood ratio test statistic $\Lambda_{n}\left(\Theta, \Theta_{0}\right)$ for the composite hypothesis

  $$H_{0}: \sigma^{2}=1 \text { vs. } H_{1}: \sigma^{2} \neq 1$$

  where $\Theta_{0}=\{(\mu, 1): \mu \in \mathbb{R}\}$ is the parameter space constrained by $H_{0}$.

  Prove carefully that

  $$\Lambda_{n}\left(\Theta, \Theta_{0}\right) \rightarrow^{d} \chi_{1}^{2} \quad \text { as } n \rightarrow \infty$$

  where $\chi_{1}^{2}$ is a Chi-Square distribution with one degree of freedom.

  comment

Probability and Measure

• Paper 2, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2020

  Let $X$ be a set. Recall that a Boolean algebra $\mathcal{B}$ of subsets of $X$ is a family of subsets containing the empty set, which is stable under finite union and under taking complements. As usual, let $\sigma(\mathcal{B})$ be the $\sigma$-algebra generated by $\mathcal{B}$.

  (a) State the definitions of a $\sigma$-algebra, that of a measure on a measurable space, as well as the definition of a probability measure.

  (b) State Carathéodory's extension theorem.

  (c) Let $(X, \mathcal{F}, \mu)$ be a probability measure space. Let $\mathcal{B} \subset \mathcal{F}$ be a Boolean algebra of subsets of $X$. Let $\mathcal{C}$ be the family of all $A \in \mathcal{F}$ with the property that for every $\epsilon>0$, there is $B \in \mathcal{B}$ such that

  $$\mu(A \triangle B)<\epsilon,$$

  where $A \triangle B$ denotes the symmetric difference of $A$ and $B$, i.e., $A \triangle B=(A \cup B) \backslash(A \cap B)$.

  (i) Show that $\sigma(\mathcal{B})$ is contained in $\mathcal{C}$. Show by example that this may fail if $\mu(X)=+\infty$.

  (ii) Now assume that $(X, \mathcal{F}, \mu)=\left([0,1], \mathcal{L}_{[0,1]}, m\right)$, where $\mathcal{L}_{[0,1]}$ is the $\sigma$-algebra of Lebesgue measurable subsets of $[0,1]$ and $m$ is the Lebesgue measure. Let $\mathcal{B}$ be the family of all finite unions of sub-intervals. Is it true that $\mathcal{C}$ is equal to $\mathcal{L}_{[0,1]}$ in this case? Justify your answer.

  comment

Quantum Information and Computation

• Paper 2, Section I, 10C

  Quantum Information and Computation | Part II, 2020

  Consider the set of states

  $$\left|\beta_{z x}\right\rangle:=\frac{1}{\sqrt{2}}\left[|0 x\rangle+(-1)^{z}|1 \bar{x}\rangle\right],$$

  where $x, z \in\{0,1\}$ and $\bar{x}=x \oplus 1$ (addition modulo 2 ).

  (i) Show that

  $$(H \otimes \mathbb{I}) \circ \mathrm{CX}\left|\beta_{z x}\right\rangle=|z x\rangle \quad \forall z, x \in\{0,1\},$$

  where $H$ denotes the Hadamard gate and CX denotes the controlled- $X$ gate.

  (ii) Show that for any $z, x \in\{0,1\}$,

  $$\tag{*} \left(Z^{z} X^{x} \otimes \mathbb{I}\right)\left|\beta_{00}\right\rangle=\left|\beta_{z x}\right\rangle .$$

  [Hint: For any unitary operator $U$, we have $(U \otimes \mathbb{I})\left|\beta_{00}\right\rangle=\left(\mathbb{I} \otimes U^{T}\right)\left|\beta_{00}\right\rangle$, where $U^{T}$ denotes the transpose of $U$ with respect to the computational basis.]

  (iii) Suppose Alice and Bob initially share the state $\left|\beta_{00}\right\rangle$. Show using (*) how Alice can communicate two classical bits to Bob by sending him only a single qubit.

  comment

• Paper 2, Section II, 15C

  Quantum Information and Computation | Part II, 2020

  (a) Show how the $n$-qubit state

  $$\left|\psi_{n}\right\rangle:=\frac{1}{\sqrt{2^{n}}} \sum_{x \in B_{n}}|x\rangle$$

  can be generated from a computational basis state of $\mathbb{C}^{n}$ by the action of Hadamard gates.

  (b) Prove that $C Z=(I \otimes H) C N O T_{12}(I \otimes H)$, where $C Z$ denotes the controlled- $Z$ gate. Justify (without any explicit calculations) the following identity:

  $$C N O T_{12}=(I \otimes H) C Z(I \otimes H)$$

  (c) Consider the following two-qubit circuit:

  

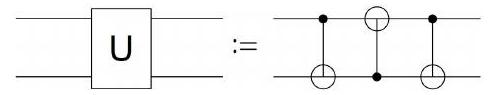
  What is its action on an arbitrary 2-qubit state $|\psi\rangle \otimes|\phi\rangle ?$ In particular, for two given states $|\psi\rangle$ and $|\phi\rangle$, find the states $|\alpha\rangle$ and $|\beta\rangle$ such that

  $$U(|\psi\rangle \otimes|\phi\rangle)=|\alpha\rangle \otimes|\beta\rangle .$$

  (d) Consider the following quantum circuit diagram

  

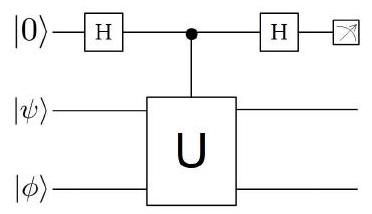
  where the measurement is relative to the computational basis and $U$ is the quantum gate from part (c). Note that the second gate in the circuit performs the following controlled operation:

  $$|0\rangle|\psi\rangle|\phi\rangle \mapsto|0\rangle|\psi\rangle|\phi\rangle ;|1\rangle|\psi\rangle|\phi\rangle \mapsto|1\rangle U(|\psi\rangle|\phi\rangle) .$$

  (i) Give expressions for the joint state of the three qubits after the action of the first Hadamard gate; after the action of the quantum gate $U$; and after the action of the second Hadamard gate.

  (ii) Compute the probabilities $p_{0}$ and $p_{1}$ of getting outcome 0 and 1 , respectively, in the measurement.

  (iii) How can the above circuit be used to determine (with high probability) whether the two states $|\psi\rangle$ and $|\phi\rangle$ are identical or not? [Assume that you are given arbitrarily many copies of the three input states and that the quantum circuit can be used arbitrarily many times.]

  comment

Representation Theory

• Paper 2, Section II, F

  Representation Theory | Part II, 2020

  Let $G$ be the unique non-abelian group of order 21 up to isomorphism. Compute the character table of $G$.

  [You may find it helpful to think of $G$ as the group of $2 \times 2$ matrices of the form $\left(\begin{array}{cc}a & b \\ 0 & a^{-1}\end{array}\right)$ with $a, b \in \mathbb{F}_{7}$ and $a^{3}=1$. You may use any standard results from the course provided you state them clearly.]

  comment

Riemann Surfaces

• Paper 2, Section II, 23F

  Riemann Surfaces | Part II, 2020

  Let $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ be a rational function. What does it mean for $p \in \mathbb{C}_{\infty}$ to be a ramification point? What does it mean for $p \in \mathbb{C}_{\infty}$ to be a branch point?

  Let $B$ be the set of branch points of $f$, and let $R$ be the set of ramification points. Show that

  $$f: \mathbb{C}_{\infty} \backslash R \rightarrow \mathbb{C}_{\infty} \backslash B$$

  is a regular covering map.

  State the monodromy theorem. For $w \in \mathbb{C}_{\infty} \backslash B$, explain how a closed curve based at $w$ defines a permutation of $f^{-1}(w)$.

  For the rational function

  $$f(z)=\frac{z(2-z)}{(1-z)^{4}}$$

  identify the group of all such permutations.

  comment

Statistical Modelling

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2020

  The data frame WCG contains data from a study started in 1960 about heart disease. The study used 3154 adult men, all free of heart disease at the start, and eight and a half years later it recorded into variable chd whether they suffered from heart disease (1 if the respective man did and 0 otherwise) along with their height and average number of cigarettes smoked per day. Consider the $\mathrm{R}$ code below and its abbreviated output.

  

  (a) Write down the model fitted by the code above.

  (b) Interpret the effect on heart disease of a man smoking an average of two packs of cigarettes per day if each pack contains 20 cigarettes.

  (c) Give an alternative latent logistic-variable representation of the model. [Hint: if $F$ is the cumulative distribution function of a logistic random variable, its inverse function is the logit function.]

  comment

Statistical Physics

• Paper 2, Section II, A

  Statistical Physics | Part II, 2020

  Using the Gibbs free energy $G(T, P)=E-T S+P V$, derive the Maxwell relation

  $$\left.\frac{\partial S}{\partial P}\right|_{T}=-\left.\frac{\partial V}{\partial T}\right|_{P}$$

  Define the notions of heat capacity at constant volume, $C_{V}$, and heat capacity at constant pressure, $C_{P}$. Show that

  $$C_{P}-C_{V}=\left.\left.T \frac{\partial V}{\partial T}\right|_{P} \frac{\partial P}{\partial T}\right|_{V}$$

  Derive the Clausius-Clapeyron relation for $\frac{d P}{d T}$ along the first-order phase transition curve between a liquid and a gas. Find the simplified form of this relation, assuming the gas has much larger volume than the liquid and that the gas is ideal. Assuming further that the latent heat is a constant, determine the form of $P$ as a function of $T$ along the phase transition curve. [You may assume there is no discontinuity in the Gibbs free energy across the phase transition curve.]

  comment

Stochastic Financial Models

• Paper 2, Section II, 29K

  Stochastic Financial Models | Part II, 2020

  Let $\left(S_{n}^{0}, S_{n}\right)_{0 \leqslant n \leqslant T}$ be a discrete-time asset price model in $\mathbb{R}^{d+1}$ with numéraire.

  (i) What is meant by an arbitrage for such a model?

  (ii) What does it mean to say that the model is complete?

  Consider now the case where $d=1$ and where

  $$S_{n}^{0}=(1+r)^{n}, \quad S_{n}=S_{0} \prod_{k=1}^{n} Z_{k}$$

  for some $r>0$ and some independent positive random variables $Z_{1}, \ldots, Z_{T}$ with $\log Z_{n} \sim N\left(\mu, \sigma^{2}\right)$ for all $n$.

  (iii) Find an equivalent probability measure $\mathbb{P}^{*}$ such that the discounted asset price $\left(S_{n} / S_{n}^{0}\right)_{0 \leqslant n \leqslant T}$ is a martingale.

  (iv) Does this model have an arbitrage? Justify your answer.

  (v) By considering the contingent claim $\left(S_{1}\right)^{2}$ or otherwise, show that this model is not complete.

  comment

Topics in Analysis

• Paper 2, Section I, $2 \mathrm{H}$

  Topics in Analysis | Part II, 2020

  Show that every Legendre polynomial $p_{n}$ has $n$ distinct roots in $[-1,1]$, where $n$ is the degree of $p_{n}$.

  Let $x_{1}, \ldots, x_{n}$ be distinct numbers in $[-1,1]$. Show that there are unique real numbers $A_{1}, \ldots, A_{n}$ such that the formula

  $$\int_{-1}^{1} P(t) d t=\sum_{i=1}^{n} A_{i} P\left(x_{i}\right)$$

  holds for every polynomial $P$ of degree less than $n$.

  Now suppose that the above formula in fact holds for every polynomial $P$ of degree less than $2 n$. Show that then $x_{1}, \ldots, x_{n}$ are the roots of $p_{n}$. Show also that $\sum_{i=1}^{n} A_{i}=2$ and that all $A_{i}$ are positive.

  comment

• Paper 2, Section II, H

  Topics in Analysis | Part II, 2020

  Let $T$ be a (closed) triangle in $\mathbb{R}^{2}$ with edges $I, J, K$. Let $A, B, C$, be closed subsets of $T$, such that $I \subset A, J \subset B, K \subset C$ and $T=A \cup B \cup C$. Prove that $A \cap B \cap C$ is non-empty.

  Deduce that there is no continuous map $f: D \rightarrow \partial D$ such that $f(p)=p$ for all $p \in \partial D$, where $D=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2} \leqslant 1\right\}$ is the closed unit disc and $\partial D=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}$ is its boundary.

  Let now $\alpha, \beta, \gamma \subset \partial D$ be three closed arcs, each arc making an angle of $2 \pi / 3$ (in radians) in $\partial D$ and $\alpha \cup \beta \cup \gamma=\partial D$. Let $P, Q$ and $R$ be open subsets of $D$, such that $\alpha \subset P$, $\beta \subset Q$ and $\gamma \subset R$. Suppose that $P \cup Q \cup R=D$. Show that $P \cap Q \cap R$ is non-empty. [You may assume that for each closed bounded subset $K \subset \mathbb{R}^{2}, d(x, K)=\min \{\|x-y\|: y \in K\}$ defines a continuous function on $\mathbb{R}^{2}$.]

  comment

Waves

• Paper 2, Section II, 39B

  Waves | Part II, 2020

  Small displacements $\mathbf{u}(\mathbf{x}, t)$ in a homogeneous elastic medium are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \wedge(\boldsymbol{\nabla} \wedge \mathbf{u})$$

  where $\rho$ is the density, and $\lambda$ and $\mu$ are the Lamé constants.

  (a) Show that the equation supports two types of harmonic plane-wave solutions, $\mathbf{u}=\mathbf{A} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)]$, with distinct wavespeeds, $c_{P}$ and $c_{S}$, and distinct polarizations. Write down the direction of the displacement vector A for a $P$-wave, an $S V$-wave and an $S H$-wave, in each case for the wavevector $(k, 0, m)$.

  (b) Given $k$ and $c$, with $c>c_{P}\left(>c_{S}\right)$, explain how to construct a superposition of $P$-waves with wavenumbers $\left(k, 0, m_{P}\right)$ and $\left(k, 0,-m_{P}\right)$, such that

  $$\mathbf{u}(x, z, t)=e^{i k(x-c t)}\left(f_{1}(z), 0, i f_{3}(z)\right)$$

  where $f_{1}(z)$ is an even function, and $f_{1}$ and $f_{3}$ are both real functions, to be determined. Similarly, find a superposition of $S V$-waves with $\mathbf{u}$ again in the form $(*)$.

  (c) An elastic waveguide consists of an elastic medium in $-H<z<H$ with rigid boundaries at $z=\pm H$. Using your answers to part (b), show that the waveguide supports propagating eigenmodes that are a mixture of $P$ - and $S V$-waves, and have dispersion relation $c(k)$ given by

  $$a \tan (a k H)=-\frac{\tan (b k H)}{b}, \quad \text { where } \quad a=\left(\frac{c^{2}}{c_{P}^{2}}-1\right)^{1 / 2} \quad \text { and } \quad b=\left(\frac{c^{2}}{c_{S}^{2}}-1\right)^{1 / 2}$$

  Sketch the two sides of the dispersion relationship as functions of $c$. Explain briefly why there are infinitely many solutions.

  comment