Part II, 2020, Paper 1

Algebraic Geometry

• Paper 1, Section II, F

  Algebraic Geometry | Part II, 2020

  Let $k$ be an algebraically closed field of characteristic zero. Prove that an affine variety $V \subset \mathbb{A}_{k}^{n}$ is irreducible if and only if the associated ideal $I(V)$ of polynomials that vanish on $V$ is prime.

  Prove that the variety $\mathbb{V}\left(y^{2}-x^{3}\right) \subset \mathbb{A}_{k}^{2}$ is irreducible.

  State what it means for an affine variety over $k$ to be smooth and determine whether or not $\mathbb{V}\left(y^{2}-x^{3}\right)$ is smooth.

  comment

Algebraic Topology

• Paper 1, Section II, $21 \mathbf{F}$

  Algebraic Topology | Part II, 2020

  Let $p: \mathbb{R}^{2} \rightarrow S^{1} \times S^{1}=: X$ be the map given by

  $$p\left(r_{1}, r_{2}\right)=\left(e^{2 \pi i r_{1}}, e^{2 \pi i r_{2}}\right)$$

  where $S^{1}$ is identified with the unit circle in $\mathbb{C}$. [You may take as given that $p$ is a covering map.]

  (a) Using the covering map $p$, show that $\pi_{1}\left(X, x_{0}\right)$ is isomorphic to $\mathbb{Z}^{2}$ as a group, where $x_{0}=(1,1) \in X$.

  (b) Let $\mathrm{GL}_{2}(\mathbb{Z})$ denote the group of $2 \times 2$ matrices $A$ with integer entries such that $\operatorname{det} A=\pm 1$. If $A \in \mathrm{GL}_{2}(\mathbb{Z})$, we obtain a linear transformation $A: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$. Show that this linear transformation induces a homeomorphism $f_{A}: X \rightarrow X$ with $f_{A}\left(x_{0}\right)=x_{0}$ and such that $f_{A *}: \pi_{1}\left(X, x_{0}\right) \rightarrow \pi_{1}\left(X, x_{0}\right)$ agrees with $A$ as a map $\mathbb{Z}^{2} \rightarrow \mathbb{Z}^{2}$.

  (c) Let $p_{i}: \widehat{X}_{i} \rightarrow X$ for $i=1,2$ be connected covering maps of degree 2 . Show that there exist homeomorphisms $\phi: \widehat{X}_{1} \rightarrow \widehat{X}_{2}$ and $\psi: X \rightarrow X$ so that the diagram

  

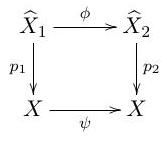
  is commutative.

  comment

Analysis of Functions

• Paper 1, Section II, I

  Analysis of Functions | Part II, 2020

  Let $\mathbb{R}^{n}$ be equipped with the $\sigma$-algebra of Lebesgue measurable sets, and Lebesgue measure.

  (a) Given $f \in L^{\infty}\left(\mathbb{R}^{n}\right), g \in L^{1}\left(\mathbb{R}^{n}\right)$, define the convolution $f \star g$, and show that it is a bounded, continuous function. [You may use without proof continuity of translation on $L^{p}\left(\mathbb{R}^{n}\right)$ for $\left.1 \leqslant p<\infty .\right]$

  Suppose $A \subset \mathbb{R}^{n}$ is a measurable set with $0<|A|<\infty$ where $|A|$ denotes the Lebesgue measure of $A$. By considering the convolution of $f(x)=\mathbb{1}_{A}(x)$ and $g(x)=\mathbb{1}_{A}(-x)$, or otherwise, show that the set $A-A=\{x-y: x, y \in A\}$ contains an open neighbourhood of 0 . Does this still hold if $|A|=\infty$ ?

  (b) Suppose that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is a measurable function satisfying

  $$f(x+y)=f(x)+f(y), \quad \text { for all } x, y \in \mathbb{R}^{n}$$

  Let $B_{r}=\left\{y \in \mathbb{R}^{m}:|y|<r\right\}$. Show that for any $\epsilon>0$ :

  (i) $f^{-1}\left(B_{\epsilon}\right)-f^{-1}\left(B_{\epsilon}\right) \subset f^{-1}\left(B_{2 \epsilon}\right)$,

  (ii) $f^{-1}\left(B_{k \epsilon}\right)=k f^{-1}\left(B_{\epsilon}\right)$ for all $k \in \mathbb{N}$, where for $\lambda>0$ and $A \subset \mathbb{R}^{n}, \lambda A$ denotes the set $\{\lambda x: x \in A\}$.

  Show that $f$ is continuous at 0 and hence deduce that $f$ is continuous everywhere.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, C

  Applications of Quantum Mechanics | Part II, 2020

  Consider the quantum mechanical scattering of a particle of mass $m$ in one dimension off a parity-symmetric potential, $V(x)=V(-x)$. State the constraints imposed by parity, unitarity and their combination on the components of the $S$-matrix in the parity basis,

  $$S=\left(\begin{array}{cc} S_{++} & S_{+-} \\ S_{-+} & S_{--} \end{array}\right)$$

  For the specific potential

  $$V=\hbar^{2} \frac{U_{0}}{2 m}\left[\delta_{D}(x+a)+\delta_{D}(x-a)\right]$$

  show that

  $$S_{--}=e^{-i 2 k a}\left[\frac{\left(2 k-i U_{0}\right) e^{i k a}+i U_{0} e^{-i k a}}{\left(2 k+i U_{0}\right) e^{-i k a}-i U_{0} e^{i k a}}\right]$$

  For $U_{0}<0$, derive the condition for the existence of an odd-parity bound state. For $U_{0}>0$ and to leading order in $U_{0} a \gg 1$, show that an odd-parity resonance exists and discuss how it evolves in time.

  comment

Applied Probability

• Paper 1, Section II, 28K

  Applied Probability | Part II, 2020

  (a) What is meant by a birth process $N=(N(t): t \geqslant 0)$ with strictly positive rates $\lambda_{0}, \lambda_{1}, \ldots ?$ Explain what is meant by saying that $N$ is non-explosive.

  (b) Show that $N$ is non-explosive if and only if

  $$\sum_{n=0}^{\infty} \frac{1}{\lambda_{n}}=\infty$$

  (c) Suppose $N(0)=0$, and $\lambda_{n}=\alpha n+\beta$ where $\alpha, \beta>0$. Show that

  $$\mathbb{E}(N(t))=\frac{\beta}{\alpha}\left(e^{\alpha t}-1\right) .$$

  comment

Automata and Formal Languages

• Paper 1, Section I, $4 \mathbf{F}$

  Automata and Formal Languages | Part II, 2020

  Define an alphabet $\Sigma$, a word over $\Sigma$ and a language over $\Sigma$.

  What is a regular expression $R$ and how does this give rise to a language $\mathcal{L}(R) ?$

  Given any alphabet $\Sigma$, show that there exist languages $L$ over $\Sigma$ which are not equal to $\mathcal{L}(R)$ for any regular expression $R$. [You are not required to exhibit a specific $L$.]

  comment

• Paper 1, Section II, F

  Automata and Formal Languages | Part II, 2020

  (a) Define a register machine, a sequence of instructions for a register machine and a partial computable function. How do we encode a register machine?

  (b) What is a partial recursive function? Show that a partial computable function is partial recursive. [You may assume that for a given machine with a given number of inputs, the function outputting its state in terms of the inputs and the time $t$ is recursive.]

  (c) (i) Let $g: \mathbb{N} \rightarrow \mathbb{N}$ be the partial function defined as follows: if $n$ codes a register machine and the ensuing partial function $f_{n, 1}$ is defined at $n$, set $g(n)=f_{n, 1}(n)+1$. Otherwise set $g(n)=0$. Is $g$ a partial computable function?

  (ii) Let $h: \mathbb{N} \rightarrow \mathbb{N}$ be the partial function defined as follows: if $n$ codes a register machine and the ensuing partial function $f_{n, 1}$ is defined at $n$, set $h(n)=f_{n, 1}(n)+1$. Otherwise, set $h(n)=0$ if $n$ is odd and let $h(n)$ be undefined if $n$ is even. Is $h$ a partial computable function?

  comment

Classical Dynamics

• Paper 1, Section I, B

  Classical Dynamics | Part II, 2020

  A linear molecule is modelled as four equal masses connected by three equal springs. Using the Cartesian coordinates $x_{1}, x_{2}, x_{3}, x_{4}$ of the centres of the four masses, and neglecting any forces other than those due to the springs, write down the Lagrangian of the system describing longitudinal motions of the molecule.

  Rewrite and simplify the Lagrangian in terms of the generalized coordinates

  $$q_{1}=\frac{x_{1}+x_{4}}{2}, \quad q_{2}=\frac{x_{2}+x_{3}}{2}, \quad q_{3}=\frac{x_{1}-x_{4}}{2}, \quad q_{4}=\frac{x_{2}-x_{3}}{2}$$

  Deduce Lagrange's equations for $q_{1}, q_{2}, q_{3}, q_{4}$. Hence find the normal modes of the system and their angular frequencies, treating separately the symmetric and antisymmetric modes of oscillation.

  comment

Coding and Cryptography

• Paper 1, Section I, I

  Coding and Cryptography | Part II, 2020

  (a) Briefly describe the methods of Shannon-Fano and of Huffman for the construction of prefix-free binary codes.

  (b) In this part you are given that $-\log _{2}(1 / 10) \approx 3.32,-\log _{2}(2 / 10) \approx 2.32$, $-\log _{2}(3 / 10) \approx 1.74$ and $-\log _{2}(4 / 10) \approx 1.32$.

  Let $\mathcal{A}=\{1,2,3,4\}$. For $k \in \mathcal{A}$, suppose that the probability of choosing $k$ is $k / 10$.

  (i) Find a Shannon-Fano code for this system and the expected word length.

  (ii) Find a Huffman code for this system and the expected word length.

  (iii) Verify that Shannon's noiseless coding theorem is satisfied in each case.

  comment

• Paper 1, Section II, I

  Coding and Cryptography | Part II, 2020

  (a) What does it mean to say that a binary code has length $n$, size $M$ and minimum distance d?

  Let $A(n, d)$ be the largest value of $M$ for which there exists a binary $[n, M, d]$-code.

  (i) Show that $A(n, 1)=2^{n}$.

  (ii) Suppose that $n, d>1$. Show that if a binary $[n, M, d]$-code exists, then a binary $[n-1, M, d-1]$-code exists. Deduce that $A(n, d) \leqslant A(n-1, d-1)$.

  (iii) Suppose that $n, d \geqslant 1$. Show that $A(n, d) \leqslant 2^{n-d+1}$.

  (b) (i) For integers $M$ and $N$ with $0 \leqslant N \leqslant M$, show that

  $$N(M-N) \leqslant\left\{\begin{array}{cl} M^{2} / 4, & \text { if } M \text { is even }, \\ \left(M^{2}-1\right) / 4, & \text { if } M \text { is odd } \end{array}\right.$$

  For the remainder of this question, suppose that $C$ is a binary $[n, M, d]$-code. For codewords $x=\left(x_{1} \ldots x_{n}\right), y=\left(y_{1} \ldots y_{n}\right) \in C$ of length $n$, we define $x+y$ to be the word $\left(\left(x_{1}+y_{1}\right) \ldots\left(x_{n}+y_{n}\right)\right)$ with addition modulo $2 .$

  (ii) Explain why the Hamming distance $d(x, y)$ is the number of 1 s in $x+y$.

  (iii) Now we construct an $\left(\begin{array}{c}M \\ 2\end{array}\right) \times n$ array $A$ whose rows are all the words $x+y$ for pairs of distinct codewords $x, y$. Show that the number of $1 \mathrm{~s}$ in $A$ is at most

  $$\begin{cases}n M^{2} / 4, & \text { if } M \text { is even } \\ n\left(M^{2}-1\right) / 4, & \text { if } M \text { is odd }\end{cases}$$

  Show also that the number of $1 \mathrm{~s}$ in $A$ is at least $d\left(\begin{array}{c}M \\ 2\end{array}\right)$.

  (iv) Using the inequalities derived in part(b) (iii), deduce that if $d$ is even and $n<2 d$ then

  $$A(n, d) \leqslant 2\left\lfloor\frac{d}{2 d-n}\right\rfloor$$

  comment

Cosmology

• Paper 1, Section I, D

  Cosmology | Part II, 2020

  The Friedmann equation is

  $$H^{2}=\frac{8 \pi G}{3 c^{2}}\left(\rho-\frac{k c^{2}}{R^{2} a^{2}}\right)$$

  Briefly explain the meaning of $H, \rho, k$ and $R$.

  Derive the Raychaudhuri equation,

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3 c^{2}}(\rho+3 P),$$

  where $P$ is the pressure, stating clearly any results that are required.

  Assume that the strong energy condition $\rho+3 P \geqslant 0$ holds. Show that there was necessarily a Big Bang singularity at time $t_{B B}$ such that

  $$t_{0}-t_{B B} \leqslant H_{0}^{-1}$$

  where $H_{0}=H\left(t_{0}\right)$ and $t_{0}$ is the time today.

  comment

• Paper 1, Section II, D

  Cosmology | Part II, 2020

  A fluid with pressure $P$ sits in a volume $V$. The change in energy due to a change in volume is given by $d E=-P d V$. Use this in a cosmological context to derive the continuity equation,

  $$\dot{\rho}=-3 H(\rho+P),$$

  with $\rho$ the energy density, $H=\dot{a} / a$ the Hubble parameter, and $a$ the scale factor.

  In a flat universe, the Friedmann equation is given by

  $$H^{2}=\frac{8 \pi G}{3 c^{2}} \rho .$$

  Given a universe dominated by a fluid with equation of state $P=w \rho$, where $w$ is a constant, determine how the scale factor $a(t)$ evolves.

  Define conformal time $\tau$. Assume that the early universe consists of two fluids: radiation with $w=1 / 3$ and a network of cosmic strings with $w=-1 / 3$. Show that the Friedmann equation can be written as

  $$\left(\frac{d a}{d \tau}\right)^{2}=B \rho_{\mathrm{eq}}\left(a^{2}+a_{\mathrm{eq}}^{2}\right)$$

  where $\rho_{\mathrm{eq}}$ is the energy density in radiation, and $a_{\mathrm{eq}}$ is the scale factor, both evaluated at radiation-string equality. Here, $B$ is a constant that you should determine. Find the solution $a(\tau)$.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2020

  (a) Let $X \subset \mathbb{R}^{N}$ be a manifold. Give the definition of the tangent space $T_{p} X$ of $X$ at a point $p \in X$.

  (b) Show that $X:=\left\{-x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=-1\right\} \cap\left\{x_{0}>0\right\}$ defines a submanifold of $\mathbb{R}^{4}$ and identify explicitly its tangent space $T_{\mathbf{x}} X$ for any $\mathbf{x} \in X$.

  (c) Consider the matrix group $O(1,3) \subset \mathbb{R}^{4^{2}}$ consisting of all $4 \times 4$ matrices $A$ satisfying

  $$A^{t} M A=M$$

  where $M$ is the diagonal $4 \times 4$ matrix $M=\operatorname{diag}(-1,1,1,1)$.

  (i) Show that $O(1,3)$ forms a group under matrix multiplication, i.e. it is closed under multiplication and every element in $O(1,3)$ has an inverse in $O(1,3)$.

  (ii) Show that $O(1,3)$ defines a 6-dimensional manifold. Identify the tangent space $T_{A} O(1,3)$ for any $A \in O(1,3)$ as a set $\{A Y\}_{Y \in \mathfrak{S}}$ where $Y$ ranges over a linear subspace $\mathfrak{S} \subset \mathbb{R}^{4^{2}}$ which you should identify explicitly.

  (iii) Let $X$ be as defined in (b) above. Show that $O^{+}(1,3) \subset O(1,3)$ defined as the set of all $A \in O(1,3)$ such that $A \mathbf{x} \in X$ for all $\mathbf{x} \in X$ is both a subgroup and a submanifold of full dimension.

  [You may use without proof standard theorems from the course concerning regular values and transversality.]

  comment

Dynamical Systems

• Paper 1, Section II, 32E

  Dynamical Systems | Part II, 2020

  (i) For the dynamical system

  $$\dot{x}=-x\left(x^{2}-2 \mu\right)\left(x^{2}-\mu+a\right),$$

  sketch the bifurcation diagram in the $(\mu, x)$ plane for the three cases $a<0, a=0$ and $a>0$. Describe the bifurcation points that occur in each case.

  (ii) For the case when $a<0$ only, confirm the types of bifurcation by finding the system to leading order near each of the bifurcations.

  (iii) Explore the structural stability of these bifurcations by adding a small positive constant $\epsilon$ to the right-hand side of $(\uparrow)$ and by sketching the bifurcation diagrams, for the three cases $a<0, a=0$ and $a>0$. Which of the original bifurcations are structurally stable?

  comment

Electrodynamics

• Paper 1, Section II, 37D

  Electrodynamics | Part II, 2020

  A relativistic particle of rest mass $m$ and electric charge $q$ follows a worldline $x^{\mu}(\lambda)$ in Minkowski spacetime where $\lambda=\lambda(\tau)$ is an arbitrary parameter which increases monotonically with the proper time $\tau$. We consider the motion of the particle in a background electromagnetic field with four-vector potential $A^{\mu}(x)$ between initial and final values of the proper time denoted $\tau_{i}$ and $\tau_{f}$ respectively.

  (i) Write down an action for the particle's motion. Explain what is meant by a gauge transformation of the electromagnetic field. How does the action change under a gauge transformation?

  (ii) Derive an equation of motion for the particle by considering the variation of the action with respect to the worldline $x^{\mu}(\lambda)$. Setting $\lambda=\tau$ show that your equation of motion reduces to the Lorentz force law,

  $$m \frac{d u^{\mu}}{d \tau}=q F^{\mu \nu} u_{\nu}$$

  where $u^{\mu}=d x^{\mu} / d \tau$ is the particle's four-velocity and $F^{\mu \nu}=\partial^{\mu} A^{\nu}-\partial^{\nu} A^{\mu}$ is the Maxwell field-strength tensor.

  (iii) Working in an inertial frame with spacetime coordinates $x^{\mu}=(c t, x, y, z)$, consider the case of a constant, homogeneous magnetic field of magnitude $B$, pointing in the $z$-direction, and vanishing electric field. In a gauge where $A^{\mu}=(0,0, B x, 0)$, show that the equation of motion $(*)$ is solved by circular motion in the $x-y$ plane with proper angular frequency $\omega=q B / m$.

  (iv) Let $v$ denote the speed of the particle in this inertial frame with Lorentz factor $\gamma(v)=1 / \sqrt{1-v^{2} / c^{2}}$. Find the radius $R=R(v)$ of the circle as a function of $v$. Setting $\tau_{f}=\tau_{i}+2 \pi / \omega$, evaluate the action $S=S(v)$ for a single period of the particle's motion.

  comment

Fluid Dynamics II

• Paper 1, Section II, 39B

  Fluid Dynamics II | Part II, 2020

  A viscous fluid is confined between an inner, impermeable cylinder of radius $a$ with centre at $(x, y)=(0, a)$ and another outer, impermeable cylinder of radius $2 a$ with centre at $(0,2 a)$ (so they touch at the origin and both have their axes in the $z$ direction). The inner cylinder rotates about its axis with angular velocity $\Omega$ and the outer cylinder rotates about its axis with angular velocity $-\Omega / 4$. The fluid motion is two-dimensional and slow enough that the Stokes approximation is appropriate.

  (i) Show that the boundary of the inner cylinder is described by the relationship

  $$r=2 a \sin \theta,$$

  where $(r, \theta)$ are the usual polar coordinates centred on $(x, y)=(0,0)$. Show also that on this cylinder the boundary condition on the tangential velocity can be written as

  $$u_{r} \cos \theta+u_{\theta} \sin \theta=a \Omega,$$

  where $u_{r}$ and $u_{\theta}$ are the components of the velocity in the $r$ and $\theta$ directions respectively. Explain why the boundary condition $\psi=0$ (where $\psi$ is the streamfunction such that $u_{r}=\frac{1}{r} \frac{\partial \psi}{\partial \theta}$ and $\left.u_{\theta}=-\frac{\partial \psi}{\partial r}\right)$ can be imposed.

  (ii) Write down the boundary conditions to be satisfied on the outer cylinder $r=4 a \sin \theta$, explaining carefully why $\psi=0$ can also be imposed on this cylinder as well.

  (iii) It is given that the streamfunction is of the form

  $$\psi=A \sin ^{2} \theta+B r^{2}+C r \sin \theta+D \sin ^{3} \theta / r$$

  where $A, B, C$ and $D$ are constants, which satisfies $\nabla^{4} \psi=0$. Using the fact that $B=0$ due to the symmetry of the problem, show that the streamfunction is

  $$\psi=\frac{\alpha \sin \theta}{r}(r-2 a \sin \theta)(r-4 a \sin \theta)$$

  where the constant $\alpha$ is to be found.

  (iv) Sketch the streamline pattern between the cylinders and determine the $(x, y)$ coordinates of the stagnation point in the flow.

  comment

Further Complex Methods

• Paper 1, Section I, 7 E

  Further Complex Methods | Part II, 2020

  The function $I(z)$, defined by

  $$I(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t$$

  is analytic for $\operatorname{Re} z>0$.

  (i) Show that $I(z+1)=z I(z)$.

  (ii) Use part (i) to construct an analytic continuation of $I(z)$ into Re $z \leqslant 0$, except at isolated singular points, which you need to identify.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2020

  Use the change of variable $z=\sin ^{2} x$, to rewrite the equation

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=0$$

  where $k$ is a real non-zero number, as the hypergeometric equation

  $$\frac{d^{2} w}{d z^{2}}+\left(\frac{C}{z}+\frac{1+A+B-C}{z-1}\right) \frac{d w}{d z}+\frac{A B}{z(z-1)} w=0$$

  where $y(x)=w(z)$, and $A, B$ and $C$ should be determined explicitly.

  (i) Show that ( $\$)$ is a Papperitz equation, with 0,1 and $\infty$ as its regular singular points. Hence, write the corresponding Papperitz symbol,

  $$P\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & A \\ 1-C & C-A-B & B \end{array}\right\}$$

  in terms of $k$.

  (ii) By solving ( $\dagger$ ) directly or otherwise, find the hypergeometric function $F(A, B ; C ; z)$ that is the solution to $(\ddagger)$ and is analytic at $z=0$ corresponding to the exponent 0 at $z=0$, and satisfies $F(A, B ; C ; 0)=1$; moreover, write it in terms of $k$ and

  (iii) By performing a suitable exponential shifting find the second solution, independent of $F(A, B ; C ; z)$, which corresponds to the exponent $1-C$, and hence write $F\left(\frac{1+k}{2}, \frac{1-k}{2} ; \frac{3}{2} ; z\right)$ in terms of $k$ and $x$.

  comment

Galois Theory

• Paper 1, Section II, 18G

  Galois Theory | Part II, 2020

  (a) State and prove the tower law.

  (b) Let $K$ be a field and let $f(x) \in K[x]$.

  (i) Define what it means for an extension $L / K$ to be a splitting field for $f$.

  (ii) Suppose $f$ is irreducible in $K[x]$, and char $K=0$. Let $M / K$ be an extension of fields. Show that the roots of $f$ in $M$ are distinct.

  (iii) Let $h(x)=x^{q^{n}}-x \in K[x]$, where $K=F_{q}$ is the finite field with $q$ elements. Let $L$ be a splitting field for $h$. Show that the roots of $h$ in $L$ are distinct. Show that $[L: K]=n$. Show that if $f(x) \in K[x]$ is irreducible, and deg $f=n$, then $f$ divides $x^{q^{n}}-x$.

  (iv) For each prime $p$, give an example of a field $K$, and a polynomial $f(x) \in K[x]$ of degree $p$, so that $f$ has at most one root in any extension $L$ of $K$, with multiplicity $p$.

  comment

General Relativity

• Paper 1, Section II, 38D

  General Relativity | Part II, 2020

  Let $(\mathcal{M}, \boldsymbol{g})$ be a four-dimensional manifold with metric $g_{\alpha \beta}$ of Lorentzian signature.

  The Riemann tensor $\boldsymbol{R}$ is defined through its action on three vector fields $\boldsymbol{X}, \boldsymbol{V}, \boldsymbol{W}$ by

  $$\boldsymbol{R}(\boldsymbol{X}, \boldsymbol{V}) \boldsymbol{W}=\nabla_{\boldsymbol{X}} \nabla_{\boldsymbol{V}} \boldsymbol{W}-\nabla_{\boldsymbol{V}} \nabla_{\boldsymbol{X}} \boldsymbol{W}-\nabla_{[\boldsymbol{X}, \boldsymbol{V}]} \boldsymbol{W}$$

  and the Ricci identity is given by

  $$\nabla_{\alpha} \nabla_{\beta} V^{\gamma}-\nabla_{\beta} \nabla_{\alpha} V^{\gamma}=R_{\rho \alpha \beta}^{\gamma} V^{\rho} .$$

  (i) Show that for two arbitrary vector fields $\boldsymbol{V}, \boldsymbol{W}$, the commutator obeys

  $$[\boldsymbol{V}, \boldsymbol{W}]^{\alpha}=V^{\mu} \nabla_{\mu} W^{\alpha}-W^{\mu} \nabla_{\mu} V^{\alpha}$$

  (ii) Let $\gamma: I \times I^{\prime} \rightarrow \mathcal{M}, \quad I, I^{\prime} \subset \mathbb{R},(s, t) \mapsto \gamma(s, t)$ be a one-parameter family of affinely parametrized geodesics. Let $\boldsymbol{T}$ be the tangent vector to the geodesic $\gamma(s=$ const, $t)$ and $\boldsymbol{S}$ be the tangent vector to the curves $\gamma(s, t=$ const $)$. Derive the equation for geodesic deviation,

  $$\nabla_{T} \nabla_{T} \boldsymbol{S}=\boldsymbol{R}(\boldsymbol{T}, \boldsymbol{S}) \boldsymbol{T}$$

  (iii) Let $X^{\alpha}$ be a unit timelike vector field $\left(X^{\mu} X_{\mu}=-1\right)$ that satisfies the geodesic equation $\nabla_{\boldsymbol{X}} \boldsymbol{X}=0$ at every point of $\mathcal{M}$. Define

  $$\begin{array}{ll} B_{\alpha \beta}:=\nabla_{\beta} X_{\alpha}, & h_{\alpha \beta}:=g_{\alpha \beta}+X_{\alpha} X_{\beta}, \\ \Theta:=B^{\alpha \beta} h_{\alpha \beta}, \quad \sigma_{\alpha \beta}:=B_{(\alpha \beta)}-\frac{1}{3} \Theta h_{\alpha \beta}, & \omega_{\alpha \beta}:=B_{[\alpha \beta]} . \end{array}$$

  Show that

  $$\begin{gathered} B_{\alpha \beta} X^{\alpha}=B_{\alpha \beta} X^{\beta}=h_{\alpha \beta} X^{\alpha}=h_{\alpha \beta} X^{\beta}=0 \\ B_{\alpha \beta}=\frac{1}{3} \Theta h_{\alpha \beta}+\sigma_{\alpha \beta}+\omega_{\alpha \beta}, \quad g^{\alpha \beta} \sigma_{\alpha \beta}=0 \end{gathered}$$

  (iv) Let $\boldsymbol{S}$ denote the geodesic deviation vector, as defined in (ii), of the family of geodesics defined by the vector field $X^{\alpha}$. Show that $\boldsymbol{S}$ satisfies

  $$X^{\mu} \nabla_{\mu} S^{\alpha}=B_{\mu}^{\alpha} S^{\mu}$$

  (v) Show that

  $$X^{\mu} \nabla_{\mu} B_{\alpha \beta}=-B_{\beta}^{\mu} B_{\alpha \mu}+R_{\mu \beta \alpha}{ }^{\nu} X^{\mu} X_{\nu}$$

  comment

Graph Theory

• Paper 1, Section II, 17G

  Graph Theory | Part II, 2020

  (a) The complement of a graph is defined as having the same vertex set as the graph, with vertices being adjacent in the complement if and only if they are not adjacent in the graph.

  Show that no planar graph of order greater than 10 has a planar complement.

  What is the maximum order of a bipartite graph that has a bipartite complement?

  (b) For the remainder of this question, let $G$ be a connected bridgeless planar graph with $n \geqslant 4$ vertices, $e$ edges, and containing no circuit of length 4 . Suppose that it is drawn with $f$ faces, of which $t$ are 3-sided.

  Show that $2 e \geqslant 3 t+5(f-t)$. Show further that $e \geqslant 3 t$, and hence $f \leqslant 8 e / 15$.

  Deduce that $e \leqslant 15(n-2) / 7$. Is there some $n$ and some $G$ for which equality holds? [Hint: consider "slicing the corners off" a dodecahedron.]

  comment

Integrable Systems

• Paper 1, Section II, 33C

  Integrable Systems | Part II, 2020

  (a) Show that if $L$ is a symmetric matrix $\left(L=L^{T}\right)$ and $B$ is skew-symmetric $\left(B=-B^{T}\right)$ then $[B, L]=B L-L B$ is symmetric.

  (b) Consider the real $n \times n$ symmetric matrix

  $$L=\left(\begin{array}{cccccccc} 0 & a_{1} & 0 & 0 & \cdots & \cdots & \cdots & 0 \\ a_{1} & 0 & a_{2} & 0 & \cdots & \cdots & \cdots & 0 \\ 0 & a_{2} & 0 & a_{3} & \cdots & \cdots & \cdots & 0 \\ 0 & 0 & a_{3} & \cdots & \cdots & \cdots & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & \cdots & \cdots & \cdots & \cdots & \cdots & a_{n-2} & 0 \\ 0 & \cdots & \cdots & \cdots & \cdots & a_{n-2} & 0 & a_{n-1} \\ 0 & \cdots & \cdots & \cdots & \cdots & 0 & a_{n-1} & 0 \end{array}\right)$$

  (i.e. $L_{i, i+1}=L_{i+1, i}=a_{i}$ for $1 \leqslant i \leqslant n-1$, all other entries being zero) and the real $n \times n$ skew-symmetric matrix

  $$B=\left(\begin{array}{cccccccc} 0 & 0 & a_{1} a_{2} & 0 & \cdots & \cdots & \cdots & 0 \\ 0 & 0 & 0 & a_{2} a_{3} & \cdots & \ldots & \ldots & 0 \\ -a_{1} a_{2} & 0 & 0 & 0 & \ldots & \ldots & \ldots & 0 \\ 0 & -a_{2} a_{3} & 0 & \ldots & \cdots & \ldots & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & \ldots & \ldots & \ldots & \ldots & \ldots & 0 & a_{n-2} a_{n-1} \\ 0 & \ldots & \cdots & \cdots & \cdots & 0 & 0 & 0 \\ 0 & \ldots & \cdots & \cdots & \ldots & -a_{n-2} a_{n-1} & 0 & 0 \end{array}\right)$$

  (i.e. $B_{i, i+2}=-B_{i+2, i}=a_{i} a_{i+1}$ for $1 \leqslant i \leqslant n-2$, all other entries being zero).

  (i) Compute $[B, L]$.

  (ii) Assume that the $a_{j}$ are smooth functions of time $t$ so the matrix $L=L(t)$ also depends smoothly on $t$. Show that the equation $\frac{d L}{d t}=[B, L]$ implies that

  $$\frac{d a_{j}}{d t}=f\left(a_{j-1}, a_{j}, a_{j+1}\right)$$

  for some function $f$ which you should find explicitly.

  (iii) Using the transformation $a_{j}=\frac{1}{2} \exp \left[\frac{1}{2} u_{j}\right]$ show that

  $$\frac{d u_{j}}{d t}=\frac{1}{2}\left(e^{u_{j+1}}-e^{u_{j-1}}\right)$$

  for $j=1, \ldots n-1$. [Use the convention $u_{0}=-\infty, a_{0}=0, u_{n}=-\infty, a_{n}=0 .$ ]

  (iv) Deduce that given a solution of equation ( $\dagger$, there exist matrices $\{U(t)\}_{t \in \mathbb{R}}$ depending on time such that $L(t)=U(t) L(0) U(t)^{-1}$, and explain how to obtain first integrals for $(t)$ from this.

  comment

Linear Analysis

• Paper 1, Section II, I

  Linear Analysis | Part II, 2020

  (a) Define the dual space $X^{*}$ of a (real) normed space $(X,\|\cdot\|)$. Define what it means for two normed spaces to be isometrically isomorphic. Prove that $\left(l_{1}\right)^{*}$ is isometrically isomorphic to $l_{\infty}$.

  (b) Let $p \in(1, \infty)$. [In this question, you may use without proof the fact that $\left(l_{p}\right)^{*}$ is isometrically isomorphic to $l_{q}$ where $\frac{1}{p}+\frac{1}{q}=1$.]

  (i) Show that if $\left\{\phi_{m}\right\}_{m=1}^{\infty}$ is a countable dense subset of $\left(l_{p}\right)^{*}$, then the function

  $$d(x, y):=\sum_{m=1}^{\infty} 2^{-m} \frac{\left|\phi_{m}(x-y)\right|}{1+\left|\phi_{m}(x-y)\right|}$$

  defines a metric on the closed unit ball $B \subset l_{p}$. Show further that for a sequence $\left\{x^{(n)}\right\}_{n=1}^{\infty}$ of elements $x^{(n)} \in B$, we have

  $$\phi\left(x^{(n)}\right) \rightarrow \phi(x) \quad \forall \phi \in\left(l_{p}\right)^{*} \quad \Leftrightarrow \quad d\left(x^{(n)}, x\right) \rightarrow 0$$

  Deduce that $(B, d)$ is a compact metric space.

  (ii) Give an example to show that for a sequence $\left\{x^{(n)}\right\}_{n=1}^{\infty}$ of elements $x^{(n)} \in B$ and $x \in B$,

  $$\phi\left(x^{(n)}\right) \rightarrow \phi(x) \quad \forall \phi \in\left(l_{p}\right)^{*} \quad \Rightarrow \quad\left\|x^{(n)}-x\right\|_{l_{p}} \rightarrow 0$$

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2020

  [Throughout this question, assume the axiom of choice.]

  Let $\kappa, \lambda$ and $\mu$ be cardinals. Define $\kappa+\lambda, \kappa \lambda$ and $\kappa^{\lambda}$. What does it mean to say $\kappa \leqslant \lambda$ ? Show that $\left(\kappa^{\lambda}\right)^{\mu}=\kappa^{\lambda \mu}$. Show also that $2^{\kappa}>\kappa$.

  Assume now that $\kappa$ and $\lambda$ are infinite. Show that $\kappa \kappa=\kappa$. Deduce that $\kappa+\lambda=\kappa \lambda=\max \{\kappa, \lambda\}$. Which of the following are always true and which can be false? Give proofs or counterexamples as appropriate. (i) $\kappa^{\lambda}=2^{\lambda}$; (ii) $\kappa \leqslant \lambda \Longrightarrow \kappa^{\lambda}=2^{\lambda}$; (iii) $\kappa^{\lambda}=\lambda^{\kappa}$.

  comment

Mathematical Biology

• Paper 1, Section I, 6B

  Mathematical Biology | Part II, 2020

  Consider a bivariate diffusion process with drift vector $A_{i}(\mathbf{x})=a_{i j} x_{j}$ and diffusion matrix $b_{i j}$ where

  $$a_{i j}=\left(\begin{array}{cc} -1 & 1 \\ -2 & -1 \end{array}\right), \quad b_{i j}=\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right)$$

  $\mathbf{x}=\left(x_{1}, x_{2}\right)$ and $i, j=1,2$.

  (i) Write down the Fokker-Planck equation for the probability $P\left(x_{1}, x_{2}, t\right)$.

  (ii) Plot the drift vector as a vector field around the origin in the region $\left|x_{1}\right|<1$, $\left|x_{2}\right|<1$.

  (iii) Obtain the stationary covariances $C_{i j}=\left\langle x_{i} x_{j}\right\rangle$ in terms of the matrices $a_{i j}$ and $b_{i j}$ and hence compute their explicit values.

  comment

Mathematics of Machine Learning

• Paper 1, Section II, J

  Mathematics of Machine Learning | Part II, 2020

  (a) Let $Z_{1}, \ldots, Z_{n}$ be i.i.d. random elements taking values in a set $\mathcal{Z}$ and let $\mathcal{F}$ be a class of functions $f: \mathcal{Z} \rightarrow \mathbb{R}$. Define the Rademacher complexity $\mathcal{R}_{n}(\mathcal{F})$. Write down an inequality relating the Rademacher complexity and

  $$\mathbb{E}\left(\sup _{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^{n}\left(f\left(Z_{i}\right)-\mathbb{E} f\left(Z_{i}\right)\right)\right)$$

  State the bounded differences inequality.

  (b) Now given i.i.d. input-output pairs $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right) \in \mathcal{X} \times\{-1,1\}$ consider performing empirical risk minimisation with misclassification loss over the class $\mathcal{H}$ of classifiers $h: \mathcal{X} \rightarrow\{-1,1\}$. Denote by $\hat{h}$ the empirical risk minimiser [which you may assume exists]. For any classifier $h$, let $R(h)$ be its misclassification risk and suppose this is minimised over $\mathcal{H}$ by $h^{*} \in \mathcal{H}$. Prove that with probability at least $1-\delta$,

  $$R(\hat{h})-R\left(h^{*}\right) \leqslant 2 \mathcal{R}_{n}(\mathcal{F})+\sqrt{\frac{2 \log (2 / \delta)}{n}}$$

  for $\delta \in(0,1]$, where $\mathcal{F}$ is a class of functions $f: \mathcal{X} \times\{-1,1\} \rightarrow\{0,1\}$ related to $\mathcal{H}$ that you should specify.

  (c) Let $Z_{i}=\left(X_{i}, Y_{i}\right)$ for $i=1, \ldots, n$. Define the empirical Rademacher complexity $\hat{\mathcal{R}}\left(\mathcal{F}\left(Z_{1: n}\right)\right)$. Show that with probability at least $1-\delta$,

  $$R(\hat{h})-R\left(h^{*}\right) \leqslant 2 \hat{\mathcal{R}}\left(\mathcal{F}\left(Z_{1: n}\right)\right)+2 \sqrt{\frac{2 \log (3 / \delta)}{n}}$$

  comment

Number Fields

• Paper 1, Section II, 20G

  Number Fields | Part II, 2020

  State Minkowski's theorem.

  Let $K=\mathbb{Q}(\sqrt{-d})$, where $d$ is a square-free positive integer, not congruent to 3 $(\bmod 4) .$ Show that every nonzero ideal $I \subset \mathcal{O}_{K}$ contains an element $\alpha$ with

  $$0<\left|N_{K / \mathbb{Q}}(\alpha)\right| \leqslant \frac{4 \sqrt{d}}{\pi} N(I)$$

  Deduce the finiteness of the class group of $K$.

  Compute the class group of $\mathbb{Q}(\sqrt{-22})$. Hence show that the equation $y^{3}=x^{2}+22$ has no integer solutions.

  comment

Number Theory

• Paper 1, Section I, H

  Number Theory | Part II, 2020

  What does it mean to say that a positive definite binary quadratic form is reduced?

  Find all reduced binary quadratic forms of discriminant $-20$.

  Prove that if a prime $p \neq 5$ is represented by $x^{2}+5 y^{2}$, then $p \equiv 1,3,7$ or $9 \bmod 20$.

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2020

  Let $A \in \mathbb{R}^{n \times n}$ be a real symmetric matrix with distinct eigenvalues $\lambda_{1}<\lambda_{2}<\cdots<$ $\lambda_{n}$ and a corresponding orthonormal basis of real eigenvectors $\left\{\boldsymbol{w}_{i}\right\}_{i=1}^{n}$. Given a unit norm vector $\boldsymbol{x}^{(0)} \in \mathbb{R}^{n}$, and a set of parameters $s_{k} \in \mathbb{R}$, consider the inverse iteration algorithm

  $$\left(A-s_{k} I\right) \boldsymbol{y}=\boldsymbol{x}^{(k)}, \quad \boldsymbol{x}^{(k+1)}=\boldsymbol{y} /\|\boldsymbol{y}\|, \quad k \geqslant 0 .$$

  (a) Let $s_{k}=s=$ const for all $k$. Assuming that $\boldsymbol{x}^{(0)}=\sum_{i=1}^{n} c_{i} \boldsymbol{w}_{i}$ with all $c_{i} \neq 0$, prove that

  $$s<\lambda_{1} \Rightarrow \boldsymbol{x}^{(k)} \rightarrow \boldsymbol{w}_{1} \quad \text { or } \quad \boldsymbol{x}^{(k)} \rightarrow-\boldsymbol{w}_{1} \quad(k \rightarrow \infty) .$$

  Explain briefly what happens to $\boldsymbol{x}^{(k)}$ when $\lambda_{m}<s<\lambda_{m+1}$ for some $m \in\{1,2, \ldots, n-1\}$, and when $\lambda_{n}<s$.

  (b) Let $s_{k}=\left(A \boldsymbol{x}^{(k)}, \boldsymbol{x}^{(k)}\right)$ for $k \geqslant 0$. Assuming that, for some $k$, some $a_{i} \in \mathbb{R}$ and for a small $\epsilon$,

  $$\boldsymbol{x}^{(k)}=c^{-1}\left(\boldsymbol{w}_{1}+\epsilon \sum_{i \geqslant 2} a_{i} \boldsymbol{w}_{i}\right)$$

  where $c$ is the appropriate normalising constant. Show that $s_{k}=\lambda_{1}-K \epsilon^{2}+\mathcal{O}\left(\epsilon^{4}\right)$ and determine the value of $K$. Hence show that

  $$\boldsymbol{x}^{(k+1)}=c_{1}^{-1}\left(\boldsymbol{w}_{1}+\epsilon^{3} \sum_{i \geqslant 2} b_{i} \boldsymbol{w}_{i}+\mathcal{O}\left(\epsilon^{5}\right)\right)$$

  where $c_{1}$ is the appropriate normalising constant, and find expressions for $b_{i}$.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, A

  Principles of Quantum Mechanics | Part II, 2020

  Let $A=(m \omega X+i P) / \sqrt{2 m \hbar \omega}$ be the lowering operator of a one dimensional quantum harmonic oscillator of mass $m$ and frequency $\omega$, and let $|0\rangle$ be the ground state defined by $A|0\rangle=0$.

  a) Evaluate the commutator $\left[A, A^{\dagger}\right]$.

  b) For $\gamma \in \mathbb{R}$, let $S(\gamma)$ be the unitary operator $S(\gamma)=\exp \left(-\frac{\gamma}{2}\left(A^{\dagger} A^{\dagger}-A A\right)\right)$ and define $A(\gamma)=S^{\dagger}(\gamma) A S(\gamma)$. By differentiating with respect to $\gamma$ or otherwise, show that

  $$A(\gamma)=A \cosh \gamma-A^{\dagger} \sinh \gamma$$

  c) The ground state of the harmonic oscillator saturates the uncertainty relation $\Delta X \Delta P \geqslant \hbar / 2$. Compute $\Delta X \Delta P$ when the oscillator is in the state $|\gamma\rangle=S(\gamma)|0\rangle$.

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2020

  State and prove the Cramér-Rao inequality for a real-valued parameter $\theta$. [Necessary regularity conditions need not be stated.]

  In a general decision problem, define what it means for a decision rule to be minimax.

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. from a $N(\theta, 1)$ distribution, where $\theta \in \Theta=[0, \infty)$. Prove carefully that $\bar{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$ is minimax for quadratic risk on $\Theta$.

  comment

Probability and Measure

• Paper 1, Section II, 27K

  Probability and Measure | Part II, 2020

  (a) Let $(X, \mathcal{F}, \nu)$ be a probability space. State the definition of the space $\mathbb{L}^{2}(X, \mathcal{F}, \nu)$. Show that it is a Hilbert space.

  (b) Give an example of two real random variables $Z_{1}, Z_{2}$ that are not independent and yet have the same law.

  (c) Let $Z_{1}, \ldots, Z_{n}$ be $n$ random variables distributed uniformly on $[0,1]$. Let $\lambda$ be the Lebesgue measure on the interval $[0,1]$, and let $\mathcal{B}$ be the Borel $\sigma$-algebra. Consider the expression

  $$D(f):=\operatorname{Var}\left[\frac{1}{n}\left(f\left(Z_{1}\right)+\ldots+f\left(Z_{n}\right)\right)-\int_{[0,1]} f d \lambda\right]$$

  where Var denotes the variance and $f \in \mathbb{L}^{2}([0,1], \mathcal{B}, \lambda)$.

  Assume that $Z_{1}, \ldots, Z_{n}$ are pairwise independent. Compute $D(f)$ in terms of the variance $\operatorname{Var}(f):=\operatorname{Var}\left(f\left(Z_{1}\right)\right)$.

  (d) Now we no longer assume that $Z_{1}, \ldots, Z_{n}$ are pairwise independent. Show that

  $$\sup D(f) \geqslant \frac{1}{n},$$

  where the supremum ranges over functions $f \in \mathbb{L}^{2}([0,1], \mathcal{B}, \lambda)$ such that $\|f\|_{2}=1$ and $\int_{[0,1]} f d \lambda=0$.

  [Hint: you may wish to compute $D\left(f_{p, q}\right)$ for the family of functions $f_{p, q}=\sqrt{\frac{k}{2}}\left(1_{I_{p}}-1_{I_{q}}\right)$ where $1 \leqslant p, q \leqslant k, I_{j}=\left[\frac{j}{k}, \frac{j+1}{k}\right)$ and $1_{A}$ denotes the indicator function of the subset $\left.A .\right]$

  comment

Quantum Information and Computation

• Paper 1, Section I, 10C

  Quantum Information and Computation | Part II, 2020

  Suppose we measure an observable $A=\hat{n} \cdot \vec{\sigma}$on a qubit, where $\hat{n}=\left(n_{x}, n_{y}, n_{z}\right) \in \mathbb{R}^{3}$ is a unit vector and $\vec{\sigma}=\left(\sigma_{x}, \sigma_{y}, \sigma_{z}\right)$ is the vector of Pauli operators.

  (i) Express $A$ as a $2 \times 2$ matrix in terms of the components of $\hat{n}$.

  (ii) Representing $\hat{n}$ in terms of spherical polar coordinates as $\hat{n}=(1, \theta, \phi)$, rewrite the above matrix in terms of the angles $\theta$ and $\phi$.

  (iii) What are the possible outcomes of the above measurement?

  (iv) Suppose the qubit is initially in a state $|1\rangle$. What is the probability of getting an outcome 1?

  (v) Consider the three-qubit state

  $$|\psi\rangle=a|000\rangle+b|010\rangle+c|110\rangle+d|111\rangle+e|100\rangle$$

  Suppose the second qubit is measured relative to the computational basis. What is the probability of getting an outcome 1? State the rule that you are using.

  comment

Representation Theory

• Paper 1, Section II, F

  Representation Theory | Part II, 2020

  State and prove Maschke's theorem.

  Let $G$ be the group of isometries of $\mathbb{Z}$. Recall that $G$ is generated by the elements $t, s$ where $t(n)=n+1$ and $s(n)=-n$ for $n \in \mathbb{Z}$.

  Show that every non-faithful finite-dimensional complex representation of $G$ is a direct sum of subrepresentations of dimension at most two.

  Write down a finite-dimensional complex representation of the group $(\mathbb{Z},+)$ that is not a direct sum of one-dimensional subrepresentations. Hence, or otherwise, find a finitedimensional complex representation of $G$ that is not a direct sum of subrepresentations of dimension at most two. Briefly justify your answer.

  [Hint: You may assume that any non-trivial normal subgroup of $G$ contains an element of the form $t^{m}$ for some $m>0$.]

  comment

Riemann Surfaces

• Paper 1, Section II, 24F

  Riemann Surfaces | Part II, 2020

  Assuming any facts about triangulations that you need, prove the Riemann-Hurwitz theorem.

  Use the Riemann-Hurwitz theorem to prove that, for any cubic polynomial $f: \mathbb{C} \rightarrow \mathbb{C}$, there are affine transformations $g(z)=a z+b$ and $h(z)=c z+d$ such that $k(z)=g \circ f \circ h(z)$ is of one of the following two forms:

  $$k(z)=z^{3} \text { or } k(z)=z\left(z^{2} / 3-1\right)$$

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2020

  Consider a generalised linear model with full column rank design matrix $X \in \mathbb{R}^{n \times p}$, output variables $Y=\left(Y_{1}, \ldots, Y_{n}\right) \in \mathbb{R}^{n}$, link function $g$, mean parameters $\mu=\left(\mu_{1}, \ldots, \mu_{n}\right)$ and known dispersion parameters $\sigma_{i}^{2}=a_{i} \sigma^{2}, i=1, \ldots, n$. Denote its variance function by $V$ and recall that $g\left(\mu_{i}\right)=x_{i}^{T} \beta, i=1, \ldots, n$, where $\beta \in \mathbb{R}^{p}$ and $x_{i}^{T}$ is the $i^{\text {th }}$row of $X$.

  (a) Define the score function in terms of the log-likelihood function and the Fisher information matrix, and define the update of the Fisher scoring algorithm.

  (b) Let $W \in \mathbb{R}^{n \times n}$ be a diagonal matrix with positive entries. Note that $X^{T} W X$ is invertible. Show that

  $$\operatorname{argmin}_{b \in \mathbb{R}^{p}}\left\{\sum_{i=1}^{n} W_{i i}\left(Y_{i}-x_{i}^{T} b\right)^{2}\right\}=\left(X^{T} W X\right)^{-1} X^{T} W Y$$

  [Hint: you may use that $\left.\operatorname{argmin}_{b \in \mathbb{R}^{p}}\left\{\left\|Y-X^{T} b\right\|^{2}\right\}=\left(X^{T} X\right)^{-1} X^{T} Y .\right]$

  (c) Recall that the score function and the Fisher information matrix have entries

  $$\begin{aligned} &U_{j}(\beta)=\sum_{i=1}^{n} \frac{\left(Y_{i}-\mu_{i}\right) X_{i j}}{a_{i} \sigma^{2} V\left(\mu_{i}\right) g^{\prime}\left(\mu_{i}\right)} \quad j=1, \ldots, p \\ &i_{j k}(\beta)=\sum_{i=1}^{n} \frac{X_{i j} X_{i k}}{a_{i} \sigma^{2} V\left(\mu_{i}\right)\left\{g^{\prime}\left(\mu_{i}\right)\right\}^{2}} \quad j, k=1, \ldots, p \end{aligned}$$

  Justify, performing the necessary calculations and using part (b), why the Fisher scoring algorithm is also known as the iterative reweighted least squares algorithm.

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2020

  We consider a subset of the data on car insurance claims from Hallin and Ingenbleek (1983). For each customer, the dataset includes total payments made per policy-year, the amount of kilometres driven, the bonus from not having made previous claims, and the brand of the car. The amount of kilometres driven is a factor taking values $1,2,3,4$, or 5 , where a car in level $i+1$ has driven a larger number of kilometres than a car in level $i$ for any $i=1,2,3,4$. A statistician from an insurance company fits the following model on $R$.

  $>$ model1 <- Im(Paymentperpolicyyr as numeric(Kilometres) $+$ Brand $+$ Bonus)

  (i) Why do you think the statistician transformed variable Kilometres from a factor to a numerical variable?

  (ii) To check the quality of the model, the statistician applies a function to model1 which returns the following figure:

  

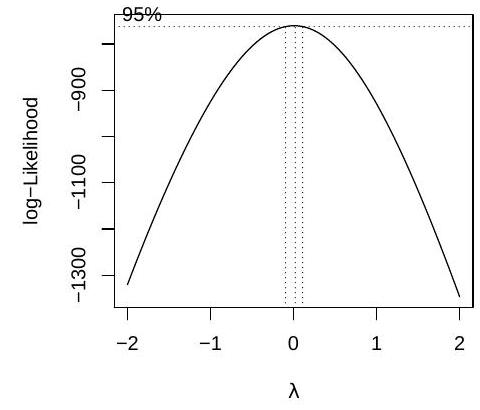
  What does the plot represent? Does it suggest that model1 is a good model? Explain. If not, write down a model which the plot suggests could be better.

  (iii) The statistician fits the model suggested by the graph and calls it model2. Consider the following abbreviated output:

  $>\operatorname{summary}(\operatorname{model2})$

  $\cdots$

  Coefficients:

  $\begin{array}{lrrrr}\text { (Intercept) } & 6.514035 & 0.186339 & 34.958 & <2 \mathrm{e}-16 * * * \\ \text { as.numeric(Kilometres) } & 0.057132 & 0.032654 & 1.750 & 0.08126 . \\ \text { Brand2 } & 0.363869 & 0.186857 & 1.947 & 0.05248 .\end{array}$

  Brand2

  $\cdots$

  Brand9

  $\begin{array}{lllll}0.125446 & 0.186857 & 0.671 & 0.50254\end{array}$

  Bonus

  

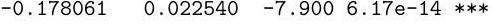
  Signif. codes: 0 '' $0.001$ '' $0.01$ '' $0.05$ '.' $0.1$ ' 1

  Residual standard error: $0.7817$ on 284 degrees of freedom ..

  Using the output, write down a $95 \%$ prediction interval for the ratio between the total payments per policy year for two cars of the same brand and with the same value of Bonus, one of which has a Kilometres value one higher than the other. You may express your answer as a function of quantiles of a common distribution, which you should specify.

  (iv) Write down a generalised linear model for Paymentperpolicyyr which may be a better model than model1 and give two reasons. You must specify the link function.

  comment

Statistical Physics

• Paper 1, Section II, A

  Statistical Physics | Part II, 2020

  Using the notion of entropy, show that two systems that can freely exchange energy reach the same temperature. Show that the energy of a system increases with temperature.

  A system consists of $N$ distinguishable, non-interacting spin $\frac{1}{2}$ atoms in a magnetic field, where $N$ is large. The energy of an atom is $\varepsilon>0$ if the spin is up and $-\varepsilon$ if the spin is down. Find the entropy and energy if a fraction $\alpha$ of the atoms have spin up. Determine $\alpha$ as a function of temperature, and deduce the allowed range of $\alpha$. Verify that the energy of the system increases with temperature in this range.

  comment

Stochastic Financial Models

• Paper 1, Section II, 30K

  Stochastic Financial Models | Part II, 2020

  Consider a single-period asset price model $\left(\bar{S}_{0}, \bar{S}_{1}\right)$ in $\mathbb{R}^{d+1}$ where, for $n=0,1$,

  $$\bar{S}_{n}=\left(S_{n}^{0}, S_{n}\right)=\left(S_{n}^{0}, S_{n}^{1}, \ldots, S_{n}^{d}\right)$$

  with $S_{0}$ a non-random vector in $\mathbb{R}^{d}$ and

  $$S_{0}^{0}=1, \quad S_{1}^{0}=1+r, \quad S_{1} \sim N(\mu, V) .$$

  Assume that $V$ is invertible. An investor has initial wealth $w_{0}$ which is invested in the market at time 0 , to hold $\theta^{0}$ units of the riskless asset $S^{0}$ and $\theta^{i}$ units of risky asset $i$, for $i=1, \ldots, d$.

  (a) Show that in order to minimize the variance of the wealth $\bar{\theta} \cdot \bar{S}_{1}$ held at time 1 , subject to the constraint

  $$\mathbb{E}\left(\bar{\theta} \cdot \bar{S}_{1}\right)=w_{1}$$

  with $w_{1}$ given, the investor should choose a portfolio of the form

  $$\theta=\lambda \theta_{m}, \quad \theta_{m}=V^{-1}\left(\mu-(1+r) S_{0}\right)$$

  where $\lambda$ is to be determined.

  (b) Show that the same portfolio is optimal for a utility-maximizing investor with CARA utility function

  $$U(x)=-\exp \{-\gamma x\}$$

  for a unique choice of $\gamma$, also to be determined.

  comment

Topics in Analysis

• Paper 1, Section I, $\mathbf{2 H}$

  Topics in Analysis | Part II, 2020

  Let $\gamma:[0,1] \rightarrow \mathbb{C}$ be a continuous map never taking the value 0 and satisfying $\gamma(0)=\gamma(1)$. Define the degree (or winding number) $w(\gamma ; 0)$ of $\gamma$ about 0 . Prove the following.

  (i) If $\delta:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ is a continuous map satisfying $\delta(0)=\delta(1)$, then the winding number of the product $\gamma \delta$ is given by $w(\gamma \delta ; 0)=w(\gamma ; 0)+w(\delta ; 0)$.

  (ii) If $\sigma:[0,1] \rightarrow \mathbb{C}$ is continuous, $\sigma(0)=\sigma(1)$ and $|\sigma(t)|<|\gamma(t)|$ for each $0 \leqslant t \leqslant 1$, then $w(\gamma+\sigma ; 0)=w(\gamma ; 0)$.

  (iii) Let $D=\{z \in \mathbb{C}:|z| \leqslant 1\}$ and let $f: D \rightarrow \mathbb{C}$ be a continuous function with $f(z) \neq 0$ whenever $|z|=1$. Define $\alpha:[0,1] \rightarrow \mathbb{C}$ by $\alpha(t)=f\left(e^{2 \pi i t}\right)$. Then if $w(\alpha ; 0) \neq 0$, there must exist some $z \in D$, such that $f(z)=0$. [It may help to define $F(s, t):=f\left(s e^{2 \pi i t}\right)$. Homotopy invariance of the winding number may be assumed.]

  comment

Waves

• Paper 1, Section II, B

  Waves | Part II, 2020

  (a) Write down the linearised equations governing motion of an inviscid compressible fluid at uniform entropy. Assuming that the velocity is irrotational, show that the velocity potential $\phi(\mathbf{x}, t)$ satisfies the wave equation and identify the wave speed $c_{0}$. Obtain from these linearised equations the energy-conservation equation

  $$\frac{\partial E}{\partial t}+\nabla \cdot \mathbf{I}=0$$

  and give expressions for the acoustic-energy density $E$ and the acoustic-energy flux, or intensity, I.

  (b) Inviscid compressible fluid with density $\rho_{0}$ and sound speed $c_{0}$ occupies the regions $y<0$ and $y>0$, which are separated by a thin elastic membrane at an undisturbed position $y=0$. The membrane has mass per unit area $m$ and is under a constant tension $T$. Small displacements of the membrane to $y=\eta(x, t)$ are coupled to small acoustic disturbances in the fluid with velocity potential $\phi(x, y, t)$.

  (i) Write down the (linearised) kinematic and dynamic boundary conditions at the membrane. [Hint: The elastic restoring force on the membrane is like that on a stretched string.]

  (ii) Show that the dispersion relation for waves proportional to $\cos (k x-\omega t)$ propagating along the membrane with $|\phi| \rightarrow 0$ as $y \rightarrow \pm \infty$ is given by

  $$\left\{m+\frac{2 \rho_{0}}{\left(k^{2}-\omega^{2} / c_{0}^{2}\right)^{1 / 2}}\right\} \omega^{2}=T k^{2}$$

  Interpret this equation by explaining physically why all disturbances propagate with phase speed $c$ less than $(T / m)^{1 / 2}$ and why $c(k) \rightarrow 0$ as $k \rightarrow 0$.

  (iii) Show that in such a wave the component $\left\langle I_{y}\right\rangle$ of mean acoustic intensity perpendicular to the membrane is zero.

  comment