Part II, 2017, Paper 2

Algebraic Geometry

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2017

  Let $k$ be an algebraically closed field of any characteristic.

  (a) Define what it means for a variety $X$ to be non-singular at a point $P \in X$.

  (b) Let $X \subseteq \mathbb{P}^{n}$ be a hypersurface $Z(f)$ for $f \in k\left[x_{0}, \ldots, x_{n}\right]$ an irreducible homogeneous polynomial. Show that the set of singular points of $X$ is $Z(I)$, where $I \subseteq$ $k\left[x_{0}, \ldots, x_{n}\right]$ is the ideal generated by $\partial f / \partial x_{0}, \ldots, \partial f / \partial x_{n} .$

  (c) Consider the projective plane curve corresponding to the affine curve in $\mathbb{A}^{2}$ given by the equation

  $$x^{4}+x^{2} y^{2}+y^{2}+1=0 .$$

  Find the singular points of this projective curve if char $k \neq 2$. What goes wrong if char $k=2$ ?

  comment

Algebraic Topology

• Paper 2, Section II, I

  Algebraic Topology | Part II, 2017

  (a) (i) Define the push-out of the following diagram of groups.

  

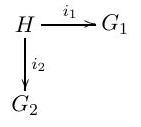
  When is a push-out a free product with amalgamation?

  (ii) State the Seifert-van Kampen theorem.

  (b) Let $X=\mathbb{R} P^{2} \vee S^{1}$ (recalling that $\mathbb{R} P^{2}$ is the real projective plane), and let $x \in X$.

  (i) Compute the fundamental group $\pi_{1}(X, x)$ of the space $X$.

  (ii) Show that there is a surjective homomorphism $\phi: \pi_{1}(X, x) \rightarrow S_{3}$, where $S_{3}$ is the symmetric group on three elements.

  (c) Let $\widehat{X} \rightarrow X$ be the covering space corresponding to the kernel of $\phi$.

  (i) Draw $\widehat{X}$and justify your answer carefully.

  (ii) Does $\widehat{X}$retract to a graph? Justify your answer briefly.

  (iii) Does $\widehat{X}$deformation retract to a graph? Justify your answer briefly.

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  Give an account of the variational method for establishing an upper bound on the ground-state energy of a Hamiltonian $H$ with a discrete spectrum $H|n\rangle=E_{n}|n\rangle$, where $E_{n} \leqslant E_{n+1}, n=0,1,2 \ldots$

  A particle of mass $m$ moves in the three-dimensional potential

  $$V(r)=-\frac{A e^{-\mu r}}{r}$$

  where $A, \mu>0$ are constants and $r$ is the distance to the origin. Using the normalised variational wavefunction

  $$\psi(r)=\sqrt{\frac{\alpha^{3}}{\pi}} e^{-\alpha r}$$

  show that the expected energy is given by

  $$E(\alpha)=\frac{\hbar^{2} \alpha^{2}}{2 m}-\frac{4 A \alpha^{3}}{(\mu+2 \alpha)^{2}}$$

  Explain why there is necessarily a bound state when $\mu<A m / \hbar^{2}$. What can you say about the existence of a bound state when $\mu \geqslant A m / \hbar^{2}$ ?

  [Hint: The Laplacian in spherical polar coordinates is

  $$\left.\nabla^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \phi^{2}}\right]$$

  comment

Applied Probability

• Paper 2, Section II, K

  Applied Probability | Part II, 2017

  (a) Give the definition of a Poisson process on $\mathbb{R}_{+}$. Let $X$ be a Poisson process on $\mathbb{R}_{+}$. Show that conditional on $\left\{X_{t}=n\right\}$, the jump times $J_{1}, \ldots, J_{n}$ have joint density function

  $$f\left(t_{1}, \ldots, t_{n}\right)=\frac{n !}{t^{n}} \mathbf{1}\left(0 \leqslant t_{1} \leqslant \ldots \leqslant t_{n} \leqslant t\right)$$

  where $\boldsymbol{I}(A)$ is the indicator of the set $A$.

  (b) Let $N$ be a Poisson process on $\mathbb{R}_{+}$with intensity $\lambda$ and jump times $\left\{J_{k}\right\}$. If $g: \mathbb{R}_{+} \rightarrow \mathbb{R}$ is a real function, we define for all $t>0$

  $$\mathcal{R}(g)[0, t]=\left\{g\left(J_{k}\right): k \in \mathbb{N}, J_{k} \leqslant t\right\}$$

  Show that for all $t>0$ the following is true

  $$\mathbb{P}(0 \in \mathcal{R}(g)[0, t])=1-\exp \left(-\lambda \int_{0}^{t} \mathbf{I}(g(s)=0) d s\right)$$

  comment

Asymptotic Methods

• Paper 2, Section II, E

  Asymptotic Methods | Part II, 2017

  Consider the function

  $$f_{\nu}(x) \equiv \frac{1}{2 \pi} \int_{C} \exp [-i x \sin z+i \nu z] d z$$

  where the contour $C$ is the boundary of the half-strip $\{z:-\pi<\operatorname{Re} z<\pi$ and $\operatorname{Im} z>0\}$, taken anti-clockwise.

  Use integration by parts and the method of stationary phase to:

  (i) Obtain the leading term for $f_{\nu}(x)$ coming from the vertical lines $z=\pm \pi+i y(0<$ $y<+\infty)$ for large $x>0$.

  (ii) Show that the leading term in the asymptotic expansion of the function $f_{\nu}(x)$ for large positive $x$ is

  $$\sqrt{\frac{2}{\pi x}} \cos \left(x-\frac{1}{2} \nu \pi-\frac{\pi}{4}\right)$$

  and obtain an estimate for the remainder as $O\left(x^{-a}\right)$ for some $a$ to be determined.

  comment

Automata and Formal Languages

• Paper 2, Section I, $4 \mathrm{H}$

  Automata and Formal Languages | Part II, 2017

  (a) Give explicit examples, with justification, of a language over some finite alphabet $\Sigma$ which is:

  (i) context-free, but not regular;

  (ii) recursive, but not context-free.

  (b) Give explicit examples, with justification, of a subset of $\mathbb{N}$ which is:

  (i) recursively enumerable, but not recursive;

  (ii) neither recursively enumerable, nor having recursively enumerable complement in $\mathbb{N}$.

  comment

Classical Dynamics

• Paper 2, Section I, E

  Classical Dynamics | Part II, 2017

  Derive the Lagrange equations from the principle of stationary action

  $$S[q]=\int_{t_{0}}^{t_{1}} \mathcal{L}\left(q_{i}(t), \dot{q}_{i}(t), t\right) d t, \quad \delta S=0$$

  where the end points $q_{i}\left(t_{0}\right)$ and $q_{i}\left(t_{1}\right)$ are fixed.

  Let $\phi$ and $\mathbf{A}$ be a scalar and a vector, respectively, depending on $\mathbf{r}=(x, y, z)$. Consider the Lagrangian

  $$\mathcal{L}=\frac{m \dot{\mathbf{r}}^{2}}{2}-(\phi-\dot{\mathbf{r}} \cdot \mathbf{A})$$

  and show that the resulting Euler-Lagrange equations are invariant under the transformations

  $$\phi \rightarrow \phi+\alpha \frac{\partial F}{\partial t}, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla F,$$

  where $F=F(\mathbf{r}, t)$ is an arbitrary function, and $\alpha$ is a constant which should be determined.

  comment

• Paper 2, Section II, E

  Classical Dynamics | Part II, 2017

  Show that an object's inertia tensor about a point displaced from the centre of mass by a vector $\mathbf{c}$ is given by

  $$\left(I_{\mathbf{c}}\right)_{a b}=\left(I_{0}\right)_{a b}+M\left(|\mathbf{c}|^{2} \delta_{a b}-c_{a} c_{b}\right),$$

  where $M$ is the total mass of the object, and $\left(I_{0}\right)_{a b}$ is the inertia tensor about the centre of mass.

  Find the inertia tensor of a cube of uniform density, with edge of length $L$, about one of its vertices.

  comment

Coding and Cryptography

• Paper 2, Section I, G

  Coding and Cryptography | Part II, 2017

  Prove that a decipherable code with prescribed word lengths exists if and only if there is a prefix-free code with the same word lengths.

  comment

• Paper 2, Section II, G

  Coding and Cryptography | Part II, 2017

  Define the entropy, $H(X)$, of a random variable $X$. State and prove Gibbs' inequality.

  Hence, or otherwise, show that $H\left(p_{1}, p_{2}, p_{3}\right) \leqslant H\left(p_{1}, 1-p_{1}\right)+\left(1-p_{1}\right)$ and determine when equality occurs.

  Show that the Discrete Memoryless Channel with channel matrix

  $$\left(\begin{array}{ccc} 1-\alpha-\beta & \alpha & \beta \\ \alpha & 1-\alpha-\beta & \beta \end{array}\right)$$

  has capacity $C=(1-\beta)(1-\log (1-\beta))+(1-\alpha-\beta) \log (1-\alpha-\beta)+\alpha \log \alpha$.

  comment

Cosmology

• Paper 2, Section I, C

  Cosmology | Part II, 2017

  In a homogeneous and isotropic universe $(\Lambda=0)$, the acceleration equation for the scale factor $a(t)$ is given by

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right),$$

  where $\rho(t)$ is the mass density and $P(t)$ is the pressure.

  If the matter content of the universe obeys the strong energy condition $\rho+3 P / c^{2} \geqslant 0$, show that the acceleration equation can be rewritten as $\dot{H}+H^{2} \leqslant 0$, with Hubble parameter $H(t)=\dot{a} / a$. Show that

  $$H \geqslant \frac{1}{H_{0}^{-1}+t-t_{0}}$$

  where $H_{0}=H\left(t_{0}\right)$ is the measured value today at $t=t_{0}$. Hence, or otherwise, show that

  $$a(t) \leqslant 1+H_{0}\left(t-t_{0}\right)$$

  Use this inequality to find an upper bound on the age of the universe.

  comment

Differential Geometry

• Paper 2, Section II, I

  Differential Geometry | Part II, 2017

  Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a regular smooth curve. Define the curvature $k$ and torsion $\tau$ of $\alpha$ and derive the Frenet formulae. Give the assumption which must hold for torsion to be well-defined, and state the Fundamental Theorem for curves in $\mathbb{R}^{3}$.

  Let $\alpha$ be as above and $\tilde{\alpha}: I \rightarrow \mathbb{R}^{3}$ be another regular smooth curve with curvature $\tilde{k}$ and torsion $\tilde{\tau}$. Suppose $\tilde{k}(s)=k(s) \neq 0$ and $\tilde{\tau}(s)=\tau(s)$ for all $s \in I$, and that there exists a non-empty open subinterval $J \subset I$ such that $\left.\tilde{\alpha}\right|_{J}=\left.\alpha\right|_{J}$. Show that $\tilde{\alpha}=\alpha$.

  Now let $S \subset \mathbb{R}^{3}$ be an oriented surface and let $\alpha: I \rightarrow S \subset \mathbb{R}^{3}$ be a regular smooth curve contained in $S$. Define normal curvature and geodesic curvature. When is $\alpha$ a geodesic? Give an example of a surface $S$ and a geodesic $\alpha$ whose normal curvature vanishes identically. Must such a surface $S$ contain a piece of a plane? Can such a geodesic be a simple closed curve? Justify your answers.

  Show that if $\alpha$ is a geodesic and the Gaussian curvature of $S$ satisfies $K \geqslant 0$, then we have the inequality $k(s) \leqslant 2|H(\alpha(s))|$, where $H$ denotes the mean curvature of $S$ and $k$ the curvature of $\alpha$. Give an example where this inequality is sharp.

  comment

Dynamical Systems

• Paper 2, Section II, A

  Dynamical Systems | Part II, 2017

  (a) State Liapunov's first theorem and La Salle's invariance principle. Use these results to show that the fixed point at the origin of the system

  $$\ddot{x}+k \dot{x}+\sin ^{3} x=0, \quad k>0,$$

  is asymptotically stable.

  (b) State the Poincaré-Bendixson theorem. Show that the forced damped pendulum

  $$\dot{\theta}=p, \quad \dot{p}=-k p-\sin \theta+F, \quad k>0,$$

  with $F>1$, has a periodic orbit that encircles the cylindrical phase space $(\theta, p) \in \mathbb{R}[\bmod 2 \pi] \times \mathbb{R}$, and that it is unique.

  [You may assume that the Poincaré-Bendixson theorem also holds on a cylinder, and comment, without proof, on the use of any other standard results.]

  (c) Now consider $(*)$ for $F, k=O(\epsilon)$, where $\epsilon \ll 1$. Use the energy-balance method to show that there is a homoclinic orbit in $p \geqslant 0$ if $F=F_{h}(k)$, where $F_{h} \approx 4 k / \pi>0$.

  Explain briefly why there is no homoclinic orbit in $p \leqslant 0$ for $F>0$.

  comment

Fluid Dynamics II

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2017

  A cylinder of radius $a$ falls at speed $U$ without rotating through viscous fluid adjacent to a vertical plane wall, with its axis horizontal and parallel to the wall. The distance between the cylinder and the wall is $h_{0} \ll a$. Use lubrication theory in a frame of reference moving with the cylinder to determine that the two-dimensional volume flux between the cylinder and the wall is

  $$q=\frac{2 h_{0} U}{3}$$

  upwards, relative to the cylinder.

  Determine an expression for the viscous shear stress on the cylinder. Use this to calculate the viscous force and hence the torque on the cylinder. If the cylinder is free to rotate, what does your result say about the sense of rotation of the cylinder?

  [Hint: You may quote the following integrals:

  $$\left.\int_{-\infty}^{\infty} \frac{d t}{1+t^{2}}=\pi, \quad \int_{-\infty}^{\infty} \frac{d t}{\left(1+t^{2}\right)^{2}}=\frac{\pi}{2}, \quad \int_{-\infty}^{\infty} \frac{d t}{\left(1+t^{2}\right)^{3}}=\frac{3 \pi}{8}\right]$$

  comment

Further Complex Methods

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2017

  Euler's formula for the Gamma function is

  $$\Gamma(z)=\frac{1}{z} \prod_{n=1}^{\infty}\left(1+\frac{1}{n}\right)^{z}\left(1+\frac{z}{n}\right)^{-1}$$

  Use Euler's formula to show

  $$\frac{\Gamma(2 z)}{2^{2 z} \Gamma(z) \Gamma\left(z+\frac{1}{2}\right)}=C$$

  where $C$ is a constant.

  Evaluate $C$.

  [Hint: You may use $\Gamma(z) \Gamma(1-z)=\pi / \sin (\pi z) .]$

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2017

  The hypergeometric equation is represented by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & 1 & \infty \\ 0 & 0 & a \\ 1-c & c-a-b & b \end{array}\right\}$$

  and has solution $y_{0}(z)=F(a, b, c ; z)$.

  Functions $y_{1}(z)$ and $y_{2}(z)$ are defined by

  $$y_{1}(z)=F(a, b, a+b+1-c ; 1-z)$$

  and

  $$y_{2}(z)=(1-z)^{c-a-b} F(c-a, c-b, c-a-b+1 ; 1-z),$$

  where $c-a-b$ is not an integer.

  Show that $y_{1}(z)$ and $y_{2}(z)$ obey the hypergeometric equation $(*)$.

  Explain why $y_{0}(z)$ can be written in the form

  $$y_{0}(z)=A y_{1}(z)+B y_{2}(z)$$

  where $A$ and $B$ are independent of $z$ but depend on $a, b$ and $c$.

  Suppose that

  $$F(a, b, c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  with $\operatorname{Re}(c)>\operatorname{Re}(b)>0$ and $|\arg (1-z)|<\pi$. Find expressions for $A$ and $B$.

  comment

Galois Theory

• Paper 2, Section II, I

  Galois Theory | Part II, 2017

  (a) Define what it means for a finite field extension $L$ of a field $K$ to be separable. Show that $L$ is of the form $K(\alpha)$ for some $\alpha \in L$.

  (b) Let $p$ and $q$ be distinct prime numbers. Let $L=\mathbb{Q}(\sqrt{p}, \sqrt{-q})$. Express $L$ in the form $\mathbb{Q}(\alpha)$ and find the minimal polynomial of $\alpha$ over $\mathbb{Q}$.

  (c) Give an example of a field extension $K \leqslant L$ of finite degree, where $L$ is not of the form $K(\alpha)$. Justify your answer.

  comment

General Relativity

• Paper 2, Section II, D

  General Relativity | Part II, 2017

  (a) The Friedmann-Robertson-Walker metric is given by

  $$d s^{2}=-d t^{2}+a^{2}(t)\left[\frac{d r^{2}}{1-k r^{2}}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  where $k=-1,0,+1$ and $a(t)$ is the scale factor.

  For $k=+1$, show that this metric can be written in the form

  $$d s^{2}=-d t^{2}+\gamma_{i j} d x^{i} d x^{j}=-d t^{2}+a^{2}(t)\left[d \chi^{2}+\sin ^{2} \chi\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  Calculate the equatorial circumference $(\theta=\pi / 2)$ of the submanifold defined by constant $t$ and $\chi$.

  Calculate the proper volume, defined by $\int \sqrt{\operatorname{det} \gamma} d^{3} x$, of the hypersurface defined by constant $t$.

  (b) The Friedmann equations are

  $$\begin{aligned} &3\left(\frac{\dot{a}^{2}+k}{a^{2}}\right)-\Lambda=8 \pi \rho, \\ &\frac{2 a \ddot{a}+\dot{a}^{2}+k}{a^{2}}-\Lambda=-8 \pi P, \end{aligned}$$

  where $\rho(t)$ is the energy density, $P(t)$ is the pressure, $\Lambda$ is the cosmological constant and dot denotes $d / d t$.

  The Einstein static universe has vanishing pressure, $P(t)=0$. Determine $a, k$ and $\Lambda$ as a function of the density $\rho$.

  The Einstein static universe with $a=a_{0}$ and $\rho=\rho_{0}$ is perturbed by radiation such that

  $$a=a_{0}+\delta a(t), \quad \rho=\rho_{0}+\delta \rho(t), \quad P=\frac{1}{3} \delta \rho(t)$$

  where $\delta a \ll a_{0}$ and $\delta \rho \ll \rho_{0}$. Show that the Einstein static universe is unstable to this perturbation.

  comment

Graph Theory

• Paper 2, Section II, H

  Graph Theory | Part II, 2017

  State and prove Hall's theorem about matchings in bipartite graphs.

  Let $A=\left(a_{i j}\right)$ be an $n \times n$ matrix, with all entries non-negative reals, such that every row sum and every column sum is 1. By applying Hall's theorem, show that there is a permutation $\sigma$ of $\{1, \ldots, n\}$ such that $a_{i \sigma(i)}>0$ for all $i$.

  comment

Integrable Systems

• Paper 2, Section II, A

  Integrable Systems | Part II, 2017

  Let $U$ and $V$ be non-singular $N \times N$ matrices depending on $(x, t, \lambda)$ which are periodic in $x$ with period $2 \pi$. Consider the associated linear problem

  $$\Psi_{x}=U \Psi, \quad \Psi_{t}=V \Psi$$

  for the vector $\Psi=\Psi(x, t ; \lambda)$. On the assumption that these equations are compatible, derive the zero curvature equation for $(U, V)$.

  Let $W=W(x, t, \lambda)$ denote the $N \times N$ matrix satisfying

  $$W_{x}=U W, \quad W(0, t, \lambda)=I_{N}$$

  where $I_{N}$ is the $N \times N$ identity matrix. You should assume $W$ is unique. By considering $\left(W_{t}-V W\right)_{x}$, show that the matrix $w(t, \lambda)=W(2 \pi, t, \lambda)$ satisfies the Lax equation

  $$w_{t}=[v, w], \quad v(t, \lambda) \equiv V(2 \pi, t, \lambda)$$

  Deduce that $\left\{\operatorname{tr}\left(w^{k}\right)\right\}_{k \geqslant 1}$ are first integrals.

  By considering the matrices

  $$\frac{1}{2 \mathrm{i} \lambda}\left[\begin{array}{cc} \cos u & -\mathrm{i} \sin u \\ \mathrm{i} \sin u & -\cos u \end{array}\right], \quad \frac{\mathrm{i}}{2}\left[\begin{array}{cc} 2 \lambda & u_{x} \\ u_{x} & -2 \lambda \end{array}\right]$$

  show that the periodic Sine-Gordon equation $u_{x t}=\sin u$ has infinitely many first integrals. [You need not prove anything about independence.]

  comment

Linear Analysis

• Paper 2, Section II, F

  Linear Analysis | Part II, 2017

  (a) Let $X$ be a normed vector space and $Y \subset X$ a closed subspace with $Y \neq X$. Show that $Y$ is nowhere dense in $X$.

  (b) State any version of the Baire Category theorem.

  (c) Let $X$ be an infinite-dimensional Banach space. Show that $X$ cannot have a countable algebraic basis, i.e. there is no countable subset $\left(x_{k}\right)_{k \in \mathbb{N}} \subset X$ such that every $x \in X$ can be written as a finite linear combination of elements of $\left(x_{k}\right)$.

  comment

Logic and Set Theory

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2017

  Give the inductive and synthetic definitions of ordinal addition, and prove that they are equivalent.

  Which of the following are always true for ordinals $\alpha, \beta$ and $\gamma$ and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha+\beta=\beta+\alpha$

  (ii) $(\alpha+\beta) \gamma=\alpha \gamma+\beta \gamma$

  (iii) $\alpha(\beta+\gamma)=\alpha \beta+\alpha \gamma$

  (iv) If $\alpha \beta=\beta \alpha$ then $\alpha^{2} \beta^{2}=\beta^{2} \alpha^{2}$

  (v) If $\alpha^{2} \beta^{2}=\beta^{2} \alpha^{2}$ then $\alpha \beta=\beta \alpha$

  [In parts (iv) and (v) you may assume without proof that ordinal multiplication is associative.]

  comment

Mathematical Biology

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2017

  A bacterial nutrient uptake model is represented by the reaction system

  $$\begin{array}{rll} 2 S+E & \stackrel{k_{1}}{\longrightarrow} & C \\ C & \stackrel{k_{2}}{\longrightarrow} 2 S+E \\ C \stackrel{k_{3}}{\longrightarrow} & E+2 P \end{array}$$

  where the $k_{i}$ are rate constants. Let $s, e, c$ and $p$ represent the concentrations of $S, E, C$ and $P$ respectively. Initially $s=s_{0}, e=e_{0}, c=0$ and $p=0$. Write down the governing differential equation system for the concentrations.

  Either by using the differential equations or directly from the reaction system above, find two invariant quantities. Use these to simplify the system to

  $$\begin{aligned} \dot{s} &=-2 k_{1} s^{2}\left(e_{0}-c\right)+2 k_{2} c \\ \dot{c} &=k_{1} s^{2}\left(e_{0}-c\right)-\left(k_{2}+k_{3}\right) c . \end{aligned}$$

  By setting $u=s / s_{0}$ and $v=c / e_{0}$ and rescaling time, show that the system can be written as

  $$\begin{aligned} u^{\prime} &=-2 u^{2}(1-v)+2(\mu-\lambda) v \\ \epsilon v^{\prime} &=\quad u^{2}(1-v)-\mu v \end{aligned}$$

  where $\epsilon=e_{0} / s_{0}$ and $\mu$ and $\lambda$ should be given. Give the initial conditions for $u$ and $v$.

  [Hint: Note that $2 X$ is equivalent to $X+X$ in reaction systems.]

  comment

Number Fields

• Paper 2, Section II, 18H

  Number Fields | Part II, 2017

  (a) Let $L$ be a number field, $\mathcal{O}_{L}$ the ring of integers in $L, \mathcal{O}_{L}^{*}$ the units in $\mathcal{O}_{L}, r$ the number of real embeddings of $L$, and $s$ the number of pairs of complex embeddings of $L$.

  Define a group homomorphism $\mathcal{O}_{L}^{*} \rightarrow \mathbb{R}^{r+s-1}$ with finite kernel, and prove that the image is a discrete subgroup of $\mathbb{R}^{r+s-1}$.

  (b) Let $K=\mathbb{Q}(\sqrt{d})$ where $d>1$ is a square-free integer. What is the structure of the group of units of $K$ ? Show that if $d$ is divisible by a prime $p \equiv 3(\bmod 4)$ then every unit of $K$ has norm $+1$. Find an example of $K$ with a unit of norm $-1$.

  comment

Number Theory

• Paper 2, Section I, G

  Number Theory | Part II, 2017

  State and prove Legendre's formula for $\pi(x)$. Use it to compute $\pi(42)$.

  comment

Numerical Analysis

• Paper 2, Section II, A

  Numerical Analysis | Part II, 2017

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1]$, equipped with the zero Dirichlet boundary conditions on $\partial \Omega$, is discretized with the nine-point formula:

  $$\begin{aligned} \Gamma_{9}\left[u_{i, j}\right]:=&-\frac{10}{3} u_{i, j}+\frac{2}{3}\left(u_{i+1, j}+u_{i-1, j}+u_{i, j+1}+u_{i, j-1}\right) \\ &+\frac{1}{6}\left(u_{i+1, j+1}+u_{i+1, j-1}+u_{i-1, j+1}+u_{i-1, j-1}\right)=h^{2} f_{i, j} \end{aligned}$$

  where $1 \leqslant i, j \leqslant m, u_{i, j} \approx u(i h, j h)$, and $(i h, j h)$ are the grid points with $h=\frac{1}{m+1}$.

  (i) Find the order of the local truncation error $\eta_{i, j}$ of the approximation.

  (ii) Prove that the order of the truncation error is smaller if $f$ satisfies the Laplace equation $\nabla^{2} f=0$.

  (iii) Show that the modified nine-point scheme

  $$\begin{aligned} \Gamma_{9}\left[u_{i, j}\right] &=h^{2} f_{i, j}+\frac{1}{12} h^{2} \Gamma_{5}\left[f_{i, j}\right] \\ &:=h^{2} f_{i, j}+\frac{1}{12} h^{2}\left(f_{i+1, j}+f_{i-1, j}+f_{i, j+1}+f_{i, j-1}-4 f_{i, j}\right) \end{aligned}$$

  has a truncation error of the same order as in part (ii).

  (iv) Let $\left(u_{i, j}\right)_{i, j=1}^{m}$ be a solution to the $m^{2} \times m^{2}$ system of linear equations $A \mathbf{u}=\mathbf{b}$ arising from the modified nine-point scheme in part (iii). Further, let $u(x, y)$ be the exact solution and let $e_{i, j}:=u_{i, j}-u(i h, j h)$ be the error of approximation at grid points. Prove that there exists a constant $c$ such that

  $$\|\mathbf{e}\|_{2}:=\left[\sum_{i, j=1}^{m}\left|e_{i, j}\right|^{2}\right]^{1 / 2}<c h^{3}, \quad h \rightarrow 0$$

  [Hint: The nine-point discretization of $\nabla^{2} u$ can be written as

  $$\Gamma_{9}[u]=\left(\Gamma_{5}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u=\left(\Delta_{x}^{2}+\Delta_{y}^{2}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u$$

  where $\Gamma_{5}[u]=\left(\Delta_{x}^{2}+\Delta_{y}^{2}\right) u$ is the five-point discretization and

  $$\left.\begin{array}{l} \Delta_{x}^{2} u(x, y):=u(x-h, y)-2 u(x, y)+u(x+h, y) \\ \Delta_{y}^{2} u(x, y):=u(x, y-h)-2 u(x, y)+u(x, y+h) \end{array}\right]$$

  [Hint: The matrix A of the nine-point scheme is symmetric, with the eigenvalues

  $$\lambda_{k, \ell}=-4 \sin ^{2} \frac{k \pi h}{2}-4 \sin ^{2} \frac{\ell \pi h}{2}+\frac{8}{3} \sin ^{2} \frac{k \pi h}{2} \sin ^{2} \frac{\ell \pi h}{2}, \quad 1 \leqslant k, \ell \leqslant m$$

  comment

Optimization and Control

• Paper 2, Section II, K

  Optimization and Control | Part II, 2017

  During each of $N$ time periods a venture capitalist, Vicky, is presented with an investment opportunity for which the rate of return for that period is a random variable; the rates of return in successive periods are independent identically distributed random variables with distributions concentrated on $[-1, \infty)$. Thus, if $x_{n}$ is Vicky's capital at period $n$, then $x_{n+1}=\left(1-p_{n}\right) x_{n}+p_{n} x_{n}\left(1+R_{n}\right)$, where $p_{n} \in[0,1]$ is the proportion of her capital she chooses to invest at period $n$, and $R_{n}$ is the rate of return for period $n$. Vicky desires to maximize her expected yield over $N$ periods, where the yield is defined as $\left(\frac{x_{N}}{x_{0}}\right)^{\frac{1}{N}}-1$, and $x_{0}$ and $x_{N}$ are respectively her initial and final capital.

  (a) Express the problem of finding an optimal policy in a dynamic programming framework.

  (b) Show that in each time period, the optimal strategy can be expressed in terms of the quantity $p^{*}$ which solves the optimization problem $\max _{p} \mathbb{E}\left(1+p R_{1}\right)^{1 / N}$. Show that $p^{*}>0$ if $\mathbb{E} R_{1}>0$. [Do not calculate $p^{*}$ explicitly.]

  (c) Compare her optimal policy with the policy which maximizes her expected final capital $x_{N}$.

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  Let $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ be a set of Hermitian operators obeying

  $$\left[\sigma_{i}, \sigma_{j}\right]=2 i \epsilon_{i j k} \sigma_{k} \quad \text { and } \quad(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=1$$

  where $\mathbf{n}$ is any unit vector. Show that $(*)$ implies that

  $$(\mathbf{a} \cdot \boldsymbol{\sigma})(\mathbf{b} \cdot \boldsymbol{\sigma})=\mathbf{a} \cdot \mathbf{b}+i(\mathbf{a} \times \mathbf{b}) \cdot \boldsymbol{\sigma}$$

  for any vectors a and $\mathbf{b}$. Explain, with reference to the properties $(*)$, how $\boldsymbol{\sigma}$ can be related to the intrinsic angular momentum $\mathbf{S}$ for a particle of spin $\frac{1}{2}$.

  Show that the operators $P_{\pm}=\frac{1}{2}(1 \pm \mathbf{n} \cdot \boldsymbol{\sigma})$ are Hermitian and obey

  $$P_{\pm}^{2}=P_{\pm}, \quad P_{+} P_{-}=P_{-} P_{+}=0$$

  Show how $P_{\pm}$can be used to write any state $|\chi\rangle$ as a linear combination of eigenstates of $\mathbf{n} \cdot \boldsymbol{\sigma}$. Use this to deduce that if the system is in a normalised state $|\chi\rangle$ when $\mathbf{n} \cdot \boldsymbol{\sigma}$ is measured, then the results $\pm 1$ will be obtained with probabilities

  $$\| P_{\pm}|\chi\rangle \|^{2}=\frac{1}{2}(1 \pm\langle\chi|\mathbf{n} \cdot \boldsymbol{\sigma}| \chi\rangle)$$

  If $|\chi\rangle$ is a state corresponding to the system having spin up along a direction defined by a unit vector $\mathbf{m}$, show that a measurement will find the system to have spin up along $\mathbf{n}$ with probability $\frac{1}{2}(1+\mathbf{n} \cdot \mathbf{m})$.

  comment

Principles of Statistics

• Paper 2, Section II, $26 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  We consider the problem of estimating $\theta$ in the model $\{f(x, \theta): \theta \in(0, \infty)\}$, where

  $$f(x, \theta)=(1-\alpha)(x-\theta)^{-\alpha} 1\{x \in[\theta, \theta+1]\}$$

  Here $1\{A\}$ is the indicator of the set $A$, and $\alpha \in(0,1)$ is known. This estimation is based on a sample of $n$ i.i.d. $X_{1}, \ldots, X_{n}$, and we denote by $X_{(1)}<\ldots<X_{(n)}$ the ordered sample.

  (a) Compute the mean and the variance of $X_{1}$. Construct an unbiased estimator of $\theta$ taking the form $\tilde{\theta}_{n}=\bar{X}_{n}+c(\alpha)$, where $\bar{X}_{n}=n^{-1} \sum_{i=1}^{n} X_{i}$, specifying $c(\alpha)$.

  (b) Show that $\tilde{\theta}_{n}$ is consistent and find the limit in distribution of $\sqrt{n}\left(\tilde{\theta}_{n}-\theta\right)$. Justify your answer, citing theorems that you use.

  (c) Find the maximum likelihood estimator $\hat{\theta}_{n}$ of $\theta$. Compute $\mathbf{P}\left(\hat{\theta}_{n}-\theta>t\right)$ for all real $t$. Is $\hat{\theta}_{n}$ unbiased?

  (d) For $t>0$, show that $\mathbf{P}\left(n^{\beta}\left(\hat{\theta}_{n}-\theta\right)>t\right)$ has a limit in $(0,1)$ for some $\beta>0$. Give explicitly the value of $\beta$ and the limit. Why should one favour using $\hat{\theta}_{n}$ over $\tilde{\theta}_{n}$ ?

  comment

Probability and Measure

• Paper 2, Section II, J

  Probability and Measure | Part II, 2017

  (a) Give the definition of the Fourier transform $\widehat{f}$ of a function $f \in L^{1}\left(\mathbb{R}^{d}\right)$.

  (b) Explain what it means for Fourier inversion to hold.

  (c) Prove that Fourier inversion holds for $g_{t}(x)=(2 \pi t)^{-d / 2} e^{-\|x\|^{2} /(2 t)}$. Show all of the steps in your computation. Deduce that Fourier inversion holds for Gaussian convolutions, i.e. any function of the form $f * g_{t}$ where $t>0$ and $f \in L^{1}\left(\mathbb{R}^{d}\right)$.

  (d) Prove that any function $f$ for which Fourier inversion holds has a bounded, continuous version. In other words, there exists $g$ bounded and continuous such that $f(x)=g(x)$ for a.e. $x \in \mathbb{R}^{d}$.

  (e) Does Fourier inversion hold for $f=\mathbf{1}_{[0,1]}$ ?

  comment

Representation Theory

• Paper 2, Section II, G

  Representation Theory | Part II, 2017

  In this question you may assume the following result. Let $\chi$ be a character of a finite group $G$ and let $g \in G$. If $\chi(g)$ is a rational number, then $\chi(g)$ is an integer.

  (a) If $a$ and $b$ are positive integers, we denote their highest common factor by $(a, b)$. Let $g$ be an element of order $n$ in the finite group $G$. Suppose that $g$ is conjugate to $g^{i}$ for all $i$ with $1 \leqslant i \leqslant n$ and $(i, n)=1$. Prove that $\chi(g)$ is an integer for all characters $\chi$ of $G$.

  [You may use the following result without proof. Let $\omega$ be an $n$th root of unity. Then

  is an integer.]

  Deduce that all the character values of symmetric groups are integers.

  (b) Let $G$ be a group of odd order.

  Let $\chi$ be an irreducible character of $G$ with $\chi=\bar{\chi}$. Prove that

  $$\left\langle\chi, 1_{G}\right\rangle=\frac{1}{|G|}(\chi(1)+2 \alpha),$$

  where $\alpha$ is an algebraic integer. Deduce that $\chi=1_{G}$.

  $$\begin{aligned} & \sum_{1 \leqslant i \leqslant n,} \omega^{i} \\ & \begin{aligned}&1 \leqslant i \leqslant n \\&(i, n)=1\end{aligned} \end{aligned}$$

  comment

Riemann Surfaces

• Paper 2, Section II, F

  Riemann Surfaces | Part II, 2017

  Let $f$ be a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$. Let $P$ be a fundamental parallelogram whose boundary contains no zeros or poles of $f$. Show that the number of zeros of $f$ in $P$ is the same as the number of poles of $f$ in $P$, both counted with multiplicities.

  Suppose additionally that $f$ is even. Show that there exists a rational function $Q(z)$ such that $f=Q(\wp)$, where $\wp$ is the Weierstrass $\wp$-function.

  Suppose $f$ is a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$, and $F$ is a meromorphic antiderivative of $f$, so that $F^{\prime}=f$. Is it necessarily true that $F$ is an elliptic function? Justify your answer.

  [You may use standard properties of the Weierstrass $\wp$-function throughout.]

  comment

Statistical Modelling

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2017

  A statistician is interested in the power of a $t$-test with level $5 \%$ in linear regression; that is, the probability of rejecting the null hypothesis $\beta_{0}=0$ with this test under an alternative with $\beta_{0}>0$.

  (a) State the distribution of the least-squares estimator $\hat{\beta}_{0}$, and hence state the form of the $t$-test statistic used.

  (b) Prove that the power does not depend on the other coefficients $\beta_{j}$ for $j>0$.

  comment

Statistical Physics

• Paper 2, Section II, 34D

  Statistical Physics | Part II, 2017

  (a) The entropy of a thermodynamic ensemble is defined by the formula

  $$S=-k \sum_{n} p(n) \log p(n)$$

  where $k$ is the Boltzmann constant. Explain what is meant by $p(n)$ in this formula. Write down an expression for $p(n)$ in the grand canonical ensemble, defining any variables you need. Hence show that the entropy $S$ is related to the grand canonical partition function $\mathcal{Z}(T, \mu, V)$ by

  $$S=k\left[\frac{\partial}{\partial T}(T \log \mathcal{Z})\right]_{\mu, V}$$

  (b) Consider a gas of non-interacting fermions with single-particle energy levels $\epsilon_{i}$.

  (i) Show that the grand canonical partition function $\mathcal{Z}$ is given by

  $$\log \mathcal{Z}=\sum_{i} \log \left(1+e^{-\left(\epsilon_{i}-\mu\right) /(k T)}\right)$$

  (ii) Assume that the energy levels are continuous with density of states $g(\epsilon)=A V \epsilon^{a}$, where $A$ and $a$ are positive constants. Prove that

  $$\log \mathcal{Z}=V T^{b} f(\mu / T)$$

  and give expressions for the constant $b$ and the function $f$.

  (iii) The gas is isolated and undergoes a reversible adiabatic change. By considering the ratio $S / N$, prove that $\mu / T$ remains constant. Deduce that $V T^{c}$ and $p V^{d}$ remain constant in this process, where $c$ and $d$ are constants whose values you should determine.

  comment

Stochastic Financial Models

• Paper 2, Section II, $27 \mathrm{~J}$

  Stochastic Financial Models | Part II, 2017

  (a) What is a Brownian motion?

  (b) Let $\left(B_{t}, t \geqslant 0\right)$ be a Brownian motion. Show that the process $\tilde{B}_{t}:=\frac{1}{c} B_{c^{2} t}$, $c \in \mathbb{R} \backslash\{0\}$, is also a Brownian motion.

  (c) Let $Z:=\sup _{t \geqslant 0} B_{t}$. Show that $c Z \stackrel{(d)}{=} Z$ for all $c>0$ (i.e. $c Z$ and $Z$ have the same laws). Conclude that $Z \in\{0,+\infty\}$ a.s.

  (d) Show that $\mathbb{P}[Z=+\infty]=1$.

  comment

Topics in Analysis

• Paper 2, Section I, F

  Topics in Analysis | Part II, 2017

  Are the following statements true or false? Give reasons, quoting any theorems that you need.

  (i) There is a sequence of polynomials $P_{n}$ with $P_{n}(t) \rightarrow \sin t$ uniformly on $\mathbb{R}$ as $n \rightarrow \infty$.

  (ii) If $f: \mathbb{R} \rightarrow \mathbb{R}$ is continuous, then there is a sequence of polynomials $Q_{n}$ with $Q_{n}(t) \rightarrow f(t)$ for each $t \in \mathbb{R}$ as $n \rightarrow \infty$.

  (iii) If $g:[1, \infty) \rightarrow \mathbb{R}$ is continuous with $g(t) \rightarrow 0$ as $t \rightarrow \infty$, then there is a sequence of polynomials $R_{n}$ with $R_{n}(1 / t) \rightarrow g(t)$ uniformly on $[1, \infty)$ as $n \rightarrow \infty$.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2017

  State and prove Baire's category theorem for complete metric spaces. Give an example to show that it may fail if the metric space is not complete.

  Let $f_{n}:[0,1] \rightarrow \mathbb{R}$ be a sequence of continuous functions such that $f_{n}(x)$ converges for all $x \in[0,1]$. Show that if $\epsilon>0$ is fixed we can find an $N \geqslant 0$ and a non-empty open interval $J \subseteq[0,1]$ such that $\left|f_{n}(x)-f_{m}(x)\right| \leqslant \epsilon$ for all $x \in J$ and all $n, m \geqslant N$.

  Let $g:[0,1] \rightarrow \mathbb{R}$ be defined by

  $$g(x)= \begin{cases}1 & \text { if } x \text { is rational } \\ 0 & \text { if } x \text { is irrational. }\end{cases}$$

  Show that we cannot find continuous functions $g_{n}:[0,1] \rightarrow \mathbb{R}$ with $g_{n}(x) \rightarrow g(x)$ for each $x \in[0,1]$ as $n \rightarrow \infty .$

  Define a sequence of continuous functions $h_{n}:[0,1] \rightarrow \mathbb{R}$ and a discontinuous function $h:[0,1] \rightarrow \mathbb{R}$ with $h_{n}(x) \rightarrow h(x)$ for each $x \in[0,1]$ as $n \rightarrow \infty$.

  comment

Waves

• Paper 2, Section II, B

  Waves | Part II, 2017

  Show that, for a one-dimensional flow of a perfect gas (with $\gamma>1$ ) at constant entropy, the Riemann invariants $R_{\pm}=u \pm 2\left(c-c_{0}\right) /(\gamma-1)$ are constant along characteristics $d x / d t=u \pm c .$

  Define a simple wave. Show that in a right-propagating simple wave

  $$\frac{\partial u}{\partial t}+\left(c_{0}+\frac{1}{2}(\gamma+1) u\right) \frac{\partial u}{\partial x}=0$$

  In some circumstances, dissipative effects may be modelled by

  $$\frac{\partial u}{\partial t}+\left(c_{0}+\frac{1}{2}(\gamma+1) u\right) \frac{\partial u}{\partial x}=-\alpha u$$

  where $\alpha$ is a positive constant. Suppose also that $u$ is prescribed at $t=0$ for all $x$, say $u(x, 0)=u_{0}(x)$. Demonstrate that, unless a shock develops, a solution of the form

  $$u(x, t)=u_{0}(\xi) e^{-\alpha t}$$

  can be found, where, for each $x$ and $t, \xi$ is determined implicitly as the solution of the equation

  $$x-c_{0} t=\xi+\frac{\gamma+1}{2 \alpha}\left(1-e^{-\alpha t}\right) u_{0}(\xi)$$

  Deduce that, despite the presence of dissipative effects, a shock will still form at some $(x, t)$ unless $\alpha>\alpha_{c}$, where

  $$\alpha_{c}=\frac{1}{2}(\gamma+1) \max _{u_{0}^{\prime}<0}\left|u_{0}^{\prime}(\xi)\right|$$

  comment