Part II, 2017, Paper 1

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2017

  Let $k$ be an algebraically closed field.

  (a) Let $X$ and $Y$ be varieties defined over $k$. Given a function $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of varieties.

  (b) If $X$ is an affine variety, show that the coordinate ring $A(X)$ coincides with the ring of regular functions on $X$. [Hint: You may assume a form of the Hilbert Nullstellensatz.]

  (c) Now suppose $X$ and $Y$ are affine varieties. Show that if $X$ and $Y$ are isomorphic, then there is an isomorphism of $k$-algebras $A(X) \cong A(Y)$.

  (d) Show that $Z\left(x^{2}-y^{3}\right) \subseteq \mathbb{A}^{2}$ is not isomorphic to $\mathbb{A}^{1}$.

  comment

Algebraic Topology

• Paper 1, Section II, I

  Algebraic Topology | Part II, 2017

  Let $X$ be a topological space and let $x_{0}$ and $x_{1}$ be points of $X$.

  (a) Explain how a path $u:[0,1] \rightarrow X$ from $x_{0}$ to $x_{1}$ defines a map $u_{\sharp}: \pi_{1}\left(X, x_{0}\right) \rightarrow$ $\pi_{1}\left(X, x_{1}\right)$.

  (b) Prove that $u_{\sharp}$ is an isomorphism of groups.

  (c) Let $\alpha, \beta:\left(S^{1}, 1\right) \rightarrow\left(X, x_{0}\right)$ be based loops in $X$. Suppose that $\alpha, \beta$ are homotopic as unbased maps, i.e. the homotopy is not assumed to respect basepoints. Show that the corresponding elements of $\pi_{1}\left(X, x_{0}\right)$ are conjugate.

  (d) Take $X$ to be the 2-torus $S^{1} \times S^{1}$. If $\alpha, \beta$ are homotopic as unbased loops as in part (c), then exhibit a based homotopy between them. Interpret this fact algebraically.

  (e) Exhibit a pair of elements in the fundamental group of $S^{1} \vee S^{1}$ which are homotopic as unbased loops but not as based loops. Justify your answer.

  comment

Analysis of Functions

• Paper 1, Section II, $22 F$

  Analysis of Functions | Part II, 2017

  Consider a sequence $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$ of measurable functions converging pointwise to a function $f: \mathbb{R} \rightarrow \mathbb{R}$. The Lebesgue measure is denoted by $\lambda$.

  (a) Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Define for $k, n \geqslant 1$ the sets

  $$E_{n}^{(k)}:=\bigcap_{m \geqslant n}\left\{x \in A|| f_{m}(x)-f(x) \mid \leqslant \frac{1}{k}\right\}$$

  Prove that for any $k, n \geqslant 1$, one has $E_{n}^{(k)} \subset E_{n+1}^{(k)}$ and $E_{n}^{(k+1)} \subset E_{n}^{(k)}$. Prove that for any $k \geqslant 1, A=\cup_{n \geqslant 1} E_{n}^{(k)}$.

  (b) Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Prove that for any $\varepsilon>0$, there is a Borel set $A_{\varepsilon} \subset A$ for which $\lambda\left(A \backslash A_{\varepsilon}\right) \leqslant \varepsilon$ and such that $f_{n}$ converges to $f$ uniformly on $A_{\varepsilon}$ as $n \rightarrow+\infty$. Is the latter still true when $\lambda(A)=+\infty$ ?

  (c) Assume additionally that $f_{n} \in L^{p}(\mathbb{R})$ for some $p \in(1,+\infty]$, and there exists an $M \geqslant 0$ for which $\left\|f_{n}\right\|_{L^{p}(\mathbb{R})} \leqslant M$ for all $n \geqslant 1$. Prove that $f \in L^{p}(\mathbb{R})$.

  (d) Let $f_{n}$ and $f$ be as in part (c). Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Prove that $f_{n}, f$ are integrable on $A$ and $\int_{A} f_{n} d \lambda \rightarrow \int_{A} f d \lambda$ as $n \rightarrow \infty$. Deduce that $f_{n}$ converges weakly to $f$ in $L^{p}(\mathbb{R})$ when $p<+\infty$. Does the convergence have to be strong?

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  A one-dimensional lattice has $N$ sites with lattice spacing $a$. In the tight-binding approximation, the Hamiltonian describing a single electron is given by

  $$H=E_{0} \sum_{n}|n\rangle\langle n|-J \sum_{n}(|n\rangle\langle n+1|+| n+1\rangle\langle n|)$$

  where $|n\rangle$ is the normalised state of the electron localised on the $n^{\text {th }}$lattice site. Using periodic boundary conditions $|N+1\rangle \equiv|1\rangle$, solve for the spectrum of this Hamiltonian to derive the dispersion relation

  $$E(k)=E_{0}-2 J \cos (k a)$$

  Define the Brillouin zone. Determine the number of states in the Brillouin zone.

  Calculate the velocity $v$ and effective mass $m^{\star}$ of the particle. For which values of $k$ is the effective mass negative?

  In the semi-classical approximation, derive an expression for the time-dependence of the position of the electron in a constant electric field.

  Describe how the concepts of metals and insulators arise in the model above.

  comment

Applied Probability

• Paper 1, Section II, $27 \mathrm{~K}$

  Applied Probability | Part II, 2017

  (a) Define a continuous time Markov chain $X$ with infinitesimal generator $Q$ and jump chain $Y$.

  (b) Let $i$ be a transient state of a continuous-time Markov chain $X$ with $X(0)=i$. Show that the time spent in state $i$ has an exponential distribution and explicitly state its parameter.

  [You may use the fact that if $S \sim \operatorname{Exp}(\lambda)$, then $\mathbb{E}\left[e^{\theta S}\right]=\lambda /(\lambda-\theta)$ for $\theta<\lambda$.]

  (c) Let $X$ be an asymmetric random walk in continuous time on the non-negative integers with reflection at 0 , so that

  $$q_{i, j}= \begin{cases}\lambda & \text { if } \quad j=i+1, i \geqslant 0 \\ \mu & \text { if } \quad j=i-1, i \geqslant 1\end{cases}$$

  Suppose that $X(0)=0$ and $\lambda>\mu$. Show that for all $r \geqslant 1$, the total time $T_{r}$ spent in state $r$ is exponentially distributed with parameter $\lambda-\mu$.

  Assume now that $X(0)$ has some general distribution with probability generating function $G$. Find the expected amount of time spent at 0 in terms of $G$.

  comment

Automata and Formal Languages

• Paper 1, Section I, $4 \mathrm{H}$

  Automata and Formal Languages | Part II, 2017

  (a) Prove that every regular language is also a context-free language (CFL).

  (b) Show that, for any fixed $n>0$, the set of regular expressions over the alphabet $\left\{a_{1}, \ldots, a_{n}\right\}$ is a CFL, but not a regular language.

  comment

• Paper 1, Section II, $11 H$

  Automata and Formal Languages | Part II, 2017

  (a) Give an encoding to integers of all deterministic finite-state automata (DFAs). [Here the alphabet of each such DFA is always taken from the set $\{0,1, \ldots\}$, and the states for each such DFA are always taken from the set $\left.\left\{q_{0}, q_{1}, \ldots\right\} .\right]$

  (b) Show that the set of codes for which the corresponding DFA $D_{n}$ accepts a finite language is recursive. Moreover, if the language $\mathcal{L}\left(D_{n}\right)$ is finite, show that we can compute its size $\left|\mathcal{L}\left(D_{n}\right)\right|$ from $n$.

  comment

Classical Dynamics

• Paper 1, Section I, E

  Classical Dynamics | Part II, 2017

  Consider a Lagrangian system with Lagrangian $L\left(x_{A}, \dot{x}_{A}, t\right)$, where $A=1, \ldots, 3 N$, and constraints

  $$f_{\alpha}\left(x_{A}, t\right)=0, \quad \alpha=1, \ldots, 3 N-n .$$

  Use the method of Lagrange multipliers to show that this is equivalent to a system with Lagrangian $\mathcal{L}\left(q_{i}, \dot{q}_{i}, t\right) \equiv L\left(x_{A}\left(q_{i}, t\right), \dot{x}_{A}\left(q_{i}, \dot{q}_{i}, t\right), t\right)$, where $i=1, \ldots, n$, and $q_{i}$ are coordinates on the surface of constraints.

  Consider a bead of unit mass in $\mathbb{R}^{2}$ constrained to move (with no potential) on a wire given by an equation $y=f(x)$, where $(x, y)$ are Cartesian coordinates. Show that the Euler-Lagrange equations take the form

  $$\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial \dot{x}}=\frac{\partial \mathcal{L}}{\partial x}$$

  for some $\mathcal{L}=\mathcal{L}(x, \dot{x})$ which should be specified. Find one first integral of the EulerLagrange equations, and thus show that

  $$t=F(x)$$

  where $F(x)$ should be given in the form of an integral.

  [Hint: You may assume that the Euler-Lagrange equations hold in all coordinate systems.]

  comment

Coding and Cryptography

• Paper 1, Section I, G

  Coding and Cryptography | Part II, 2017

  Let $C$ be a binary code of length $n$. Define the following decoding rules: (i) ideal observer, (ii) maximum likelihood, (iii) minimum distance.

  Let $p$ denote the probability that a digit is mistransmitted and suppose $p<1 / 2$. Prove that maximum likelihood and minimum distance decoding agree.

  Suppose codewords 000 and 111 are sent with probabilities $4 / 5$ and $1 / 5$ respectively with error probability $p=1 / 4$. If we receive 110 , how should it be decoded according to the three decoding rules above?

  comment

• Paper 1, Section II, G

  Coding and Cryptography | Part II, 2017

  Let $C$ be a binary linear code. Explain what it means for $C$ to have length $n$ and $\operatorname{rank} k$. Explain what it means for a codeword of $C$ to have weight $j$.

  Suppose $C$ has length $n$, rank $k$, and $A_{j}$ codewords of weight $j$. The weight enumerator polynomial of $C$ is given by

  $$W_{C}(s, t)=\sum_{j=0}^{n} A_{j} s^{j} t^{n-j}$$

  What is $W_{C}(1,1) ?$ Prove that $W_{C}(s, t)=W_{C}(t, s)$ if and only if $W_{C}(1,0)=1$.

  Define the dual code $C^{\perp}$ of $C$.

  (i) Let $\mathbf{y} \in \mathbb{F}_{2}^{n}$. Show that

  $$\sum_{\mathbf{x} \in C}(-1)^{\mathbf{x} \cdot \mathbf{y}}= \begin{cases}2^{k}, & \text { if } \mathbf{y} \in C^{\perp} \\ 0, & \text { otherwise }\end{cases}$$

  (ii) Extend the definition of weight to give a weight $w(\mathbf{y})$ for $\mathbf{y} \in \mathbb{F}_{2}^{n}$. Suppose that for $t$ real and all $\mathbf{x} \in C$

  $$\sum_{\mathbf{y} \in \mathbb{F}_{2}^{n}} t^{w(\mathbf{y})}(-1)^{\mathbf{x} \cdot \mathbf{y}}=(1-t)^{w(\mathbf{x})}(1+t)^{n-w(\mathbf{x})}$$

  For $s$ real, by evaluating

  $$\sum_{\mathbf{x} \in C}\left(\sum_{\mathbf{y} \in \mathbb{F}_{2}^{n}}(-1)^{\mathbf{x} \cdot \mathbf{y}}\left(\frac{s}{t}\right)^{w(\mathbf{y})}\right)$$

  in two different ways, show that

  $$W_{C^{\perp}}(s, t)=2^{-k} W_{C}(t-s, t+s) .$$

  comment

Cosmology

• Paper 1, Section I, C

  Cosmology | Part II, 2017

  In a homogeneous and isotropic universe, describe the relative displacement $\mathbf{r}(t)$ of two galaxies in terms of a scale factor $a(t)$. Show how the relative velocity $\mathbf{v}(t)$ of these galaxies is given by the relation $\mathbf{v}(t)=H(t) \mathbf{r}(t)$, where you should specify $H(t)$ in terms of $a(t)$.

  From special relativity, the Doppler shift of light emitted by a particle moving away radially with speed $v$ can be approximated by

  $$\frac{\lambda_{0}}{\lambda_{\mathrm{e}}}=\sqrt{\frac{1+v / c}{1-v / c}}=1+\frac{v}{c}+\mathcal{O}\left(\frac{v^{2}}{c^{2}}\right)$$

  where $\lambda_{e}$ is the wavelength of emitted light and $\lambda_{0}$ is the observed wavelength. For the observed light from distant galaxies in a homogeneous and isotropic expanding universe, show that the redshift defined by $1+z \equiv \lambda_{0} / \lambda_{\mathrm{e}}$ is given by

  $$1+z=\frac{a\left(t_{0}\right)}{a\left(t_{\mathrm{e}}\right)}$$

  where $t_{\mathrm{e}}$ is the time of emission and $t_{0}$ is the observation time.

  comment

• Paper 1, Section II, C

  Cosmology | Part II, 2017

  The evolution of a flat $(k=0)$ homogeneous and isotropic universe with scale factor $a(t)$, mass density $\rho(t)$ and pressure $P(t)$ obeys the Friedmann and energy conservation equations

  $$\begin{array}{r} H^{2}(t)=\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho+\frac{\Lambda c^{2}}{3} \\ \dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+P / c^{2}\right) \end{array}$$

  where $H(t)$ is the Hubble parameter (observed today $t=t_{0}$ with value $H_{0}=H\left(t_{0}\right)$ ) and $\Lambda>0$ is the cosmological constant.

  Use these two equations to derive the acceleration equation

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)+\frac{\Lambda c^{2}}{3}$$

  For pressure-free matter $\left(\rho=\rho_{\mathrm{M}}\right.$ and $\left.P_{\mathrm{M}}=0\right)$, solve the energy conservation equation to show that the Friedmann and acceleration equations can be re-expressed as

  $$\begin{gathered} H=H_{0} \sqrt{\frac{\Omega_{\mathrm{M}}}{a^{3}}+\Omega_{\Lambda}} \\ \frac{\ddot{a}}{a}=-\frac{H_{0}^{2}}{2}\left[\frac{\Omega_{\mathrm{M}}}{a^{3}}-2 \Omega_{\Lambda}\right] \end{gathered}$$

  where we have taken $a\left(t_{0}\right)=1$ and we have defined the relative densities today $\left(t=t_{0}\right)$ as

  $$\Omega_{\mathrm{M}}=\frac{8 \pi G}{3 H_{0}^{2}} \rho_{\mathrm{M}}\left(t_{0}\right) \quad \text { and } \quad \Omega_{\Lambda}=\frac{\Lambda c^{2}}{3 H_{0}^{2}}$$

  Solve the Friedmann equation and show that the scale factor can be expressed as

  $$a(t)=\left(\frac{\Omega_{\mathrm{M}}}{\Omega_{\Lambda}}\right)^{1 / 3} \sinh ^{2 / 3}\left(\frac{3}{2} \sqrt{\Omega_{\Lambda}} H_{0} t\right)$$

  Find an expression for the time $\bar{t}$ at which the matter density $\rho_{\mathrm{M}}$ and the effective density caused by the cosmological constant $\Lambda$ are equal. (You need not evaluate this explicitly.)

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2017

  Define what it means for a subset $X \subset \mathbb{R}^{N}$ to be a manifold.

  For manifolds $X$ and $Y$, state what it means for a map $f: X \rightarrow Y$ to be smooth. For such a smooth map, and $x \in X$, define the differential map $d f_{x}$.

  What does it mean for $y \in Y$ to be a regular value of $f$ ? Give an example of a map $f: X \rightarrow Y$ and a $y \in Y$ which is not a regular value of $f$.

  Show that the set $S L_{n}(\mathbb{R})$ of $n \times n$ real-valued matrices with determinant 1 can naturally be viewed as a manifold $S L_{n}(\mathbb{R}) \subset \mathbb{R}^{n^{2}}$. What is its dimension? Show that matrix multiplication $f: S L_{n}(\mathbb{R}) \times S L_{n}(\mathbb{R}) \rightarrow S L_{n}(\mathbb{R})$, defined by $f(A, B)=A B$, is smooth. [Standard theorems may be used without proof if carefully stated.] Describe the tangent space of $S L_{n}(\mathbb{R})$ at the identity $I \in S L_{n}(\mathbb{R})$ as a subspace of $\mathbb{R}^{n^{2}}$.

  Show that if $n \geqslant 2$ then the set of real-valued matrices with determinant 0 , viewed as a subset of $\mathbb{R}^{n^{2}}$, is not a manifold.

  comment

Dynamical Systems

• Paper 1, Section II, A

  Dynamical Systems | Part II, 2017

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=-x+x^{3}+\beta x y^{2} \\ &\dot{y}=-y+\beta x^{2} y+y^{3} \end{aligned}$$

  where $\beta>-1$ is a constant.

  (a) Find the fixed points of the system, and classify them for $\beta \neq 1$.

  Sketch the phase plane for each of the cases (i) $\beta=\frac{1}{2}$ (ii) $\beta=2$ and (iii) $\beta=1$.

  (b) Given $\beta>2$, show that the domain of stability of the origin includes the union over $k \in \mathbb{R}$ of the regions

  $$x^{2}+k^{2} y^{2}<\frac{4 k^{2}\left(1+k^{2}\right)(\beta-1)}{\beta^{2}\left(1+k^{2}\right)^{2}-4 k^{2}} .$$

  By considering $k \gg 1$, or otherwise, show that more information is obtained from the union over $k$ than considering only the case $k=1$.

  $\left[\right.$ Hint: If $B>A, C$ then $\left.\max _{u \in[0,1]}\left\{A u^{2}+2 B u(1-u)+C(1-u)^{2}\right\}=\frac{B^{2}-A C}{2 B-A-C} \cdot\right]$

  comment

Electrodynamics

• Paper 1, Section II, 35D

  Electrodynamics | Part II, 2017

  In some inertial reference frame $S$, there is a uniform electric field $\mathbf{E}$ directed along the positive $y$-direction and a uniform magnetic field $\mathbf{B}$ directed along the positive $z$ direction. The magnitudes of the fields are $E$ and $B$, respectively, with $E<c B$. Show that it is possible to find a reference frame in which the electric field vanishes, and determine the relative speed $\beta c$ of the two frames and the magnitude of the magnetic field in the new frame.

  [Hint: You may assume that under a standard Lorentz boost with speed $v=\beta$ c along the $x$-direction, the electric and magnetic field components transform as

  $$\left(\begin{array}{c} E_{x}^{\prime} \\ E_{y}^{\prime} \\ E_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} E_{x} \\ \gamma(\beta)\left(E_{y}-v B_{z}\right) \\ \gamma(\beta)\left(E_{z}+v B_{y}\right) \end{array}\right) \quad a n d \quad\left(\begin{array}{c} B_{x}^{\prime} \\ B_{y}^{\prime} \\ B_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} B_{x} \\ \gamma(\beta)\left(B_{y}+v E_{z} / c^{2}\right) \\ \gamma(\beta)\left(B_{z}-v E_{y} / c^{2}\right) \end{array}\right),$$

  where the Lorentz factor $\gamma(\beta)=\left(1-\beta^{2}\right)^{-1 / 2}$.]

  A point particle of mass $m$ and charge $q$ moves relativistically under the influence of the fields $\mathbf{E}$ and $\mathbf{B}$. The motion is in the plane $z=0$. By considering the motion in the reference frame in which the electric field vanishes, or otherwise, show that, with a suitable choice of origin, the worldline of the particle has components in the frame $S$ of the form

  $$\begin{aligned} &c t(\tau)=\gamma(u / c) \gamma(\beta)\left[c \tau+\frac{\beta u}{\omega} \sin \omega \tau\right] \\ &x(\tau)=\gamma(u / c) \gamma(\beta)\left[\beta c \tau+\frac{u}{\omega} \sin \omega \tau\right] \\ &y(\tau)=\frac{u \gamma(u / c)}{\omega} \cos \omega \tau \end{aligned}$$

  Here, $u$ is a constant speed with Lorentz factor $\gamma(u / c), \tau$ is the particle's proper time, and $\omega$ is a frequency that you should determine.

  Using dimensionless coordinates,

  $$\tilde{x}=\frac{\omega}{u \gamma(u / c)} x \quad \text { and } \quad \tilde{y}=\frac{\omega}{u \gamma(u / c)} y$$

  sketch the trajectory of the particle in the $(\tilde{x}, \tilde{y})$-plane in the limiting cases $2 \pi \beta \ll u / c$ and $2 \pi \beta \gg u / c$.

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2017

  Fluid of density $\rho$ and dynamic viscosity $\mu$ occupies the region $y>0$ in Cartesian coordinates $(x, y, z)$. A semi-infinite, dense array of cilia occupy the half plane $y=0$, $x>0$ and apply a stress in the $x$-direction on the adjacent fluid, working at a constant and uniform rate $\rho P$ per unit area, which causes the fluid to move with steady velocity $\mathbf{u}=(u(x, y), v(x, y), 0)$. Give a careful physical explanation of the boundary condition

  $$\left.u \frac{\partial u}{\partial y}\right|_{y=0}=-\frac{P}{\nu} \quad \text { for } \quad x>0$$

  paying particular attention to signs, where $\nu$ is the kinematic viscosity of the fluid. Why would you expect the fluid motion to be confined to a thin region near $y=0$ for sufficiently large values of $x$ ?

  Write down the viscous-boundary-layer equations governing the thin region of fluid motion. Show that the flow can be approximated by a stream function

  $$\psi(x, y)=U(x) \delta(x) f(\eta), \quad \text { where } \quad \eta=\frac{y}{\delta(x)}$$

  Determine the functions $U(x)$ and $\delta(x)$. Show that the dimensionless function $f(\eta)$ satisfies

  $$f^{\prime \prime \prime}=\frac{1}{5} f^{\prime 2}-\frac{3}{5} f f^{\prime \prime}$$

  What boundary conditions must be satisfied by $f(\eta)$ ? By considering how the volume flux varies with downstream location $x$, or otherwise, determine (with justification) the sign of the transverse flow $v$.

  comment

Further Complex Methods

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2017

  Calculate the value of the integral

  $$P \int_{-\infty}^{\infty} \frac{e^{-i x}}{x^{n}} d x$$

  where $P$ stands for Principal Value and $n$ is a positive integer.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2017

  The Riemann zeta function is defined by

  $$\zeta_{R}(s)=\sum_{n=1}^{\infty} n^{-s}$$

  for $\operatorname{Re}(s)>1$.

  Show that

  $$\zeta_{R}(s)=\frac{1}{\Gamma(s)} \int_{0}^{\infty} \frac{t^{s-1}}{e^{t}-1} d t$$

  Let $I(s)$ be defined by

  $$I(s)=\frac{\Gamma(1-s)}{2 \pi i} \int_{C} \frac{t^{s-1}}{e^{-t}-1} d t$$

  where $C$ is the Hankel contour.

  Show that $I(s)$ provides an analytic continuation of $\zeta_{R}(s)$ for a range of $s$ which should be determined.

  Hence evaluate $\zeta_{R}(-1)$.

  comment

Galois Theory

• Paper 1, Section II, I

  Galois Theory | Part II, 2017

  (a) Let $K$ be a field and let $f(t) \in K[t]$. What does it mean for a field extension $L$ of $K$ to be a splitting field for $f(t)$ over $K$ ?

  Show that the splitting field for $f(t)$ over $K$ is unique up to isomorphism.

  (b) Find the Galois groups over the rationals $\mathbb{Q}$ for the following polynomials: (i) $t^{4}+2 t+2$. (ii) $t^{5}-t-1$.

  comment

General Relativity

• Paper 1, Section II, D

  General Relativity | Part II, 2017

  A static black hole in a five-dimensional spacetime is described by the metric

  $$d s^{2}=-\left(1-\frac{\mu}{r^{2}}\right) d t^{2}+\left(1-\frac{\mu}{r^{2}}\right)^{-1} d r^{2}+r^{2}\left[d \psi^{2}+\sin ^{2} \psi\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  where $\mu>0$ is a constant.

  A geodesic lies in the plane $\theta=\psi=\pi / 2$ and has affine parameter $\lambda$. Show that

  $$E=\left(1-\frac{\mu}{r^{2}}\right) \frac{d t}{d \lambda} \quad \text { and } \quad L=r^{2} \frac{d \phi}{d \lambda}$$

  are both constants of motion. Write down a third constant of motion.

  Show that timelike and null geodesics satisfy the equation

  $$\frac{1}{2}\left(\frac{d r}{d \lambda}\right)^{2}+V(r)=\frac{1}{2} E^{2}$$

  for some potential $V(r)$ which you should determine.

  Circular geodesics satisfy the equation $V^{\prime}(r)=0$. Calculate the values of $r$ for which circular null geodesics exist and for which circular timelike geodesics exist. Which are stable and which are unstable? Briefly describe how this compares to circular geodesics in the four-dimensional Schwarzschild geometry.

  comment

Graph Theory

• Paper 1, Section II, H

  Graph Theory | Part II, 2017

  Let $G$ be a graph of order $n \geqslant 3$ satisfying $\delta(G) \geqslant \frac{n}{2}$. Show that $G$ is Hamiltonian.

  Give an example of a planar graph $G$, with $\chi(G)=4$, that is Hamiltonian, and also an example of a planar graph $G$, with $\chi(G)=4$, that is not Hamiltonian.

  Let $G$ be a planar graph with the property that the boundary of the unbounded face is a Hamilton cycle of $G$. Prove that $\chi(G) \leqslant 3$.

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2017

  Define a Lie point symmetry of the first order ordinary differential equation $\Delta[t, \mathbf{x}, \dot{\mathbf{x}}]=$ 0. Describe such a Lie point symmetry in terms of the vector field that generates it.

  Consider the $2 n$-dimensional Hamiltonian system $(M, H)$ governed by the differential equation

  $$\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} t}=J \frac{\partial H}{\partial \mathbf{x}}$$

  Define the Poisson bracket $\{\cdot, \cdot\}$. For smooth functions $f, g: M \rightarrow \mathbf{R}$ show that the associated Hamiltonian vector fields $V_{f}, V_{g}$ satisfy

  $$\left[V_{f}, V_{g}\right]=-V_{\{f, g\}} .$$

  If $F: M \rightarrow \mathbf{R}$ is a first integral of $(M, H)$, show that the Hamiltonian vector field $V_{F}$ generates a Lie point symmetry of $(\star)$. Prove the converse is also true if $(\star)$ has a fixed point, i.e. a solution of the form $\mathbf{x}(t)=\mathbf{x}_{0}$.

  comment

Linear Analysis

• Paper 1, Section II, F

  Linear Analysis | Part II, 2017

  Let $X$ be a normed vector space over the real numbers.

  (a) Define the dual space $X^{*}$ of $X$ and prove that $X^{*}$ is a Banach space. [You may use without proof that $X^{*}$ is a vector space.]

  (b) The Hahn-Banach theorem states the following. Let $X$ be a real vector space, and let $p: X \rightarrow \mathbb{R}$ be sublinear, i.e., $p(x+y) \leqslant p(x)+p(y)$ and $p(\lambda x)=\lambda p(x)$ for all $x, y \in X$ and all $\lambda>0$. Let $Y \subset X$ be a linear subspace, and let $g: Y \rightarrow \mathbb{R}$ be linear and satisfy $g(y) \leqslant p(y)$ for all $y \in Y$. Then there exists a linear functional $f: X \rightarrow \mathbb{R}$ such that $f(x) \leqslant p(x)$ for all $x \in X$ and $\left.f\right|_{Y}=g$.

  Using the Hahn-Banach theorem, prove that for any non-zero $x_{0} \in X$ there exists $f \in X^{*}$ such that $f\left(x_{0}\right)=\left\|x_{0}\right\|$ and $\|f\|=1$.

  (c) Show that $X$ can be embedded isometrically into a Banach space, i.e. find a Banach space $Y$ and a linear map $\Phi: X \rightarrow Y$ with $\|\Phi(x)\|=\|x\|$ for all $x \in X$.

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2017

  State the Completeness Theorem for Propositional Logic.

  [You do not need to give definitions of the various terms involved.]

  State the Compactness Theorem and the Decidability Theorem, and deduce them from the Completeness Theorem.

  A set $S$ of propositions is called finitary if there exists a finite set $T$ of propositions such that $\{t: S \vdash t\}=\{t: T \vdash t\}$. Give examples to show that an infinite set of propositions may or may not be finitary.

  Now let $A$ and $B$ be sets of propositions such that every valuation is a model of exactly one of $A$ and $B$. Show that there exist finite subsets $A^{\prime}$ of $A$ and $B^{\prime}$ of $B$ with $A^{\prime} \cup B^{\prime} \models \perp$, and deduce that $A$ and $B$ are finitary.

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2017

  A model of insect dispersal and growth in one spatial dimension is given by

  $$\frac{\partial N}{\partial t}=D \frac{\partial}{\partial x}\left(N^{2} \frac{\partial N}{\partial x}\right)+\alpha N, \quad N(x, 0)=N_{0} \delta(x),$$

  where $\alpha, D$ and $N_{0}$ are constants, $D>0$, and $\alpha$ may be positive or negative.

  By setting $N(x, t)=R(x, \tau) e^{\alpha t}$, where $\tau(t)$ is some time-like variable satisfying $\tau(0)=0$, show that a suitable choice of $\tau$ yields

  $$R_{\tau}=\left(R^{2} R_{x}\right)_{x}, \quad R(x, 0)=N_{0} \delta(x)$$

  where subscript denotes differentiation with respect to $x$ or $\tau$.

  Consider a similarity solution of the form $R(x, \tau)=F(\xi) / \tau^{\frac{1}{4}}$ where $\xi=x / \tau^{\frac{1}{4}}$. Show that $F$ must satisfy

  $$-\frac{1}{4}(F \xi)^{\prime}=\left(F^{2} F^{\prime}\right)^{\prime} \quad \text { and } \quad \int_{-\infty}^{+\infty} F(\xi) d \xi=N_{0}$$

  [You may use the fact that these are solved by

  $$F(\xi)= \begin{cases}\frac{1}{2} \sqrt{\xi_{0}^{2}-\xi^{2}} & \text { for }|\xi|<\xi_{0} \\ 0 & \text { otherwise }\end{cases}$$

  where $\left.\xi_{0}=\sqrt{4 N_{0} / \pi} .\right]$

  For $\alpha<0$, what is the maximum distance from the origin that insects ever reach? Give your answer in terms of $D, \alpha$ and $N_{0}$.

  comment

Number Fields

• Paper 1, Section II, H

  Number Fields | Part II, 2017

  Let $\mathcal{O}_{L}$ be the ring of integers in a number field $L$, and let $\mathfrak{a} \leqslant \mathcal{O}_{L}$ be a non-zero ideal of $\mathcal{O}_{L}$.

  (a) Show that $\mathfrak{a} \cap \mathbb{Z} \neq\{0\}$.

  (b) Show that $\mathcal{O}_{L} / \mathfrak{a}$ is a finite abelian group.

  (c) Show that if $x \in L$ has $x \mathfrak{a} \subseteq \mathfrak{a}$, then $x \in \mathcal{O}_{L}$.

  (d) Suppose $[L: \mathbb{Q}]=2$, and $\mathfrak{a}=\langle b, \alpha\rangle$, with $b \in \mathbb{Z}$ and $\alpha \in \mathcal{O}_{L}$. Show that $\langle b, \alpha\rangle\langle b, \bar{\alpha}\rangle$ is principal.

  [You may assume that $\mathfrak{a}$ has an integral basis.]

  comment

Number Theory

• Paper 1, Section $I$, G

  Number Theory | Part II, 2017

  Define the Legendre symbol $\left(\frac{a}{p}\right)$.

  State Gauss' lemma and use it to compute $\left(\frac{2}{p}\right)$ where $p$ is an odd prime.

  Show that if $m \geqslant 4$ is a power of 2 , and $p$ is a prime dividing $2^{m}+1$, then $p \equiv 1(\bmod 4 m)$.

  comment

Numerical Analysis

• Paper 1, Section II, A

  Numerical Analysis | Part II, 2017

  State the Householder-John theorem and explain how it can be used in designing iterative methods for solving a system of linear equations $A \mathbf{x}=\mathbf{b}$. [You may quote other relevant theorems if needed.]

  Consider the following iterative scheme for solving $A \mathbf{x}=\mathbf{b}$. Let $A=L+D+U$, where $D$ is the diagonal part of $A$, and $L$ and $U$ are the strictly lower and upper triangular parts of $A$, respectively. Then, with some starting vector $\mathbf{x}^{(0)}$, the scheme is as follows:

  $$(D+\omega L) \mathbf{x}^{(k+1)}=[(1-\omega) D-\omega U] \mathbf{x}^{(k)}+\omega \mathbf{b} .$$

  Prove that if $A$ is a symmetric positive definite matrix and $\omega \in(0,2)$, then, for any $\mathbf{x}^{(0)}$, the above iteration converges to the solution of the system $A \mathbf{x}=\mathbf{b}$.

  Which method corresponds to the case $\omega=1 ?$

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  The position and momentum operators of the harmonic oscillator can be written as

  $$\hat{x}=\left(\frac{\hbar}{2 m \omega}\right)^{1 / 2}\left(a+a^{\dagger}\right), \quad \hat{p}=\left(\frac{\hbar m \omega}{2}\right)^{1 / 2} i\left(a^{\dagger}-a\right)$$

  where $m$ is the mass, $\omega$ is the frequency and the Hamiltonian is

  $$H=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2}$$

  Assuming that

  $$[\hat{x}, \hat{p}]=i \hbar$$

  derive the commutation relations for $a$ and $a^{\dagger}$. Construct the Hamiltonian in terms of $a$ and $a^{\dagger}$. Assuming that there is a unique ground state, explain how all other energy eigenstates can be constructed from it. Determine the energy of each of these eigenstates.

  Consider the modified Hamiltonian

  $$H^{\prime}=H+\lambda \hbar \omega\left(a^{2}+a^{\dagger 2}\right)$$

  where $\lambda$ is a dimensionless parameter. Use perturbation theory to calculate the modified energy levels to second order in $\lambda$, quoting any standard formulae that you require. Show that the modified Hamiltonian can be written as

  $$H^{\prime}=\frac{1}{2 m}(1-2 \lambda) \hat{p}^{2}+\frac{1}{2} m \omega^{2}(1+2 \lambda) \hat{x}^{2} .$$

  Assuming $|\lambda|<\frac{1}{2}$, calculate the modified energies exactly. Show that the results are compatible with those obtained from perturbation theory.

  comment

Principles of Statistics

• Paper 1, Section II, $28 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  For a positive integer $n$, we want to estimate the parameter $p$ in the binomial statistical model $\{\operatorname{Bin}(n, p), p \in[0,1]\}$, based on an observation $X \sim \operatorname{Bin}(n, p)$.

  (a) Compute the maximum likelihood estimator for $p$. Show that the posterior distribution for $p$ under a uniform prior on $[0,1]$ is $\operatorname{Beta}(a, b)$, and specify $a$ and $b$. [The p.d.f. of $\operatorname{Beta}(a, b)$ is given by

  $$\left.f_{a, b}(p)=\frac{(a+b-1) !}{(a-1) !(b-1) !} p^{a-1}(1-p)^{b-1} .\right]$$

  (b) (i) For a risk function $L$, define the risk of an estimator $\hat{p}$ of $p$, and the Bayes risk under a prior $\pi$ for $p$.

  (ii) Under the loss function

  $$L(\hat{p}, p)=\frac{(\hat{p}-p)^{2}}{p(1-p)}$$

  find a Bayes optimal estimator for the uniform prior. Give its risk as a function of $p$.

  (iii) Give a minimax optimal estimator for the loss function $L$ given above. Justify your answer.

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2017

  (a) Give the definition of the Borel $\sigma$-algebra on $\mathbb{R}$ and a Borel function $f: E \rightarrow \mathbb{R}$ where $(E, \mathcal{E})$ is a measurable space.

  (b) Suppose that $\left(f_{n}\right)$ is a sequence of Borel functions which converges pointwise to a function $f$. Prove that $f$ is a Borel function.

  (c) Let $R_{n}:[0,1) \rightarrow \mathbb{R}$ be the function which gives the $n$th binary digit of a number in $[0,1$ ) (where we do not allow for the possibility of an infinite sequence of 1 s). Prove that $R_{n}$ is a Borel function.

  (d) Let $f:[0,1)^{2} \rightarrow[0, \infty]$ be the function such that $f(x, y)$ for $x, y \in[0,1)^{2}$ is equal to the number of digits in the binary expansions of $x, y$ which disagree. Prove that $f$ is non-negative measurable.

  (e) Compute the Lebesgue measure of $f^{-1}([0, \infty))$, i.e. the set of pairs of numbers in $[0,1)$ whose binary expansions disagree in a finite number of digits.

  comment

Representation Theory

• Paper 1, Section II, G

  Representation Theory | Part II, 2017

  (a) Prove that if there exists a faithful irreducible complex representation of a finite group $G$, then the centre $Z(G)$ is cyclic.

  (b) Define the permutations $a, b, c \in S_{6}$ by

  $$a=\left(\begin{array}{lll} 1 & 2 & 3 \end{array}\right), b=\left(\begin{array}{lll} 4 & 5 & 6 \end{array}\right), c=\left(\begin{array}{ll} 2 & 3 \end{array}\right)(45),$$

  and let $E=\langle a, b, c\rangle$.

  (i) Using the relations $a^{3}=b^{3}=c^{2}=1, a b=b a, c^{-1} a c=a^{-1}$ and $c^{-1} b c=b^{-1}$, prove that $E$ has order 18 .

  (ii) Suppose that $\varepsilon$ and $\eta$ are complex cube roots of unity. Prove that there is a (matrix) representation $\rho$ of $E$ over $\mathbb{C}$ such that

  $$a \mapsto\left(\begin{array}{cc} \varepsilon & 0 \\ 0 & \varepsilon^{-1} \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} \eta & 0 \\ 0 & \eta^{-1} \end{array}\right), \quad c \mapsto\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)$$

  (iii) For which values of $\varepsilon, \eta$ is $\rho$ faithful? For which values of $\varepsilon, \eta$ is $\rho$ irreducible?

  (c) Note that $\langle a, b\rangle$ is a normal subgroup of $E$ which is isomorphic to $C_{3} \times C_{3}$. By inducing linear characters of this subgroup, or otherwise, obtain the character table of $E$.

  Deduce that $E$ has the property that $Z(E)$ is cyclic but $E$ has no faithful irreducible representation over $\mathbb{C}$.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2017

  By considering the singularity at $\infty$, show that any injective analytic map $f: \mathbb{C} \rightarrow \mathbb{C}$ has the form $f(z)=a z+b$ for some $a \in \mathbb{C}^{*}$ and $b \in \mathbb{C}$.

  State the Riemann-Hurwitz formula for a non-constant analytic map $f: R \rightarrow S$ of compact Riemann surfaces $R$ and $S$, explaining each term that appears.

  Suppose $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ is analytic of degree 2. Show that there exist Möbius transformations $S$ and $T$ such that

  $$S f T: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$$

  is the map given by $z \mapsto z^{2}$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2017

  The dataset ChickWeights records the weight of a group of chickens fed four different diets at a range of time points. We perform the following regressions in $R$.

  

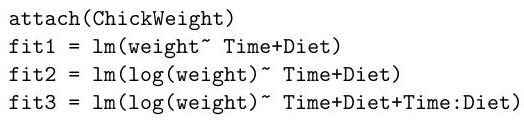
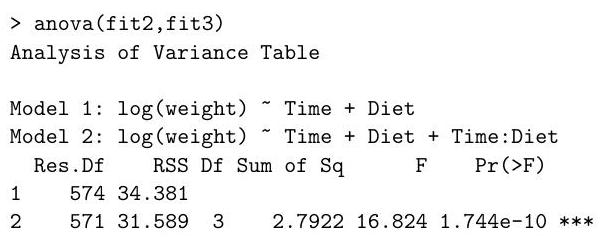
  (i) Which hypothesis test does the following command perform? State the degrees of freedom, and the conclusion of the test.

  

  (ii) Define a diagnostic plot that might suggest the logarithmic transformation of the response in fit2.

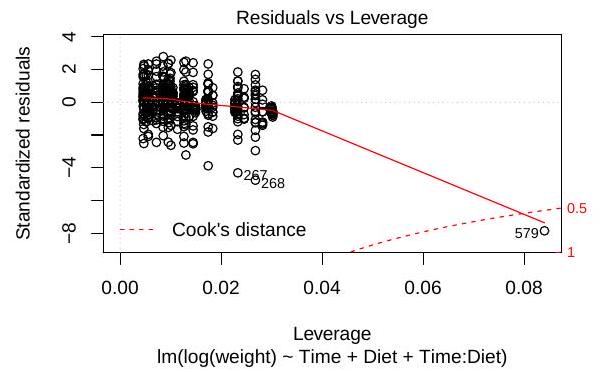
  (iii) Define the dashed line in the following plot, generated with the command plot(fit3). What does it tell us about the data point 579 ?

  

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2017

  The Cambridge Lawn Tennis Club organises a tournament in which every match consists of 11 games, all of which are played. The player who wins 6 or more games is declared the winner.

  For players $a$ and $b$, let $n_{a b}$ be the total number of games they play against each other, and let $y_{a b}$ be the number of these games won by player $a$. Let $\tilde{n}_{a b}$ and $\tilde{y}_{a b}$ be the corresponding number of matches.

  A statistician analysed the tournament data using a Binomial Generalised Linear Model (GLM) with outcome $y_{a b}$. The probability $P_{a b}$ that $a$ wins a game against $b$ is modelled by

  $$\log \left(\frac{P_{a b}}{1-P_{a b}}\right)=\beta_{a}-\beta_{b},$$

  with an appropriate corner point constraint. You are asked to re-analyse the data, but the game-level results have been lost and you only know which player won each match.

  We define a new GLM for the outcomes $\tilde{y}_{a b}$ with $\tilde{P}_{a b}=\mathbb{E} \tilde{y}_{a b} / \tilde{n}_{a b}$ and $g\left(\tilde{P}_{a b}\right)=$ $\beta_{a}-\beta_{b}$, where the $\beta_{a}$ are defined in $(*)$. That is, $\beta_{a}-\beta_{b}$ is the log-odds that $a$ wins a game against $b$, not a match.

  Derive the form of the new link function $g$. [You may express your answer in terms of a cumulative distribution function.]

  comment

Statistical Physics

• Paper 1, Section II, D

  Statistical Physics | Part II, 2017

  Explain what is meant by the microcanonical ensemble for a quantum system. Sketch how to derive the probability distribution for the canonical ensemble from the microcanonical ensemble. Under what physical conditions should each type of ensemble be used?

  A paramagnetic solid contains atoms with magnetic moment $\boldsymbol{\mu}=\mu_{B} \mathbf{J}$, where $\mu_{B}$ is a positive constant and $\mathbf{J}$ is the intrinsic angular momentum of the atom. In an applied magnetic field $\mathbf{B}$, the energy of an atom is $-\boldsymbol{\mu} \cdot \mathbf{B}$. Consider $\mathbf{B}=(0,0, B)$. Each atom has total angular momentum $J \in \mathbb{Z}$, so the possible values of $J_{z}=m \in \mathbb{Z}$ are $-J \leqslant m \leqslant J$.

  Show that the partition function for a single atom is

  $$Z_{1}(T, B)=\frac{\sinh \left(x\left(J+\frac{1}{2}\right)\right)}{\sinh (x / 2)}$$

  where $x=\mu_{B} B / k T$.

  Compute the average magnetic moment $\left\langle\mu_{z}\right\rangle$ of the atom. Sketch $\left\langle\mu_{z}\right\rangle / J$ for $J=1$, $J=2$ and $J=3$ on the same graph.

  The total magnetization is $M_{z}=N\left\langle\mu_{z}\right\rangle$, where $N$ is the number of atoms. The magnetic susceptibility is defined by

  $$\chi=\left(\frac{\partial M_{z}}{\partial B}\right)_{T}$$

  Show that the solid obeys Curie's law at high temperatures. Compute the susceptibility at low temperatures and give a physical explanation for the result.

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2017

  (a) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $\Delta_{0}, \Delta_{1}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $\mathbb{E}\left[\left|\Delta_{i}\right|\right]<\infty$ and $\mathbb{E}\left[\Delta_{i}\right]=0, i \geqslant 0$. Further, let

  $$X_{0}=\Delta_{0} \quad \text { and } \quad X_{n+1}=X_{n}+\Delta_{n+1} f_{n}\left(X_{0}, \ldots, X_{n}\right), \quad n \geqslant 0$$

  where

  $$f_{n}\left(x_{0}, \ldots, x_{n}\right)=\frac{1}{n+1} \sum_{i=0}^{n} x_{i}$$

  Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the natural filtration $\mathcal{F}_{n}=$ $\sigma\left(X_{0}, \ldots, X_{n}\right)$.

  (c) State and prove the optional stopping theorem for a bounded stopping time $\tau$.

  comment

Topics in Analysis

• Paper 1, Section I, 2F

  Topics in Analysis | Part II, 2017

  State Liouville's theorem on the approximation of algebraic numbers by rationals.

  Suppose that we have a sequence $\zeta_{n}$ with $\zeta_{n} \in\{0,1\}$. State and prove a necessary and sufficient condition on the $\zeta_{n}$ for

  $$\sum_{n=0}^{\infty} \zeta_{n} 10^{-n !}$$

  to be transcendental.

  comment

Waves

• Paper 1, Section II, B

  Waves | Part II, 2017

  Derive the wave equation governing the pressure disturbance $\tilde{p}$, for linearised, constant entropy sound waves in a compressible inviscid fluid of density $\rho_{0}$ and sound speed $c_{0}$, which is otherwise at rest.

  Consider a harmonic acoustic plane wave with wavevector $\mathbf{k}_{I}=k_{I}(\sin \theta, \cos \theta, 0)$ and unit-amplitude pressure disturbance. Determine the resulting velocity field $\mathbf{u}$.

  Consider such an acoustic wave incident from $y<0$ on a thin elastic plate at $y=0$. The regions $y<0$ and $y>0$ are occupied by gases with densities $\rho_{1}$ and $\rho_{2}$, respectively, and sound speeds $c_{1}$ and $c_{2}$, respectively. The kinematic boundary conditions at the plate are those appropriate for an inviscid fluid, and the (linearised) dynamic boundary condition is

  $$m \frac{\partial^{2} \eta}{\partial t^{2}}+B \frac{\partial^{4} \eta}{\partial x^{4}}+[\tilde{p}(x, 0, t)]_{-}^{+}=0$$

  where $m$ and $B$ are the mass and bending moment per unit area of the plate, and $y=\eta(x, t)$ (with $\left|\mathbf{k}_{I} \eta\right| \ll 1$ ) is its perturbed position. Find the amplitudes of the reflected and transmitted pressure perturbations, expressing your answers in terms of the dimensionless parameter

  $$\beta=\frac{k_{I} \cos \theta\left(m c_{1}^{2}-B k_{I}^{2} \sin ^{4} \theta\right)}{\rho_{1} c_{1}^{2}}$$

  (i) If $\rho_{1}=\rho_{2}=\rho_{0}$ and $c_{1}=c_{2}=c_{0}$, under what condition is the incident wave perfectly transmitted?

  (ii) If $\rho_{1} c_{1} \gg \rho_{2} c_{2}$, comment on the reflection coefficient, and show that waves incident at a sufficiently large angle are reflected as if from a pressure-release surface (i.e. an interface where $\tilde{p}=0$ ), no matter how large the plate mass and bending moment may be.

  comment