(a) (i) Define the push-out of the following diagram of groups.

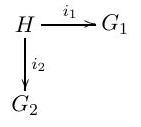
When is a push-out a free product with amalgamation?

(ii) State the Seifert-van Kampen theorem.

(b) Let $X=\mathbb{R} P^{2} \vee S^{1}$ (recalling that $\mathbb{R} P^{2}$ is the real projective plane), and let $x \in X$.

(i) Compute the fundamental group $\pi_{1}(X, x)$ of the space $X$.

(ii) Show that there is a surjective homomorphism $\phi: \pi_{1}(X, x) \rightarrow S_{3}$, where $S_{3}$ is the symmetric group on three elements.

(c) Let $\widehat{X} \rightarrow X$ be the covering space corresponding to the kernel of $\phi$.

(i) Draw $\widehat{X}$and justify your answer carefully.

(ii) Does $\widehat{X}$retract to a graph? Justify your answer briefly.

(iii) Does $\widehat{X}$deformation retract to a graph? Justify your answer briefly.