Part II, 2015, Paper 4

Algebraic Geometry

• Paper 4, Section II, F

  Algebraic Geometry | Part II, 2015

  (i) Explain how a linear system on a curve $C$ may induce a morphism from $C$ to projective space. What condition on the linear system is necessary to yield a morphism $f: C \rightarrow \mathbb{P}^{n}$ such that the pull-back of a hyperplane section is an element of the linear system? What condition is necessary to imply the morphism is an embedding?

  (ii) State the Riemann-Roch theorem for curves.

  (iii) Show that any divisor of degree 5 on a curve $C$ of genus 2 induces an embedding.

  comment

Algebraic Topology

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2015

  State the Mayer-Vietoris theorem for a simplicial complex $K$ which is the union of two subcomplexes $M$ and $N$. Explain briefly how the connecting homomorphism $\partial_{n}: H_{n}(K) \rightarrow H_{n-1}(M \cap N)$ is defined.

  If $K$ is the union of subcomplexes $M_{1}, M_{2}, \ldots, M_{n}$, with $n \geqslant 2$, such that each intersection

  $$M_{i_{1}} \cap M_{i_{2}} \cap \cdots \cap M_{i_{k}}, \quad 1 \leqslant k \leqslant n,$$

  is either empty or has the homology of a point, then show that

  $$H_{i}(K)=0 \quad \text { for } \quad i \geqslant n-1 .$$

  Construct examples for each $n \geqslant 2$ showing that this is sharp.

  comment

Applications of Quantum Mechanics

• Paper 4, Section II,

  Applications of Quantum Mechanics | Part II, 2015

  Let $\Lambda$ be a Bravais lattice with basis vectors $\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}$. Define the reciprocal lattice $\Lambda^{*}$ and write down basis vectors $\mathbf{b}_{1}, \mathbf{b}_{2}, \mathbf{b}_{3}$ for $\Lambda^{*}$ in terms of the basis for $\Lambda$.

  A finite crystal consists of identical atoms at sites of $\Lambda$ given by

  $$\ell=n_{1} \mathbf{a}_{1}+n_{2} \mathbf{a}_{2}+n_{3} \mathbf{a}_{3} \quad \text { with } \quad 0 \leqslant n_{i}<N_{i}$$

  A particle of mass $m$ scatters off the crystal; its wavevector is $\mathbf{k}$ before scattering and $\mathbf{k}^{\prime}$ after scattering, with $|\mathbf{k}|=\left|\mathbf{k}^{\prime}\right|$. Show that the scattering amplitude in the Born approximation has the form

  $$-\frac{m}{2 \pi \hbar^{2}} \Delta(\mathbf{q}) \tilde{U}(\mathbf{q}), \quad \mathbf{q}=\mathbf{k}^{\prime}-\mathbf{k}$$

  where $U(\mathbf{x})$ is the potential due to a single atom at the origin and $\Delta(\mathbf{q})$ depends on the crystal structure. [You may assume that in the Born approximation the amplitude for scattering off a potential $V(\mathbf{x})$ is $-\left(m / 2 \pi \hbar^{2}\right) \tilde{V}(\mathbf{q})$ where tilde denotes the Fourier transform.]

  Derive an expression for $|\Delta(\mathbf{q})|$ that is valid when $e^{-i \mathbf{q} \cdot \mathbf{a}_{i}} \neq 1$. Show also that when $\mathbf{q}$ is a reciprocal lattice vector $|\Delta(\mathbf{q})|$ is equal to the total number of atoms in the crystal. Comment briefly on the significance of these results.

  Now suppose that $\Lambda$ is a face-centred-cubic lattice:

  $$\mathbf{a}_{1}=\frac{a}{2}(\hat{\mathbf{y}}+\hat{\mathbf{z}}), \quad \mathbf{a}_{2}=\frac{a}{2}(\hat{\mathbf{z}}+\hat{\mathbf{x}}), \quad \mathbf{a}_{3}=\frac{a}{2}(\hat{\mathbf{x}}+\hat{\mathbf{y}})$$

  where $a$ is a constant. Show that for a particle incident with $|\mathbf{k}|>2 \pi / a$, enhanced scattering is possible for at least two values of the scattering angle, $\theta_{1}$ and $\theta_{2}$, related by

  $$\frac{\sin \left(\theta_{1} / 2\right)}{\sin \left(\theta_{2} / 2\right)}=\frac{\sqrt{3}}{2}$$

  comment

Applied Probability

• Paper 4, Section II, K

  Applied Probability | Part II, 2015

  (i) Let $X$ be a Markov chain on $S$ and $A \subset S$. Let $T_{A}$ be the hitting time of $A$ and $\tau_{y}$ denote the total time spent at $y \in S$ by the chain before hitting $A$. Show that if $h(x)=\mathbb{P}_{x}\left(T_{A}<\infty\right)$, then $\mathbb{E}_{x}\left[\tau_{y} \mid T_{A}<\infty\right]=[h(y) / h(x)] \mathbb{E}_{x}\left(\tau_{y}\right) .$

  (ii) Define the Moran model and show that if $X_{t}$ is the number of individuals carrying allele $a$ at time $t \geqslant 0$ and $\tau$ is the fixation time of allele $a$, then

  $$\mathbb{P}\left(X_{\tau}=N \mid X_{0}=i\right)=\frac{i}{N}$$

  Show that conditionally on fixation of an allele $a$ being present initially in $i$ individuals,

  $$\mathbb{E}[\tau \mid \text { fixation }]=N-i+\frac{N-i}{i} \sum_{j=1}^{i-1} \frac{j}{N-j}$$

  comment

Asymptotic Methods

• Paper 4, Section II, C

  Asymptotic Methods | Part II, 2015

  Consider the ordinary differential equation

  $$\frac{d^{2} u}{d z^{2}}+f(z) \frac{d u}{d z}+g(z) u=0$$

  where

  $$f(z) \sim \sum_{m=0}^{\infty} \frac{f_{m}}{z^{m}}, \quad g(z) \sim \sum_{m=0}^{\infty} \frac{g_{m}}{z^{m}}, \quad z \rightarrow \infty$$

  and $f_{m}, g_{m}$ are constants. Look for solutions in the asymptotic form

  $$u(z)=e^{\lambda z} z^{\mu}\left[1+\frac{a}{z}+\frac{b}{z^{2}}+O\left(\frac{1}{z^{3}}\right)\right], \quad z \rightarrow \infty$$

  and determine $\lambda$ in terms of $\left(f_{0}, g_{0}\right)$, as well as $\mu$ in terms of $\left(\lambda, f_{0}, f_{1}, g_{1}\right)$.

  Deduce that the Bessel equation

  $$\frac{d^{2} u}{d z^{2}}+\frac{1}{z} \frac{d u}{d z}+\left(1-\frac{\nu^{2}}{z^{2}}\right) u=0$$

  where $\nu$ is a complex constant, has two solutions of the form

  $$\begin{aligned} &u^{(1)}(z)=\frac{e^{i z}}{z^{1 / 2}}\left[1+\frac{a^{(1)}}{z}+O\left(\frac{1}{z^{2}}\right)\right], \quad z \rightarrow \infty \\ &u^{(2)}(z)=\frac{e^{-i z}}{z^{1 / 2}}\left[1+\frac{a^{(2)}}{z}+O\left(\frac{1}{z^{2}}\right)\right], \quad z \rightarrow \infty \end{aligned}$$

  and determine $a^{(1)}$ and $a^{(2)}$ in terms of $\nu .$

  Can the above asymptotic expansions be valid for all $\arg (z)$, or are they valid only in certain domains of the complex $z$-plane? Justify your answer briefly.

  comment

Classical Dynamics

• Paper 4, Section I, D

  Classical Dynamics | Part II, 2015

  A triatomic molecule is modelled by three masses moving in a line while connected to each other by two identical springs of force constant $k$ as shown in the figure.

  

  (a) Write down the Lagrangian and derive the equations describing the motion of the atoms.

  (b) Find the normal modes and their frequencies. What motion does the lowest frequency represent?

  comment

• Paper 4, Section II, C

  Classical Dynamics | Part II, 2015

  Consider a rigid body with angular velocity $\boldsymbol{\omega}$, angular momentum $\mathbf{L}$ and position vector $\mathbf{r}$, in its body frame.

  (a) Use the expression for the kinetic energy of the body,

  $$\frac{1}{2} \int d^{3} \mathbf{r} \rho(\mathbf{r}) \dot{\mathbf{r}}^{2},$$

  to derive an expression for the tensor of inertia of the body, I. Write down the relationship between $\mathbf{L}, \mathbf{I}$ and $\boldsymbol{\omega}$.

  (b) Euler's equations of torque-free motion of a rigid body are

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} \end{aligned}$$

  Working in the frame of the principal axes of inertia, use Euler's equations to show that the energy $E$ and the squared angular momentum $\mathbf{L}^{2}$ are conserved.

  (c) Consider a cuboid with sides $a, b$ and $c$, and with mass $M$ distributed uniformly.

  (i) Use the expression for the tensor of inertia derived in (a) to calculate the principal moments of inertia of the body.

  (ii) Assume $b=2 a$ and $c=4 a$, and suppose that the initial conditions are such that

  $$\mathbf{L}^{2}=2 I_{2} E$$

  with the initial angular velocity $\omega$ perpendicular to the intermediate principal axis $\mathbf{e}_{2}$. Derive the first order differential equation for $\omega_{2}$ in terms of $E, M$ and $a$ and hence determine the long-term behaviour of $\boldsymbol{\omega}$.

  comment

Coding and Cryptography

• Paper 4, Section I, G

  Coding and Cryptography | Part II, 2015

  Explain how to construct binary Reed-Muller codes. State and prove a result giving the minimum distance for each such Reed-Muller code.

  comment

Cosmology

• Paper 4, Section I, C

  Cosmology | Part II, 2015

  Calculate the total effective number of relativistic spin states $g_{*}$ present in the early universe when the temperature $T$ is $10^{10} \mathrm{~K}$ if there are three species of low-mass neutrinos and antineutrinos in addition to photons, electrons and positrons. If the weak interaction rate is $\Gamma=\left(T / 10^{10} \mathrm{~K}\right)^{5} \mathrm{~s}^{-1}$ and the expansion rate of the universe is $H=\sqrt{8 \pi G \rho / 3}$, where $\rho$ is the total density of the universe, calculate the temperature $T_{*}$ at which the neutrons and protons cease to interact via weak interactions, and show that $T_{*} \propto g_{*}^{1 / 6}$.

  State the formula for the equilibrium ratio of neutrons to protons at $T_{*}$, and briefly describe the sequence of events as the temperature falls from $T_{*}$ to the temperature at which the nucleosynthesis of helium and deuterium ends.

  What is the effect of an increase or decrease of $g_{*}$ on the abundance of helium-4 resulting from nucleosynthesis? Why do changes in $g_{*}$ have a very small effect on the final abundance of deuterium?

  comment

Differential Geometry

• Paper 4, Section II, G

  Differential Geometry | Part II, 2015

  Let $\mathrm{U}(n)$ denote the set of $n \times n$ unitary complex matrices. Show that $\mathrm{U}(n)$ is a smooth (real) manifold, and find its dimension. [You may use any general results from the course provided they are stated correctly.] For $A$ any matrix in $\mathrm{U}(n)$ and $H$ an $n \times n$ complex matrix, determine when $H$ represents a tangent vector to $\mathrm{U}(n)$ at $A$.

  Consider the tangent spaces to $\mathrm{U}(n)$ equipped with the metric induced from the standard (Euclidean) inner product $\langle\cdot, \cdot\rangle$ on the real vector space of $n \times n$ complex matrices, given by $\langle L, K\rangle=\operatorname{Re} \operatorname{trace}\left(L K^{*}\right)$, where $\operatorname{Re}$ denotes the real part and $K^{*}$ denotes the conjugate transpose of $K$. Suppose that $H$ represents a tangent vector to $\mathrm{U}(n)$ at the identity matrix $I$. Sketch an explicit construction of a geodesic curve on $\mathrm{U}(n)$ passing through $I$ and with tangent direction $H$, giving a brief proof that the acceleration of the curve is always orthogonal to the tangent space to $\mathrm{U}(n)$.

  [Hint: You will find it easier to work directly with $n \times n$ complex matrices, rather than the corresponding $2 n \times 2 n$ real matrices.]

  comment

Dynamical Systems

• Paper 4, Section II, B

  Dynamical Systems | Part II, 2015

  Let $f: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. Explain what is meant by the statements (i) that $f$ has a horseshoe and (ii) that $f$ is chaotic (according to Glendinning's definition).

  Assume that $f$ has a 3-cycle $\left\{x_{0}, x_{1}, x_{2}\right\}$ with $x_{1}=f\left(x_{0}\right), x_{2}=f\left(x_{1}\right), x_{0}=f\left(x_{2}\right)$ and, without loss of generality, $x_{0}<x_{1}<x_{2}$. Prove that $f^{2}$ has a horseshoe. [You may assume the intermediate value theorem.]

  Represent the effect of $f$ on the intervals $I_{a}=\left[x_{0}, x_{1}\right]$ and $I_{b}=\left[x_{1}, x_{2}\right]$ by means of a directed graph, explaining carefully how the graph is constructed. Explain what feature of the graph implies the existence of a 3-cycle.

  The map $g: I \rightarrow I$ has a 5-cycle $\left\{x_{0}, x_{1}, x_{2}, x_{3}, x_{4}\right\}$ with $x_{i+1}=g\left(x_{i}\right), 0 \leqslant i \leqslant 3$ and $x_{0}=g\left(x_{4}\right)$, and $x_{0}<x_{1}<x_{2}<x_{3}<x_{4}$. For which $n, 1 \leqslant n \leqslant 4$, is an $n$-cycle of $g$ guaranteed to exist? Is $g$ guaranteed to be chaotic? Is $g$ guaranteed to have a horseshoe? Justify your answers. [You may use a suitable directed graph as part of your arguments.]

  How do your answers to the above change if instead $x_{4}<x_{2}<x_{1}<x_{3}<x_{0}$ ?

  comment

Electrodynamics

• Paper 4, Section II, A

  Electrodynamics | Part II, 2015

  A point particle of charge $q$ has trajectory $y^{\mu}(\tau)$ in Minkowski space, where $\tau$ is its proper time. The resulting electromagnetic field is given by the Liénard-Wiechert 4-potential

  $$A^{\mu}(x)=-\frac{q \mu_{0} c}{4 \pi} \frac{u^{\mu}\left(\tau_{*}\right)}{R^{\nu}\left(\tau_{*}\right) u_{\nu}\left(\tau_{*}\right)}, \quad \text { where } \quad R^{\nu}=x^{\nu}-y^{\nu}(\tau) \quad \text { and } \quad u^{\mu}=d y^{\mu} / d \tau$$

  Write down the condition that determines the point $y^{\mu}\left(\tau_{*}\right)$ on the trajectory of the particle for a given value of $x^{\mu}$. Express this condition in terms of components, setting $x^{\mu}=(c t, \mathbf{x})$ and $y^{\mu}=\left(c t^{\prime}, \mathbf{y}\right)$, and define the retarded time $t_{r}$.

  Suppose that the 3 -velocity of the particle $\mathbf{v}\left(t^{\prime}\right)=\dot{\mathbf{y}}\left(t^{\prime}\right)=d \mathbf{y} / d t^{\prime}$ is small in size compared to $c$, and suppose also that $r=|\mathbf{x}| \gg|\mathbf{y}|$. Working to leading order in $1 / r$ and to first order in $\mathbf{v}$, show that

  $$\phi(x)=\frac{q \mu_{0} c}{4 \pi r}\left(c+\hat{\mathbf{r}} \cdot \mathbf{v}\left(t_{r}\right)\right), \quad \mathbf{A}(x)=\frac{q \mu_{0}}{4 \pi r} \mathbf{v}\left(t_{r}\right), \quad \text { where } \quad \hat{\mathbf{r}}=\mathbf{x} / r$$

  Now assume that $t_{r}$ can be replaced by $t_{-}=t-(r / c)$ in the expressions for $\phi$ and $\mathbf{A}$ above. Calculate the electric and magnetic fields to leading order in $1 / r$ and hence show that the Poynting vector is (in this approximation)

  $$\mathbf{N}(x)=\frac{q^{2} \mu_{0}}{(4 \pi)^{2} c} \frac{\hat{\mathbf{r}}}{r^{2}}\left|\hat{\mathbf{r}} \times \dot{\mathbf{v}}\left(t_{-}\right)\right|^{2}$$

  If the charge $q$ is performing simple harmonic motion $\mathbf{y}\left(t^{\prime}\right)=A \mathbf{n} \cos \omega t^{\prime}$, where $\mathbf{n}$ is a unit vector and $A \omega \ll c$, find the total energy radiated during one period of oscillation.

  comment

Fluid Dynamics II

• Paper 4, Section II, E

  Fluid Dynamics II | Part II, 2015

  A stationary inviscid fluid of thickness $h$ and density $\rho$ is located below a free surface at $y=h$ and above a deep layer of inviscid fluid of the same density in $y<0$ flowing with uniform velocity $U>0$ in the $\mathbf{e}_{x}$ direction. The base velocity profile is thus

  $$u=U, y<0 ; \quad u=0,0<y<h$$

  while the free surface at $y=h$ is maintained flat by gravity.

  By considering small perturbations of the vortex sheet at $y=0$ of the form $\eta=\eta_{0} e^{i k x+\sigma t}, k>0$, calculate the dispersion relationship between $k$ and $\sigma$ in the irrotational limit. By explicitly deriving that

  $$\operatorname{Re}(\sigma)=\pm \frac{\sqrt{\tanh (h k)}}{1+\tanh (h k)} U k$$

  deduce that the vortex sheet is unstable at all wavelengths. Show that the growth rates of the unstable modes are approximately $U k / 2$ when $h k \gg 1$ and $U k \sqrt{h k}$ when $h k \ll 1$.

  comment

Further Complex Methods

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2015

  Explain how the Papperitz symbol

  $$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha_{1} & \beta_{1} & \gamma_{1} & z \\ \alpha_{2} & \beta_{2} & \gamma_{2} & \end{array}\right\}$$

  represents a differential equation with certain properties. [You need not write down the differential equation explicitly.]

  The hypergeometric function $F(a, b, c ; z)$ is defined to be the solution of the equation given by the Papperitz symbol

  

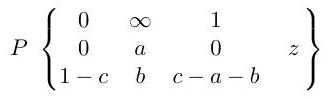
  that is analytic at $z=0$ and such that $F(a, b, c ; 0)=1$. Show that

  $$F(a, b, c ; z)=(1-z)^{-a} F\left(a, c-b, c ; \frac{z}{z-1}\right) \text {, }$$

  indicating clearly any general results for manipulating Papperitz symbols that you use.

  comment

Galois Theory

• Paper 4, Section II, $17 \mathrm{~F}$

  Galois Theory | Part II, 2015

  (i) Prove that a finite solvable extension $K \subseteq L$ of fields of characteristic zero is a radical extension.

  (ii) Let $x_{1}, \ldots, x_{7}$ be variables, $L=\mathbb{Q}\left(x_{1}, \ldots, x_{7}\right)$, and $K=\mathbb{Q}\left(e_{1}, \ldots, e_{7}\right)$ where $e_{i}$ are the elementary symmetric polynomials in the variables $x_{i}$. Is there an element $\alpha \in L$ such that $\alpha^{2} \in K$ but $\alpha \notin K$ ? Justify your answer.

  (iii) Find an example of a field extension $K \subseteq L$ of degree two such that $L \neq K(\sqrt{\alpha})$ for any $\alpha \in K$. Give an example of a field which has no extension containing an $11 t h$ primitive root of unity.

  comment

General Relativity

• Paper 4, Section II, D

  General Relativity | Part II, 2015

  In static spherically symmetric coordinates, the metric $g_{a b}$ for de Sitter space is given by

  $$d s^{2}=-\left(1-r^{2} / a^{2}\right) d t^{2}+\left(1-r^{2} / a^{2}\right)^{-1} d r^{2}+r^{2} d \Omega^{2}$$

  where $d \Omega^{2}=d \theta^{2}+\sin ^{2} \theta d \phi^{2}$ and $a$ is a constant.

  (a) Let $u=t-a \tanh ^{-1}(r / a)$ for $r \leqslant a$. Use the $(u, r, \theta, \phi)$ coordinates to show that the surface $r=a$ is non-singular. Is $r=0$ a space-time singularity?

  (b) Show that the vector field $g^{a b} u_{, a}$ is null.

  (c) Show that the radial null geodesics must obey either

  $$\frac{d u}{d r}=0 \quad \text { or } \quad \frac{d u}{d r}=-\frac{2}{1-r^{2} / a^{2}}$$

  Which of these families of geodesics is outgoing $(d r / d t>0) ?$

  Sketch these geodesics in the $(u, r)$ plane for $0 \leqslant r \leqslant a$, where the $r$-axis is horizontal and lines of constant $u$ are inclined at $45^{\circ}$ to the horizontal.

  (d) Show, by giving an explicit example, that an observer moving on a timelike geodesic starting at $r=0$ can cross the surface $r=a$ within a finite proper time.

  comment

Graph Theory

• Paper 4, Section II, I

  Graph Theory | Part II, 2015

  Let $G$ be a bipartite graph with vertex classes $X$ and $Y$. What does it mean to say that $G$ contains a matching from $X$ to $Y$ ? State and prove Hall's Marriage Theorem.

  Suppose now that every $x \in X$ has $d(x) \geqslant 1$, and that if $x \in X$ and $y \in Y$ with $x y \in E(G)$ then $d(x) \geqslant d(y)$. Show that $G$ contains a matching from $X$ to $Y$.

  comment

Linear Analysis

• Paper 4, Section II, G

  Linear Analysis | Part II, 2015

  Let $H$ be a Hilbert space and $T \in \mathcal{B}(H)$. Define what is meant by an adjoint of $T$ and prove that it exists, it is linear and bounded, and that it is unique. [You may use the Riesz Representation Theorem without proof.]

  What does it mean to say that $T$ is a normal operator? Give an example of a bounded linear map on $\ell_{2}$ that is not normal.

  Show that $T$ is normal if and only if $\|T x\|=\left\|T^{*} x\right\|$ for all $x \in H$.

  Prove that if $T$ is normal, then $\sigma(T)=\sigma_{\mathrm{ap}}(T)$, that is, that every element of the spectrum of $T$ is an approximate eigenvalue of $T$.

  comment

Logic and Set Theory

• Paper 4, Section II, I

  Logic and Set Theory | Part II, 2015

  State the Axiom of Foundation and the Principle of $\epsilon$-Induction, and show that they are equivalent (in the presence of the other axioms of $Z F$ ). [You may assume the existence of transitive closures.]

  Explain briefly how the Principle of $\epsilon$-Induction implies that every set is a member of some $V_{\alpha}$.

  Find the ranks of the following sets:

  (i) $\{\omega+1, \omega+2, \omega+3\}$,

  (ii) the Cartesian product $\omega \times \omega$,

  (iii) the set of all functions from $\omega$ to $\omega^{2}$.

  [You may assume standard properties of rank.]

  comment

Mathematical Biology

• Paper 4, Section I, E

  Mathematical Biology | Part II, 2015

  (i) A variant of the classic logistic population model is given by the HutchinsonWright equation

  $$\frac{d x(t)}{d t}=\alpha x(t)[1-x(t-T)]$$

  where $\alpha, T>0$. Determine the condition on $\alpha$ (in terms of $T$ ) for the constant solution $x(t)=1$ to be stable.

  (ii) Another variant of the logistic model is given by the equation

  $$\frac{d x(t)}{d t}=\alpha\left[x(t-T)-x(t)^{2}\right]$$

  where $\alpha, T>0$. Give a brief interpretation of what this model represents.

  Determine the condition on $\alpha$ (in terms of $T$ ) for the constant solution $x(t)=1$ to be stable in this model.

  comment

• Paper 4, Section II, E

  Mathematical Biology | Part II, 2015

  In a stochastic model of multiple populations, $P=P(\mathbf{x}, t)$ is the probability that the population sizes are given by the vector $\mathbf{x}$ at time $t$. The jump rate $W(\mathbf{x}, \mathbf{r})$ is the probability per unit time that the population sizes jump from $\mathbf{x}$ to $\mathbf{x}+\mathbf{r}$. Under suitable assumptions, the system may be approximated by the multivariate Fokker-Planck equation (with summation convention)

  $$\frac{\partial}{\partial t} P=-\frac{\partial}{\partial x_{i}} A_{i} P+\frac{1}{2} \frac{\partial^{2}}{\partial x_{i} \partial x_{j}} B_{i j} P$$

  where $A_{i}(\mathbf{x})=\sum_{\mathbf{r}} r_{i} W(\mathbf{x}, \mathbf{r})$ and matrix elements $B_{i j}(\mathbf{x})=\sum_{\mathbf{r}} r_{i} r_{j} W(\mathbf{x}, \mathbf{r})$.

  (a) Use the multivariate Fokker-Planck equation to show that

  $$\begin{aligned} \frac{d}{d t}\left\langle x_{k}\right\rangle &=\left\langle A_{k}\right\rangle \\ \frac{d}{d t}\left\langle x_{k} x_{l}\right\rangle &=\left\langle x_{l} A_{k}+x_{k} A_{l}+B_{k l}\right\rangle \end{aligned}$$

  [You may assume that $P(\mathbf{x}, t) \rightarrow 0$ as $|\mathbf{x}| \rightarrow \infty$.]

  (b) For small fluctuations, you may assume that the vector $\mathbf{A}$ may be approximated by a linear function in $\mathbf{x}$ and the matrix $\mathbf{B}$ may be treated as constant, i.e. $A_{k}(\mathbf{x}) \approx$ $a_{k l}\left(x_{l}-\left\langle x_{l}\right\rangle\right)$ and $B_{k l}(\mathbf{x}) \approx B_{k l}(\langle\mathbf{x}\rangle)=b_{k l}$ (where $a_{k l}$ and $b_{k l}$ are constants). Show that at steady state the covariances $C_{i j}=\operatorname{cov}\left(x_{i}, x_{j}\right)$ satisfy

  $$a_{i k} C_{j k}+a_{j k} C_{i k}+b_{i j}=0 .$$

  (c) A lab-controlled insect population consists of $x_{1}$ larvae and $x_{2}$ adults. Larvae are added to the system at rate $\lambda$. Larvae each mature at rate $\gamma$ per capita. Adults die at rate $\beta$ per capita. Give the vector $\mathbf{A}$ and matrix $\mathbf{B}$ for this model. Show that at steady state

  $$\left\langle x_{1}\right\rangle=\frac{\lambda}{\gamma}, \quad\left\langle x_{2}\right\rangle=\frac{\lambda}{\beta} .$$

  (d) Find the variance of each population size near steady state, and show that the covariance between the populations is zero.

  comment

Number Fields

• Paper 4, Section II, H

  Number Fields | Part II, 2015

  Let $K$ be a number field. State Dirichlet's unit theorem, defining all the terms you use, and what it implies for a quadratic field $\mathbb{Q}(\sqrt{d})$, where $d \neq 0,1$ is a square-free integer.

  Find a fundamental unit of $\mathbb{Q}(\sqrt{26})$.

  Find all integral solutions $(x, y)$ of the equation $x^{2}-26 y^{2}=\pm 10$.

  comment

Number Theory

• Paper 4, Section I, H

  Number Theory | Part II, 2015

  Show that if $10^{n}+1$ is prime then $n$ must be a power of 2 . Now assuming $n$ is a power of 2 , show that if $p$ is a prime factor of $10^{n}+1$ then $p \equiv 1(\bmod 2 n)$.

  Explain the method of Fermat factorization, and use it to factor $10^{4}+1$.

  comment

• Paper 4, Section II, H

  Number Theory | Part II, 2015

  State the Chinese Remainder Theorem.

  Let $N$ be an odd positive integer. Define the Jacobi symbol $\left(\frac{a}{N}\right)$. Which of the following statements are true, and which are false? Give a proof or counterexample as appropriate.

  (i) If $\left(\frac{a}{N}\right)=1$ then the congruence $x^{2} \equiv a(\bmod N)$ is soluble.

  (ii) If $N$ is not a square then $\sum_{a=1}^{N}\left(\frac{a}{N}\right)=0$.

  (iii) If $N$ is composite then there exists an integer a coprime to $N$ with

  $$a^{N-1} \not \equiv 1 \quad(\bmod N)$$

  (iv) If $N$ is composite then there exists an integer $a$ coprime to $N$ with

  $$a^{(N-1) / 2} \not \equiv\left(\frac{a}{N}\right) \quad(\bmod N)$$

  comment

Numerical Analysis

• Paper 4, Section II, E

  Numerical Analysis | Part II, 2015

  (a) Define the $m$ th Krylov space $K_{m}(A, v)$ for $A \in \mathbb{R}^{n \times n}$ and $0 \neq v \in \mathbb{R}^{n}$. Letting $\delta_{m}$ be the dimension of $K_{m}(A, v)$, prove the following results.

  (i) There exists a positive integer $s \leqslant n$ such that $\delta_{m}=m$ for $m \leqslant s$ and $\delta_{m}=s$ for $m>s$.

  (ii) If $v=\sum_{i=1}^{s^{\prime}} c_{i} w_{i}$, where $w_{i}$ are eigenvectors of $A$ for distinct eigenvalues and all $c_{i}$ are nonzero, then $s=s^{\prime}$.

  (b) Define the term residual in the conjugate gradient (CG) method for solving a system $A x=b$ with symmetric positive definite $A$. Explain (without proof) the connection to Krylov spaces and prove that for any right-hand side $b$ the CG method finds an exact solution after at most $t$ steps, where $t$ is the number of distinct eigenvalues of $A$. [You may use without proof known properties of the iterates of the CG method.]

  Define what is meant by preconditioning, and explain two ways in which preconditioning can speed up convergence. Can we choose the preconditioner so that the CG method requires only one step? If yes, is it a reasonable method for speeding up the computation?

  comment

Optimization and Control

• Paper 4, Section II, $25 K$

  Optimization and Control | Part II, 2015

  Consider the scalar system evolving as

  $$x_{t}=x_{t-1}+u_{t-1}+\epsilon_{t}, \quad t=1,2, \ldots,$$

  where $\left\{\epsilon_{t}\right\}_{t=1}^{\infty}$ is a white noise sequence with $E \epsilon_{t}=0$ and $E \epsilon_{t}^{2}=v$. It is desired to choose controls $\left\{u_{t}\right\}_{t=0}^{h-1}$ to minimize $E\left[\sum_{t=0}^{h-1}\left(\frac{1}{2} x_{t}^{2}+u_{t}^{2}\right)+x_{h}^{2}\right]$. Show that for $h=6$ the minimal cost is $x_{0}^{2}+6 v$.

  Find a constant $\lambda$ and a function $\phi$ which solve

  $$\phi(x)+\lambda=\min _{u}\left[\frac{1}{2} x^{2}+u^{2}+E \phi\left(x+u+\epsilon_{1}\right)\right]$$

  Let $P$ be the class of those policies for which every $u_{t}$ obeys the constraint $\left(x_{t}+u_{t}\right)^{2} \leqslant(0.9) x_{t}^{2}$. Show that $E_{\pi} \phi\left(x_{t}\right) \leqslant x_{0}^{2}+10 v$, for all $\pi \in P$. Find, and prove optimal, a policy which over all $\pi \in P$ minimizes

  $$\lim _{h \rightarrow \infty} \frac{1}{h} E_{\pi}\left[\sum_{t=0}^{h-1}\left(\frac{1}{2} x_{t}^{2}+u_{t}^{2}\right)\right]$$

  comment

Partial Differential Equations

• Paper 4, Section II, E

  Partial Differential Equations | Part II, 2015

  (a) Show that the Cauchy problem for $u(x, t)$ satisfying

  $$u_{t}+u=u_{x x}$$

  with initial data $u(x, 0)=u_{0}(x)$, which is a smooth $2 \pi$-periodic function of $x$, defines a strongly continuous one parameter semi-group of contractions on the Sobolev space $H_{\text {per }}^{s}$ for any $s \in\{0,1,2, \ldots\}$.

  (b) Solve the Cauchy problem for the equation

  $$u_{t t}+u_{t}+\frac{1}{4} u=u_{x x}$$

  with $u(x, 0)=u_{0}(x), u_{t}(x, 0)=u_{1}(x)$, where $u_{0}, u_{1}$ are smooth $2 \pi$-periodic functions of $x$, and show that the solution is smooth. Prove from first principles that the solution satisfies the property of finite propagation speed.

  [In this question all functions are real-valued, and

  $$H_{\text {per }}^{s}=\left\{u=\sum_{m \in \mathbb{Z}} \hat{u}(m) e^{i m x} \in L^{2}:\|u\|_{H^{s}}^{2}=\sum_{m \in \mathbb{Z}}\left(1+m^{2}\right)^{s}|\hat{u}(m)|^{2}<\infty\right\}$$

  are the Sobolev spaces of functions which are $2 \pi$-periodic in $x$, for $s=0,1,2, \ldots]$

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, A

  Principles of Quantum Mechanics | Part II, 2015

  The Hamiltonian for a quantum system in the Schrödinger picture is $H_{0}+\lambda V(t)$, where $H_{0}$ is independent of time and the parameter $\lambda$ is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Suppose that $|\chi\rangle$ and $|\phi\rangle$ are eigenstates of $H_{0}$ with distinct eigenvalues $E$ and $E^{\prime}$, respectively. Show that if the system is in state $|\chi\rangle$ at time zero then the probability of measuring it to be in state $|\phi\rangle$ at time $t$ is

  $$\frac{\lambda^{2}}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle\phi\left|V\left(t^{\prime}\right)\right| \chi\right\rangle e^{i\left(E^{\prime}-E\right) t^{\prime} / \hbar}\right|^{2}+O\left(\lambda^{3}\right)$$

  Let $H_{0}$ be the Hamiltonian for an isotropic three-dimensional harmonic oscillator of mass $m$ and frequency $\omega$, with $\chi(r)$ being the ground state wavefunction (where $r=|\mathbf{x}|$ ) and $\phi_{i}(\mathbf{x})=(2 m \omega / \hbar)^{1 / 2} x_{i} \chi(r)$ being wavefunctions for the states at the first excited energy level $(i=1,2,3)$. The oscillator is in its ground state at $t=0$ when a perturbation

  $$\lambda V(t)=\lambda \hat{x}_{3} e^{-\mu t}$$

  is applied, with $\mu>0$, and $H_{0}$ is then measured after a very large time has elapsed. Show that to first order in perturbation theory the oscillator will be found in one particular state at the first excited energy level with probability

  $$\frac{\lambda^{2}}{2 \hbar m \omega\left(\mu^{2}+\omega^{2}\right)},$$

  but that the probability that it will be found in either of the other excited states is zero (to this order).

  $\left[\right.$ You may use the fact that $\left.4 \pi \int_{0}^{\infty} r^{4}|\chi(r)|^{2} d r=\frac{3 \hbar}{2 m \omega} .\right]$

  comment

Principles of Statistics

• Paper 4, Section II, $\mathbf{2 4 J}$

  Principles of Statistics | Part II, 2015

  Given independent and identically distributed observations $X_{1}, \ldots, X_{n}$ with finite mean $E\left(X_{1}\right)=\mu$ and variance $\operatorname{Var}\left(X_{1}\right)=\sigma^{2}$, explain the notion of a bootstrap sample $X_{1}^{b}, \ldots, X_{n}^{b}$, and discuss how you can use it to construct a confidence interval $C_{n}$ for $\mu$.

  Suppose you can operate a random number generator that can simulate independent uniform random variables $U_{1}, \ldots, U_{n}$ on $[0,1]$. How can you use such a random number generator to simulate a bootstrap sample?

  Suppose that $\left(F_{n}: n \in \mathbb{N}\right)$ and $F$ are cumulative probability distribution functions defined on the real line, that $F_{n}(t) \rightarrow F(t)$ as $n \rightarrow \infty$ for every $t \in \mathbb{R}$, and that $F$ is continuous on $\mathbb{R}$. Show that, as $n \rightarrow \infty$,

  $$\sup _{t \in \mathbb{R}}\left|F_{n}(t)-F(t)\right| \rightarrow 0 .$$

  State (without proof) the theorem about the consistency of the bootstrap of the mean, and use it to give an asymptotic justification of the confidence interval $C_{n}$. That is, prove that as $n \rightarrow \infty, P^{\mathbb{N}}\left(\mu \in C_{n}\right) \rightarrow 1-\alpha$ where $P^{\mathbb{N}}$ is the joint distribution of $X_{1}, X_{2}, \ldots$

  [You may use standard facts of stochastic convergence and the Central Limit Theorem without proof.]

  comment

Probability and Measure

• Paper 4, Section II, J

  Probability and Measure | Part II, 2015

  (a) State Fatou's lemma.

  (b) Let $X$ be a random variable on $\mathbb{R}^{d}$ and let $\left(X_{k}\right)_{k=1}^{\infty}$ be a sequence of random variables on $\mathbb{R}^{d}$. What does it mean to say that $X_{k} \rightarrow X$ weakly?

  State and prove the Central Limit Theorem for i.i.d. real-valued random variables. [You may use auxiliary theorems proved in the course provided these are clearly stated.]

  (c) Let $X$ be a real-valued random variable with characteristic function $\varphi$. Let $\left(h_{n}\right)_{n=1}^{\infty}$ be a sequence of real numbers with $h_{n} \neq 0$ and $h_{n} \rightarrow 0$. Prove that if we have

  $$\liminf _{n \rightarrow \infty} \frac{2 \varphi(0)-\varphi\left(-h_{n}\right)-\varphi\left(h_{n}\right)}{h_{n}^{2}}<\infty$$

  then $\mathbb{E}\left[X^{2}\right]<\infty$

  comment

Representation Theory

• Paper 4, Section II, F

  Representation Theory | Part II, 2015

  (a) Let $S^{1}$ be the circle group. Assuming any required facts about continuous functions from real analysis, show that every 1-dimensional continuous representation of $S^{1}$ is of the form

  $$z \mapsto z^{n}$$

  for some $n \in \mathbb{Z}$.

  (b) Let $G=S U(2)$, and let $\rho_{V}$ be a continuous representation of $G$ on a finitedimensional vector space $V$.

  (i) Define the character $\chi_{V}$ of $\rho_{V}$, and show that $\chi_{V} \in \mathbb{N}\left[z, z^{-1}\right]$.

  (ii) Show that $\chi_{V}(z)=\chi_{V}\left(z^{-1}\right)$.

  (iii) Let $V$ be the irreducible 4-dimensional representation of $G$. Decompose $V \otimes V$ into irreducible representations. Hence decompose the exterior square $\Lambda^{2} V$ into irreducible representations.

  comment

Statistical Modelling

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2015

  Data on 173 nesting female horseshoe crabs record for each crab its colour as one of 4 factors (simply labelled $1, \ldots, 4$ ), its width (in $\mathrm{cm}$ ) and the presence of male crabs nearby (a 1 indicating presence). The data are collected into the $\mathrm{R}$ data frame crabs and the first few lines are displayed below.

  

  Describe the model being fitted by the $\mathrm{R}$ command below.

  $>$ fit1 <- glm(males colour + width, family = binomial, data=crabs)

  The following (abbreviated) output is obtained from the summary command.

  

  Write out the calculation for an approximate $95 \%$ confidence interval for the coefficient for width. Describe the calculation you would perform to obtain an estimate of the probability that a female crab of colour 3 and with a width of $20 \mathrm{~cm}$ has males nearby. [You need not actually compute the end points of the confidence interval or the estimate of the probability above, but merely show the calculations that would need to be performed in order to arrive at them.]

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2015

  Consider the normal linear model where the $n$-vector of responses $Y$ satisfies $Y=X \beta+\varepsilon$ with $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Here $X$ is an $n \times p$ matrix of predictors with full column rank where $p \geqslant 3$ and $\beta \in \mathbb{R}^{p}$ is an unknown vector of regression coefficients. For $j \in\{1, \ldots, p\}$, denote the $j$ th column of $X$ by $X_{j}$, and let $X_{-j}$ be $X$ with its $j$ th column removed. Suppose $X_{1}=1_{n}$ where $1_{n}$ is an $n$-vector of 1 's. Denote the maximum likelihood estimate of $\beta$ by $\beta$. Write down the formula for $\hat{\beta}_{j}$ involving $P_{-j}$, the orthogonal projection onto the column space of $X_{-j}$.

  Consider $j, k \in\{2, \ldots, p\}$ with $j<k$. By thinking about the orthogonal projection of $X_{j}$ onto $X_{k}$, show that

  $$\operatorname{var}\left(\hat{\beta}_{j}\right) \geqslant \frac{\sigma^{2}}{\left\|X_{j}\right\|^{2}}\left(1-\left(\frac{X_{k}^{T} X_{j}}{\left\|X_{k}\right\|\left\|X_{j}\right\|}\right)^{2}\right)^{-1}$$

  [You may use standard facts about orthogonal projections including the fact that if $V$ and $W$ are subspaces of $\mathbb{R}^{n}$ with $V$ a subspace of $W$ and $\Pi_{V}$ and $\Pi_{W}$ denote orthogonal projections onto $V$ and $W$ respectively, then for all $v \in \mathbb{R}^{n},\left\|\Pi_{W} v\right\|^{2} \geqslant\left\|\Pi_{V} v\right\|^{2}$.]

  By considering the fitted values $X \hat{\beta}$, explain why if, for any $j \geqslant 2$, a constant is added to each entry in the $j$ th column of $X$, then $\hat{\beta}_{j}$ will remain unchanged. Let $\bar{X}_{j}=\sum_{i=1}^{n} X_{i j} / n$. Why is (*) also true when all instances of $X_{j}$ and $X_{k}$ are replaced by $X_{j}-\bar{X}_{j} 1_{n}$ and $X_{k}-\bar{X}_{k} 1_{n}$ respectively?

  The marks from mid-year statistics and mathematics tests and an end-of-year statistics exam are recorded for 100 secondary school students. The first few lines of the data are given below.

  

  The following abbreviated output is obtained:

  

  What are the hypothesis tests corresponding to the final column of the coefficients table? What is the hypothesis test corresponding to the final line of the output? Interpret the results when testing at the $5 \%$ level.

  How does the following sample correlation matrix for the data help to explain the relative sizes of some of the $p$-values?

  

  comment

Statistical Physics

• Paper 4, Section II, C

  Statistical Physics | Part II, 2015

  The Ising model consists of $N$ particles, labelled by $i$, arranged on a $D$-dimensional Euclidean lattice with periodic boundary conditions. Each particle has spin up $s_{i}=+1$, or down $s_{i}=-1$, and the energy in the presence of a magnetic field $B$ is

  $$E=-B \sum_{i} s_{i}-J \sum_{\langle i, j\rangle} s_{i} s_{j}$$

  where $J>0$ is a constant and $\langle i, j\rangle$ indicates that the second sum is over each pair of nearest neighbours (every particle has $2 D$ nearest neighbours). Let $\beta=1 / k_{B} T$, where $T$ is the temperature.

  (i) Express the average spin per particle, $m=\left(\sum_{i}\left\langle s_{i}\right\rangle\right) / N$, in terms of the canonical partition function $Z$.

  (ii) Show that in the mean-field approximation

  $$Z=C\left[Z_{1}\left(\beta B_{\mathrm{eff}}\right)\right]^{N}$$

  where $Z_{1}$ is a single-particle partition function, $B_{\text {eff }}$ is an effective magnetic field which you should find in terms of $B, J, D$ and $m$, and $C$ is a prefactor which you should also evaluate.

  (iii) Deduce an equation that determines $m$ for general values of $B, J$ and temperature $T$. Without attempting to solve for $m$ explicitly, discuss how the behaviour of the system depends on temperature when $B=0$, deriving an expression for the critical temperature $T_{c}$ and explaining its significance.

  (iv) Comment briefly on whether the results obtained using the mean-field approximation for $B=0$ are consistent with an expression for the free energy of the form

  $$F(m, T)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $a$ and $b$ are positive constants.

  comment

Stochastic Financial Models

• Paper 4, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models | Part II, 2015

  (i) An investor in a single-period market with time- 0 wealth $w_{0}$ may generate any time-1 wealth $w_{1}$ of the form $w_{1}=w_{0}+X$, where $X$ is any element of a vector space $V$ of random variables. The investor's objective is to maximize $E\left[U\left(w_{1}\right)\right]$, where $U$ is strictly increasing, concave and $C^{2}$. Define the utility indifference price $\pi(Y)$ of a random variable $Y$.

  Prove that the map $Y \mapsto \pi(Y)$ is concave. [You may assume that any supremum is attained.]

  (ii) Agent $j$ has utility $U_{j}(x)=-\exp \left(-\gamma_{j} x\right), j=1, \ldots, J$. The agents may buy for time- 0 price $p$ a risky asset which will be worth $X$ at time 1 , where $X$ is random and has density

  $$f(x)=\frac{1}{2} \alpha e^{-\alpha|x|}, \quad-\infty<x<\infty .$$

  Assuming zero interest, prove that agent $j$ will optimally choose to buy

  $$\theta_{j}=-\frac{\sqrt{1+p^{2} \alpha^{2}}-1}{\gamma_{j} p}$$

  units of the risky asset at time 0 .

  If the asset is in unit net supply, if $\Gamma^{-1} \equiv \sum_{j} \gamma_{j}^{-1}$, and if $\alpha>\Gamma$, prove that the market for the risky asset will clear at price

  $$p=-\frac{2 \Gamma}{\alpha^{2}-\Gamma^{2}}$$

  What happens if $\alpha \leqslant \Gamma ?$

  comment

Topics in Analysis

• Paper 4, Section I, $2 I$

  Topics in Analysis | Part II, 2015

  Let $\mathcal{K}$ be the set of all non-empty compact subsets of $m$-dimensional Euclidean space $\mathbb{R}^{m}$. Define the Hausdorff metric on $\mathcal{K}$, and prove that it is a metric.

  Let $K_{1} \supseteq K_{2} \supseteq \ldots$ be a sequence in $\mathcal{K}$. Show that $K=\bigcap_{n=1}^{\infty} K_{n}$ is also in $\mathcal{K}$ and that $K_{n} \rightarrow K$ as $n \rightarrow \infty$ in the Hausdorff metric.

  comment

Waves

• Paper 4, Section II, 36B

  Waves | Part II, 2015

  The shallow-water equations

  $$\frac{\partial h}{\partial t}+u \frac{\partial h}{\partial x}+h \frac{\partial u}{\partial x}=0, \quad \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+g \frac{\partial h}{\partial x}=0$$

  describe one-dimensional flow over a horizontal boundary with depth $h(x, t)$ and velocity $u(x, t)$, where $g$ is the acceleration due to gravity.

  Show that the Riemann invariants $u \pm 2\left(c-c_{0}\right)$ are constant along characteristics $C_{\pm}$satisfying $d x / d t=u \pm c$, where $c(h)$ is the linear wave speed and $c_{0}$ denotes a reference state.

  An initially stationary pool of fluid of depth $h_{0}$ is held between a stationary wall at $x=a>0$ and a removable barrier at $x=0$. At $t=0$ the barrier is instantaneously removed allowing the fluid to flow into the region $x<0$.

  For $0 \leqslant t \leqslant a / c_{0}$, find $u(x, t)$ and $c(x, t)$ in each of the regions

  $$\begin{gathered} \text { (i) } \quad c_{0} t \leqslant x \leqslant a \\ \text { (ii) }-2 c_{0} t \leqslant x \leqslant c_{0} t \end{gathered}$$

  explaining your argument carefully with a sketch of the characteristics in the $(x, t)$ plane.

  For $t \geqslant a / c_{0}$, show that the solution in region (ii) above continues to hold in the region $-2 c_{0} t \leqslant x \leqslant 3 a\left(c_{0} t / a\right)^{1 / 3}-2 c_{0} t$. Explain why this solution does not hold in $3 a\left(c_{0} t / a\right)^{1 / 3}-2 c_{0} t<x<a .$

  comment