Part II, 2015, Paper 3

Algebraic Geometry

• Paper 3, Section II, F

  Algebraic Geometry | Part II, 2015

  (i) Let $X$ be an affine variety. Define the tangent space of $X$ at a point $P$. Say what it means for the variety to be singular at $P$.

  (ii) Find the singularities of the surface in $\mathbb{P}^{3}$ given by the equation

  $$x y z+y z w+z w x+w x y=0 .$$

  (iii) Consider $C=Z\left(x^{2}-y^{3}\right) \subseteq \mathbb{A}^{2}$. Let $X \rightarrow \mathbb{A}^{2}$ be the blowup of the origin. Compute the proper transform of $C$ in $X$, and show it is non-singular.

  comment

Algebraic Topology

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2015

  Let $K$ and $L$ be simplicial complexes. Explain what is meant by a simplicial approximation to a continuous map $f:|K| \rightarrow|L|$. State the simplicial approximation theorem, and define the homomorphism induced on homology by a continuous map between triangulable spaces. [You do not need to show that the homomorphism is welldefined.]

  Let $h: S^{1} \rightarrow S^{1}$ be given by $z \mapsto z^{n}$ for a positive integer $n$, where $S^{1}$ is considered as the unit complex numbers. Compute the map induced by $h$ on homology.

  comment

Applications of Quantum Mechanics

• Paper 3, Section II, A

  Applications of Quantum Mechanics | Part II, 2015

  A particle of mass $m$ and energy $E=-\hbar^{2} \kappa^{2} / 2 m<0$ moves in one dimension subject to a periodic potential

  $$V(x)=-\frac{\hbar^{2} \lambda}{m} \sum_{\ell=-\infty}^{\infty} \delta(x-\ell a) \quad \text { with } \quad \lambda>0 .$$

  Determine the corresponding Floquet matrix $\mathcal{M}$. [You may assume without proof that for the Schrödinger equation with potential $\alpha \delta(x)$ the wavefunction $\psi(x)$ is continuous at $x=0$ and satisfies $\left.\psi^{\prime}(0+)-\psi^{\prime}(0-)=\left(2 m \alpha / \hbar^{2}\right) \psi(0) .\right]$

  Explain briefly, with reference to Bloch's theorem, how restrictions on the energy of a Bloch state can be derived from $\mathcal{M}$. Deduce that for the potential $V(x)$ above, $\kappa$ is confined to a range whose boundary values are determined by

  $$\tanh \left(\frac{\kappa a}{2}\right)=\frac{\kappa}{\lambda} \quad \text { and } \quad \operatorname{coth}\left(\frac{\kappa a}{2}\right)=\frac{\kappa}{\lambda} .$$

  Sketch the left-hand and right-hand sides of each of these equations as functions of $y=\kappa a / 2$. Hence show that there is exactly one allowed band of negative energies with either (i) $E_{-} \leqslant E<0$ or (ii) $E_{-} \leqslant E \leqslant E_{+}<0$ and determine the values of $\lambda a$ for which each of these cases arise. [You should not attempt to evaluate the constants $E_{\pm} .$]

  Comment briefly on the limit $a \rightarrow \infty$ with $\lambda$ fixed.

  comment

Applied Probability

• Paper 3, Section II, K

  Applied Probability | Part II, 2015

  (i) Let $X$ be a Poisson process of parameter $\lambda$. Let $Y$ be obtained by taking each point of $X$ and, independently of the other points, keeping it with probability $p$. Show that $Y$ is another Poisson process and find its intensity. Show that for every fixed $t$ the random variables $Y_{t}$ and $X_{t}-Y_{t}$ are independent.

  (ii) Suppose we have $n$ bins, and balls arrive according to a Poisson process of rate 1 . Upon arrival we choose a bin uniformly at random and place the ball in it. We let $M_{n}$ be the maximum number of balls in any bin at time $n$. Show that

  $$\mathbb{P}\left(M_{n} \geqslant(1+\epsilon) \frac{\log n}{\log \log n}\right) \rightarrow 0 \quad \text { as } n \rightarrow \infty$$

  [You may use the fact that if $\xi$ is a Poisson random variable of mean 1 , then

  $$\mathbb{P}(\xi \geqslant x) \leqslant \exp (x-x \log x) .]$$

  comment

Asymptotic Methods

• Paper 3, Section II, $27 \mathrm{C}$

  Asymptotic Methods | Part II, 2015

  Show that

  $$\int_{0}^{1} e^{i k t^{3}} d t=I_{1}-I_{2}, \quad k>0$$

  where $I_{1}$ is an integral from 0 to $\infty$ along the line $\arg (z)=\frac{\pi}{6}$ and $I_{2}$ is an integral from 1 to $\infty$ along a steepest-descent contour $C$ which you should determine.

  By employing in the integrals $I_{1}$ and $I_{2}$ the changes of variables $u=-i z^{3}$ and $u=-i\left(z^{3}-1\right)$, respectively, compute the first two terms of the large $k$ asymptotic expansion of the integral above.

  comment

Classical Dynamics

• Paper 3, Section I, $7 \mathrm{D}$

  Classical Dynamics | Part II, 2015

  (a) Consider a particle of mass $m$ that undergoes periodic motion in a one-dimensional potential $V(q)$. Write down the Hamiltonian $H(p, q)$ for the system. Explain what is meant by the angle-action variables $(\theta, I)$ of the system and write down the integral expression for the action variable $I$.

  (b) For $V(q)=\frac{1}{2} m \omega^{2} q^{2}$ and fixed total energy $E$, describe the shape of the trajectories in phase-space. By using the expression for the area enclosed by the trajectory, or otherwise, find the action variable $I$ in terms of $\omega$ and $E$. Hence describe how $E$ changes with $\omega$ if $\omega$ varies slowly with time. Justify your answer.

  comment

Coding and Cryptography

• Paper 3, Section I, G

  Coding and Cryptography | Part II, 2015

  Let $A$ be a random variable that takes each value $a$ in the finite alphabet $\mathcal{A}$ with probability $p(a)$. Show that, if each $l(a)$ is an integer greater than 0 and $\sum 2^{-l(a)} \leqslant 1$, then there is a decodable binary code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ with each codeword $c(a)$ having length $l(a)$.

  Prove that, for any decodable code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$, we have

  $$H(A) \leqslant \mathbb{E} l(A)$$

  where $H(A)$ is the entropy of the random variable $A$. When is there equality in this inequality?

  comment

Cosmology

• Paper 3, Section I, C

  Cosmology | Part II, 2015

  What is the flatness problem? Show by reference to the Friedmann equation how a period of accelerated expansion of the scale factor $a(t)$ in the early stages of the universe can solve the flatness problem if $\rho+3 P<0$, where $\rho$ is the mass density and $P$ is the pressure.

  In the very early universe, where we can neglect the spatial curvature and the cosmological constant, there is a homogeneous scalar field $\phi$ with a vacuum potential energy

  $$V(\phi)=m^{2} \phi^{2},$$

  and the Friedmann energy equation (in units where $8 \pi G=1$ ) is

  $$3 H^{2}=\frac{1}{2} \dot{\phi}^{2}+V(\phi),$$

  where $H$ is the Hubble parameter. The field $\phi$ obeys the evolution equation

  $$\ddot{\phi}+3 H \dot{\phi}+\frac{d V}{d \phi}=0$$

  During inflation, $\phi$ evolves slowly after starting from a large initial value $\phi_{i}$ at $t=0$. State what is meant by the slow-roll approximation. Show that in this approximation,

  $$\begin{aligned} \phi(t) &=\phi_{i}-\frac{2}{\sqrt{3}} m t \\ a(t) &=a_{i} \exp \left[\frac{m \phi_{i}}{\sqrt{3}} t-\frac{1}{3} m^{2} t^{2}\right]=a_{i} \exp \left[\frac{\phi_{i}^{2}-\phi^{2}(t)}{4}\right] \end{aligned}$$

  where $a_{i}$ is the initial value of $a$.

  As $\phi(t)$ decreases from its initial value $\phi_{i}$, what is its approximate value when the slow-roll approximation fails?

  comment

• Paper 3, Section II, C

  Cosmology | Part II, 2015

  Massive particles and antiparticles each with mass $m$ and respective number densities $n(t)$ and $\bar{n}(t)$ are present at time $t$ in the radiation era of an expanding universe with zero curvature and no cosmological constant. Assuming they interact with crosssection $\sigma$ at speed $v$, explain, by identifying the physical significance of each of the terms, why the evolution of $n(t)$ is described by

  $$\frac{d n}{d t}=-3 \frac{\dot{a}}{a} n-\langle\sigma v\rangle n \bar{n}+P(t)$$

  where the expansion scale factor of the universe is $a(t)$, and where the meaning of $P(t)$ should be briefly explained. Show that

  $$(n-\bar{n}) a^{3}=\text { constant }$$

  Assuming initial particle-antiparticle symmetry, show that

  $$\frac{d\left(n a^{3}\right)}{d t}=\langle\sigma v\rangle\left(n_{\mathrm{eq}}^{2}-n^{2}\right) a^{3}$$

  where $n_{\mathrm{eq}}$ is the equilibrium number density at temperature $T$.

  Let $Y=n / T^{3}$ and $x=m / T$. Show that

  $$\frac{d Y}{d x}=-\frac{\lambda}{x^{2}}\left(Y^{2}-Y_{\mathrm{eq}}^{2}\right)$$

  where $\lambda=m^{3}\langle\sigma v\rangle / H_{m}$ and $H_{m}$ is the Hubble expansion rate when $T=m$.

  When $x>x_{f} \simeq 10$, the number density $n$ can be assumed to be depleted only by annihilations. If $\lambda$ is constant, show that as $x \rightarrow \infty$ at late time, $Y$ approaches a constant value given by

  $$Y=\frac{x_{f}}{\lambda}$$

  Why do you expect weakly interacting particles to survive in greater numbers than strongly interacting particles?

  comment

Differential Geometry

• Paper 3 , Section II, G

  Differential Geometry | Part II, 2015

  Show that the surface $S$ of revolution $x^{2}+y^{2}=\cosh ^{2} z$ in $\mathbb{R}^{3}$ is homeomorphic to a cylinder and has everywhere negative Gaussian curvature. Show moreover the existence of a closed geodesic on $S$.

  Let $S \subset \mathbb{R}^{3}$ be an arbitrary embedded surface which is homeomorphic to a cylinder and has everywhere negative Gaussian curvature. By using a suitable version of the Gauss-Bonnet theorem, show that $S$ contains at most one closed geodesic. [If required, appropriate forms of the Jordan curve theorem in the plane may also be used without proof.

  comment

Dynamical Systems

• Paper 3, Section II, B

  Dynamical Systems | Part II, 2015

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=-\mu+x^{2}-y \\ &\dot{y}=y(a-x) \end{aligned}$$

  where $a$ is to be regarded as a fixed real constant and $\mu$ as a real parameter.

  Find the fixed points of the system and determine the stability of the system linearized about the fixed points. Hence identify the values of $\mu$ at given $a$ where bifurcations occur.

  Describe informally the concepts of centre manifold theory and apply it to analyse the bifurcations that occur in the above system with $a=1$. In particular, for each bifurcation derive an equation for the dynamics on the extended centre manifold and hence classify the bifurcation.

  What can you say, without further detailed calculation, about the case $a=0$ ?

  comment

Electrodynamics

• Paper 3, Section II, 34A

  Electrodynamics | Part II, 2015

  (i) Consider the action

  $$S=-\frac{1}{4 \mu_{0} c} \int\left(F_{\mu \nu} F^{\mu \nu}+2 \lambda^{2} A_{\mu} A^{\mu}\right) d^{4} x+\frac{1}{c} \int A_{\mu} J^{\mu} d^{4} x$$

  where $A_{\mu}(x)$ is a 4-vector potential, $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ is the field strength tensor, $J^{\mu}(x)$ is a conserved current, and $\lambda \geqslant 0$ is a constant. Derive the field equation

  $$\partial_{\mu} F^{\mu \nu}-\lambda^{2} A^{\nu}=-\mu_{0} J^{\nu} .$$

  For $\lambda=0$ the action $S$ describes standard electromagnetism. Show that in this case the theory is invariant under gauge transformations of the field $A_{\mu}(x)$, which you should define. Is the theory invariant under these same gauge transformations when $\lambda>0$ ?

  Show that when $\lambda>0$ the field equation above implies

  $$\partial_{\mu} \partial^{\mu} A^{\nu}-\lambda^{2} A^{\nu}=-\mu_{0} J^{\nu}$$

  Under what circumstances does $(*)$ hold in the case $\lambda=0$ ?

  (ii) Now suppose that $A_{\mu}(x)$ and $J_{\mu}(x)$ obeying $(*)$ reduce to static 3 -vectors $\mathbf{A}(\mathbf{x})$ and $\mathbf{J}(\mathbf{x})$ in some inertial frame. Show that there is a solution

  $$\mathbf{A}(\mathbf{x})=-\mu_{0} \int G\left(\left|\mathbf{x}-\mathbf{x}^{\prime}\right|\right) \mathbf{J}\left(\mathbf{x}^{\prime}\right) d^{3} \mathbf{x}^{\prime}$$

  for a suitable Green's function $G(R)$ with $G(R) \rightarrow 0$ as $R \rightarrow \infty$. Determine $G(R)$ for any $\lambda \geqslant 0$. [Hint: You may find it helpful to consider first the case $\lambda=0$ and then the case $\lambda>0$, using the result $\nabla^{2}\left(\frac{1}{R} f(R)\right)=\nabla^{2}\left(\frac{1}{R}\right) f(R)+\frac{1}{R} f^{\prime \prime}(R)$, where $\left.R=\left|\mathbf{x}-\mathbf{x}^{\prime}\right| .\right]$

  If $\mathbf{J}(\mathbf{x})$ is zero outside some bounded region, comment on the effect of the value of $\lambda$ on the behaviour of $\mathbf{A}(\mathbf{x})$ when $|\mathbf{x}|$ is large. [No further detailed calculations are required.]

  comment

Fluid Dynamics II

• Paper 3, Section II, E

  Fluid Dynamics II | Part II, 2015

  Consider a three-dimensional high-Reynolds number jet without swirl induced by a force $\mathbf{F}=F \mathbf{e}_{z}$ imposed at the origin in a fluid at rest. The velocity in the jet, described using cylindrical coordinates $(r, \theta, z)$, is assumed to remain steady and axisymmetric, and described by a boundary layer analysis.

  (i) Explain briefly why the flow in the jet can be described by the boundary layer equations

  $$u_{r} \frac{\partial u_{z}}{\partial r}+u_{z} \frac{\partial u_{z}}{\partial z}=\nu \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{z}}{\partial r}\right)$$

  (ii) Show that the momentum flux in the jet, $F=\int_{S} \rho u_{z}^{2} d S$, where $S$ is an infinite surface perpendicular to $\mathbf{e}_{z}$, is not a function of $z$. Combining this result with scalings from the boundary layer equations, derive the scalings for the unknown width $\delta(z)$ and typical velocity $U(z)$ of the jet as functions of $z$ and the other parameters of the problem $(\rho, \nu, F)$.

  (iii) Solving for the flow using a self-similar Stokes streamfunction

  $$\psi(r, z)=U(z) \delta^{2}(z) f(\eta), \quad \eta=r / \delta(z)$$

  show that $f(\eta)$ satisfies the differential equation

  $$f f^{\prime}-\eta\left(f^{\prime 2}+f f^{\prime \prime}\right)=f^{\prime}-\eta f^{\prime \prime}+\eta^{2} f^{\prime \prime \prime} .$$

  What boundary conditions should be applied to this equation? Give physical reasons for them.

  [Hint: In cylindrical coordinates for axisymmetric incompressible flow $\left(u_{r}(r, z), 0, u_{z}(r, z)\right)$ you are given the incompressibility condition as

  $$\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{\partial u_{z}}{\partial z}=0$$

  the $z$-component of the Navier-Stokes equation as

  $$\rho\left(\frac{\partial u_{z}}{\partial t}+u_{r} \frac{\partial u_{z}}{\partial r}+u_{z} \frac{\partial u_{z}}{\partial z}\right)=-\frac{\partial p}{\partial z}+\mu\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{z}}{\partial r}\right)+\frac{\partial^{2} u_{z}}{\partial z^{2}}\right]$$

  and the relationship between the Stokes streamfunction, $\psi(r, z)$, and the velocity components as

  $$\left.u_{r}=-\frac{1}{r} \frac{\partial \psi}{\partial z}, \quad u_{z}=\frac{1}{r} \frac{\partial \psi}{\partial r}\right]$$

  comment

Further Complex Methods

• Paper 3, Section $I$, B

  Further Complex Methods | Part II, 2015

  Define what is meant by the Cauchy principal value in the particular case

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{\cos x}{x^{2}-a^{2}} d x$$

  where the constant $a$ is real and strictly positive. Evaluate this expression explicitly, stating clearly any standard results involving contour integrals that you use.

  comment

Galois Theory

• Paper 3, Section II, F

  Galois Theory | Part II, 2015

  Let $f \in \mathbb{Q}[t]$ be of degree $n>0$, with no repeated roots, and let $L$ be a splitting field for $f$.

  (i) Show that $f$ is irreducible if and only if for any $\alpha, \beta \in \operatorname{Root}_{f}(L)$ there is $\phi \in \operatorname{Gal}(L / \mathbb{Q})$ such that $\phi(\alpha)=\beta$.

  (ii) Explain how to define an injective homomorphism $\tau: \operatorname{Gal}(L / \mathbb{Q}) \rightarrow S_{n}$. Find an example in which the image of $\tau$ is the subgroup of $S_{3}$ generated by (2 3). Find another example in which $\tau$ is an isomorphism onto $S_{3}$.

  (iii) Let $f(t)=t^{5}-3$ and assume $f$ is irreducible. Find a chain of subgroups of $\operatorname{Gal}(L / \mathbb{Q})$ that shows it is a solvable group. [You may quote without proof any theorems from the course, provided you state them clearly.]

  comment

General Relativity

• Paper 3, Section II, D

  General Relativity | Part II, 2015

  Let $\Gamma_{b c}^{a}$ be the Levi-Civita connection and $R_{b c d}^{a}$ the Riemann tensor corresponding to a metric $g_{a b}(x)$, and let $\widetilde{\Gamma}_{b c}^{a}$ be the Levi-Civita connection and $\widetilde{R}_{b c d}^{a}$ the Riemann tensor corresponding to a metric $\tilde{g}_{a b}(x)$. Let $T_{b c}^{a}=\widetilde{\Gamma}_{b c}^{a}-\Gamma_{b c}^{a}$.

  (a) Show that $T_{b c}^{a}$ is a tensor.

  (b) Using local inertial coordinates for the metric $g_{a b}$, or otherwise, show that

  $$\widetilde{R}_{b c d}^{a}-R_{b c d}^{a}=2 T_{b[d ; c]}^{a}-2 T_{e[d}^{a} T_{c] b}^{e}$$

  holds in all coordinate systems, where the semi-colon denotes covariant differentiation using the connection $\Gamma_{b c}^{a}$. [You may assume that $R_{b c d}^{a}=2 \Gamma_{b[d, c]}^{a}-2 \Gamma_{e[d}^{a} \Gamma_{c] b}^{e}$.]

  (c) In the case that $T_{b c}^{a}=\ell^{a} g_{b c}$ for some vector field $\ell^{a}$, show that $\widetilde{R}_{b d}=R_{b d}$ if and only if

  $$\ell_{b ; d}+\ell_{b} \ell_{d}=0$$

  (d) Using the result that $\ell_{[a ; b]}=0$ if and only if $\ell_{a}=\phi_{, a}$ for some scalar field $\phi$, show that the condition on $\ell_{a}$ in part (c) can be written as

  $$k_{a ; b}=0$$

  for a certain covector field $k_{a}$, which you should define.

  comment

Graph Theory

• Paper 3, Section II, I

  Graph Theory | Part II, 2015

  (a) Let $G$ be a graph. What is a Hamilton cycle in $G$ ? What does it mean to say that $G$ is Hamiltonian?

  (b) Let $G$ be a graph of order $n \geqslant 3$ satisfying $\delta(G) \geqslant \frac{n}{2}$. Show that $G$ is Hamiltonian. For each $n \geqslant 3$, exhibit a non-Hamiltonian graph $G_{n}$ of order $n$ with $\delta\left(G_{n}\right)=\left\lceil\frac{n}{2}\right\rceil-1$.

  (c) Let $H$ be a bipartite graph with $n \geqslant 2$ vertices in each class satisfying $\delta(H)>\frac{n}{2}$. Show that $H$ is Hamiltonian. For each $n \geqslant 2$, exhibit a non-Hamiltonian bipartite graph $H_{n}$ with $n$ vertices in each class and $\delta\left(H_{n}\right)=\left\lfloor\frac{n}{2}\right\rfloor$.

  comment

Integrable Systems

• Paper 3, Section II, D

  Integrable Systems | Part II, 2015

  Let $L=L(t)$ and $A=A(t)$ be real $N \times N$ matrices, with $L$ symmetric and $A$ antisymmetric. Suppose that

  $$\frac{d L}{d t}=L A-A L$$

  Show that all eigenvalues of the matrix $L(t)$ are $t$-independent. Deduce that the coefficients of the polynomial

  $$P(x)=\operatorname{det}(x I-L(t))$$

  are first integrals of the system.

  What does it mean for a $2 n$-dimensional Hamiltonian system to be integrable? Consider the Toda system with coordinates $\left(q_{1}, q_{2}, q_{3}\right)$ obeying

  $$\frac{d^{2} q_{i}}{d t^{2}}=\mathrm{e}^{q_{i-1}-q_{i}}-\mathrm{e}^{q_{i}-q_{i+1}}, \quad i=1,2,3$$

  where here and throughout the subscripts are to be determined modulo 3 so that $q_{4} \equiv q_{1}$ and $q_{0} \equiv q_{3}$. Show that

  $$H\left(q_{i}, p_{i}\right)=\frac{1}{2} \sum_{i=1}^{3} p_{i}^{2}+\sum_{i=1}^{3} \mathrm{e}^{q_{i}-q_{i+1}}$$

  is a Hamiltonian for the Toda system.

  Set $a_{i}=\frac{1}{2} \exp \left(\frac{q_{i}-q_{i+1}}{2}\right)$ and $b_{i}=-\frac{1}{2} p_{i}$. Show that

  $$\frac{d a_{i}}{d t}=\left(b_{i+1}-b_{i}\right) a_{i}, \quad \frac{d b_{i}}{d t}=2\left(a_{i}^{2}-a_{i-1}^{2}\right), \quad i=1,2,3$$

  Is this coordinate transformation canonical?

  By considering the matrices

  $$L=\left(\begin{array}{lll} b_{1} & a_{1} & a_{3} \\ a_{1} & b_{2} & a_{2} \\ a_{3} & a_{2} & b_{3} \end{array}\right), \quad A=\left(\begin{array}{ccc} 0 & -a_{1} & a_{3} \\ a_{1} & 0 & -a_{2} \\ -a_{3} & a_{2} & 0 \end{array}\right)$$

  or otherwise, compute three independent first integrals of the Toda system. [Proof of independence is not required.]

  comment

Linear Analysis

• Paper 3, Section II, G

  Linear Analysis | Part II, 2015

  State and prove the Baire Category Theorem. [Choose any version you like.]

  An isometry from a metric space $(M, d)$ to another metric space $(N, e)$ is a function $\varphi: M \rightarrow N$ such that $e(\varphi(x), \varphi(y))=d(x, y)$ for all $x, y \in M$. Prove that there exists no isometry from the Euclidean plane $\ell_{2}^{2}$ to the Banach space $c_{0}$ of sequences converging to 0 . [Hint: Assume $\varphi: \ell_{2}^{2} \rightarrow \mathrm{c}_{0}$ is an isometry. For $n \in \mathbb{N}$ and $x \in \ell_{2}^{2}$ let $\varphi_{n}(x)$ denote the $n^{\text {th }}$coordinate of $\varphi(x)$. Consider the sets $F_{n}$ consisting of all pairs $(x, y)$ with $\|x\|_{2}=\|y\|_{2}=1$ and $\|\varphi(x)-\varphi(y)\|_{\infty}=\left|\varphi_{n}(x)-\varphi_{n}(y)\right|$.]

  Show that for each $n \in \mathbb{N}$ there is a linear isometry $\ell_{1}^{n} \rightarrow \mathrm{c}_{0}$.

  comment

Logic and Set Theory

• Paper 3, Section II, I

  Logic and Set Theory | Part II, 2015

  (i) State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Where in your proof have you made use of the Axiom of Choice?

  (ii) Let $<$ be a partial ordering on a set $X$. Prove carefully that $<$ may be extended to a total ordering of $X$.

  What does it mean to say that $<$ is well-founded?

  If $<$ has an extension that is a well-ordering, must $<$ be well-founded? If $<$ is well-founded, must every total ordering extending it be a well-ordering? Justify your answers.

  comment

Mathematical Biology

• Paper 3, Section I, E

  Mathematical Biology | Part II, 2015

  The number of a certain type of annual plant in year $n$ is given by $x_{n}$. Each plant produces $k$ seeds that year and then dies before the next year. The proportion of seeds that germinate to produce a new plant the next year is given by $e^{-\gamma x_{n}}$ where $\gamma>0$. Explain briefly why the system can be described by

  $$x_{n+1}=k x_{n} e^{-\gamma x_{n}}$$

  Give conditions on $k$ for a stable positive equilibrium of the plant population size to be possible.

  Winters become milder and now a proportion $s$ of all plants survive each year $(s \in(0,1))$. Assume that plants produce seeds as before while they are alive. Show that a wider range of $k$ now gives a stable positive equilibrium population.

  comment

• Paper 3, Section II, E

  Mathematical Biology | Part II, 2015

  A fungal disease is introduced into an isolated population of frogs. Without disease, the normalised population size $x$ would obey the logistic equation $\dot{x}=x(1-x)$, where the dot denotes differentiation with respect to time. The disease causes death at rate $d$ and there is no recovery. The disease transmission rate is $\beta$ and, in addition, offspring of infected frogs are infected from birth.

  (a) Briefly explain why the population sizes $x$ and $y$ of uninfected and infected frogs respectively now satisfy

  $$\begin{aligned} \dot{x} &=x[1-x-(1+\beta) y] \\ \dot{y} &=y[(1-d)-(1-\beta) x-y] \end{aligned}$$

  (b) The population starts at the disease-free population size $(x=1)$ and a small number of infected frogs are introduced. Show that the disease will successfully invade if and only if $\beta>d$.

  (c) By finding all the equilibria in $x \geqslant 0, y \geqslant 0$ and considering their stability, find the long-term outcome for the frog population. State the relationships between $d$ and $\beta$ that distinguish different final populations.

  (d) Plot the long-term steady total population size as a function of $d$ for fixed $\beta$, and note that an intermediate mortality rate is actually the most harmful. Explain why this is the case.

  comment

Number Theory

• Paper 3, Section I, H

  Number Theory | Part II, 2015

  What does it mean to say that a positive definite binary quadratic form is reduced? Find the three smallest positive integers properly represented by each of the forms $f(x, y)=3 x^{2}+8 x y+9 y^{2}$ and $g(x, y)=15 x^{2}+34 x y+20 y^{2}$. Show that every odd integer represented by some positive definite binary quadratic form with discriminant $-44$ is represented by at least one of the forms $f$ and $g$.

  comment

• Paper 3, Section II, H

  Number Theory | Part II, 2015

  Let $\theta$ be a real number with continued fraction expansion $\left[a_{0}, a_{1}, a_{2}, \ldots\right]$. Define the convergents $p_{n} / q_{n}$ (by means of recurrence relations) and show that for $\beta>0$ we have

  $$\left[a_{0}, a_{1}, \ldots, a_{n-1}, \beta\right]=\frac{\beta p_{n-1}+p_{n-2}}{\beta q_{n-1}+q_{n-2}}$$

  Show that

  $$\left|\theta-\frac{p_{n}}{q_{n}}\right|<\frac{1}{q_{n} q_{n+1}}$$

  and deduce that $p_{n} / q_{n} \rightarrow \theta$ as $n \rightarrow \infty$.

  By computing a suitable continued fraction expansion, find solutions in positive integers $x$ and $y$ to each of the equations $x^{2}-53 y^{2}=4$ and $x^{2}-53 y^{2}=-7$.

  comment

Numerical Analysis

• Paper 3, Section II, E

  Numerical Analysis | Part II, 2015

  (a) Given the finite-difference recurrence

  $$\sum_{k=r}^{s} a_{k} u_{m+k}^{n+1}=\sum_{k=r}^{s} b_{k} u_{m+k}^{n}, \quad m \in \mathbb{Z}, n \in \mathbb{Z}^{+}$$

  that discretises a Cauchy problem, the amplification factor is defined by

  $$H(\theta)=\left(\sum_{k=r}^{s} b_{k} e^{i k \theta}\right) /\left(\sum_{k=r}^{s} a_{k} e^{i k \theta}\right)$$

  Show how $H(\theta)$ acts on the Fourier transform $\hat{u}^{n}$ of $u^{n}$. Hence prove that the method is stable if and only if $|H(\theta)| \leqslant 1$ for all $\theta \in[-\pi, \pi]$.

  (b) The two-dimensional diffusion equation

  $$u_{t}=u_{x x}+c u_{y y}$$

  for some scalar constant $c>0$ is discretised with the forward Euler scheme

  $$u_{i, j}^{n+1}=u_{i, j}^{n}+\mu\left(u_{i+1, j}^{n}-2 u_{i, j}^{n}+u_{i-1, j}^{n}+c u_{i, j+1}^{n}-2 c u_{i, j}^{n}+c u_{i, j-1}^{n}\right)$$

  Using Fourier stability analysis, find the range of values $\mu>0$ for which the scheme is stable.

  comment

Optimization and Control

• Paper 3, Section II, K

  Optimization and Control | Part II, 2015

  A burglar having wealth $x$ may retire, or go burgling another night, in either of towns 1 or 2 . If he burgles in town $i$ then with probability $p_{i}=1-q_{i}$ he will, independently of previous nights, be caught, imprisoned and lose all his wealth. If he is not caught then his wealth increases by 0 or $2 a_{i}$, each with probability $1 / 2$ and independently of what happens on other nights. Values of $p_{i}$ and $a_{i}$ are the same every night. He wishes to maximize his expected wealth at the point he retires, is imprisoned, or $s$ nights have elapsed.

  Using the dynamic programming equation

  $$F_{s}(x)=\max \left\{x, q_{1} E F_{s-1}\left(x+R_{1}\right), q_{2} E F_{s-1}\left(x+R_{2}\right)\right\}$$

  with $R_{j}, F_{0}(x)$ appropriately defined, prove that there exists an optimal policy under which he burgles another night if and only if his wealth is less than $x^{*}=\max _{i}\left\{a_{i} q_{i} / p_{i}\right\}$.

  Suppose $q_{1}>q_{2}$ and $q_{1} a_{1}>q_{2} a_{2}$. Prove that he should never burgle in town 2 .

  [Hint: Suppose $x<x^{*}$, there are $s$ nights to go, and it has been shown that he ought not burgle in town 2 if less than $s$ nights remain. For the case $a_{2}>a_{1}$, separately consider subcases $x+2 a_{2} \geqslant x^{*}$ and $x+2 a_{2}<x^{*}$. An interchange argument may help.]

  comment

Partial Differential Equations

• Paper 3, Section II, E

  Partial Differential Equations | Part II, 2015

  (a) Show that if $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$ is a Schwartz function and $u$ is a tempered distribution which solves

  $$-\Delta u+m^{2} u=f$$

  for some constant $m \neq 0$, then there exists a number $C>0$ which depends only on $m$, such that $\|u\|_{H^{s+2}} \leqslant C\|f\|_{H^{s}}$ for any $s \geqslant 0$. Explain briefly why this inequality remains valid if $f$ is only assumed to be in $H^{s}\left(\mathbb{R}^{n}\right)$.

  Show that if $\epsilon>0$ is given then $\|v\|_{H^{1}}^{2} \leqslant \epsilon\|v\|_{H^{2}}^{2}+\frac{1}{4 \epsilon}\|v\|_{H^{0}}^{2}$ for any $v \in H^{2}\left(\mathbb{R}^{n}\right)$.

  [Hint: The inequality $a \leqslant \epsilon a^{2}+\frac{1}{4 \epsilon}$ holds for any positive $\epsilon$ and $a \in \mathbb{R} .$ ]

  Prove that if $u$ is a smooth bounded function which solves

  $$-\Delta u+m^{2} u=u^{3}+\alpha \cdot \nabla u$$

  for some constant vector $\alpha \in \mathbb{R}^{n}$ and constant $m \neq 0$, then there exists a number $C^{\prime}>0$ such that $\|u\|_{H^{2}} \leqslant C^{\prime}$ and $C^{\prime}$ depends only on $m, \alpha,\|u\|_{L^{\infty}},\|u\|_{L^{2}}$.

  [You may use the fact that, for non-negative $s$, the Sobolev space of functions

  $$\left.H^{s}\left(\mathbb{R}^{n}\right)=\left\{f \in L^{2}\left(\mathbb{R}^{n}\right):\|f\|_{H^{s}}^{2}=\int_{\mathbb{R}^{n}}\left(1+\|\xi\|^{2}\right)^{s}|\hat{f}(\xi)|^{2} d \xi<\infty\right\} .\right]$$

  (b) Let $u(x, t)$ be a smooth real-valued function, which is $2 \pi$-periodic in $x$ and satisfies the equation

  $$u_{t}=u^{2} u_{x x}+u^{3}$$

  Give a complete proof that if $u(x, 0)>0$ for all $x$ then $u(x, t)>0$ for all $x$ and $t>0$.

  comment

Principles of Quantum Mechanics

• Paper 3, Section II, A

  Principles of Quantum Mechanics | Part II, 2015

  Let $|j, m\rangle$ denote the normalised joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, where $\mathbf{J}$ is the angular momentum operator for a quantum system. State clearly the possible values of the quantum numbers $j$ and $m$ and write down the corresponding eigenvalues in units with $\hbar=1$.

  Consider two quantum systems with angular momentum states $\left|\frac{1}{2}, r\right\rangle$ and $|j, m\rangle$. The eigenstates corresponding to their combined angular momentum can be written as

  $$|J, M\rangle=\sum_{r, m} C_{r m}^{J M}\left|\frac{1}{2}, r\right\rangle|j, m\rangle,$$

  where $C_{r m}^{J M}$ are Clebsch-Gordan coefficients for addition of angular momenta $\frac{1}{2}$ and $j$. What are the possible values of $J$ and what is a necessary condition relating $r, m$ and $M$ in order that $C_{r m}^{J M} \neq 0$ ?

  Calculate the values of $C_{r m}^{J M}$ for $j=2$ and for all $M \geqslant \frac{3}{2}$. Use the sign convention that $C_{r m}^{J J}>0$ when $m$ takes its maximum value.

  A particle $X$ with spin $\frac{3}{2}$ and intrinsic parity $\eta_{X}$ is at rest. It decays into two particles $A$ and $B$ with spin $\frac{1}{2}$ and spin 0 , respectively. Both $A$ and $B$ have intrinsic parity $-1$. The relative orbital angular momentum quantum number for the two particle system is $\ell$. What are the possible values of $\ell$ for the cases $\eta_{X}=+1$ and $\eta_{X}=-1$ ?

  Suppose particle $X$ is prepared in the state $\left|\frac{3}{2}, \frac{3}{2}\right\rangle$ before it decays. Calculate the probability $P$ for particle $A$ to be found in the state $\left|\frac{1}{2}, \frac{1}{2}\right\rangle$, given that $\eta_{X}=+1$.

  What is the probability $P$ if instead $\eta_{X}=-1$ ?

  [Units with $\hbar=1$ should be used throughout. You may also use without proof

  $$\left.J_{-}|j, m\rangle=\sqrt{(j+m)(j-m+1)}|j, m-1\rangle .\right]$$

  comment

Principles of Statistics

• Paper 3, Section II, J

  Principles of Statistics | Part II, 2015

  Define what it means for an estimator $\hat{\theta}$ of an unknown parameter $\theta$ to be consistent.

  Let $S_{n}$ be a sequence of random real-valued continuous functions defined on $\mathbb{R}$ such that, as $n \rightarrow \infty, S_{n}(\theta)$ converges to $S(\theta)$ in probability for every $\theta \in \mathbb{R}$, where $S: \mathbb{R} \rightarrow \mathbb{R}$ is non-random. Suppose that for some $\theta_{0} \in \mathbb{R}$ and every $\varepsilon>0$ we have

  $$S\left(\theta_{0}-\varepsilon\right)<0<S\left(\theta_{0}+\varepsilon\right),$$

  and that $S_{n}$ has exactly one zero $\hat{\theta}_{n}$ for every $n \in \mathbb{N}$. Show that $\hat{\theta}_{n} \rightarrow \theta_{0}$ as $n \rightarrow \infty$, and deduce from this that the maximum likelihood estimator (MLE) based on observations $X_{1}, \ldots, X_{n}$ from a $N(\theta, 1), \theta \in \mathbb{R}$ model is consistent.

  Now consider independent observations $\mathbf{X}_{1}, \ldots, \mathbf{X}_{n}$ of bivariate normal random vectors

  $$\mathbf{X}_{i}=\left(X_{1 i}, X_{2 i}\right)^{T} \sim N_{2}\left[\left(\mu_{i}, \mu_{i}\right)^{T}, \sigma^{2} I_{2}\right], \quad i=1, \ldots, n,$$

  where $\mu_{i} \in \mathbb{R}, \sigma>0$ and $I_{2}$ is the $2 \times 2$ identity matrix. Find the MLE $\hat{\mu}=\left(\hat{\mu}_{1}, \ldots, \hat{\mu}_{n}\right)^{T}$ of $\mu=\left(\mu_{1}, \ldots, \mu_{n}\right)^{T}$ and show that the MLE of $\sigma^{2}$ equals

  $$\hat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n} s_{i}^{2}, \quad s_{i}^{2}=\frac{1}{2}\left[\left(X_{1 i}-\hat{\mu}_{i}\right)^{2}+\left(X_{2 i}-\hat{\mu}_{i}\right)^{2}\right]$$

  Show that $\hat{\sigma}^{2}$ is not consistent for estimating $\sigma^{2}$. Explain briefly why the MLE fails in this model.

  [You may use the Law of Large Numbers without proof.]

  comment

Probability and Measure

• Paper 3 , Section II, J

  Probability and Measure | Part II, 2015

  (a) Let $(E, \mathcal{E}, \mu)$ be a measure space. What does it mean to say that $T: E \rightarrow E$ is a measure-preserving transformation? What does it mean to say that a set $A \in \mathcal{E}$ is invariant under $T$ ? Show that the class of invariant sets forms a $\sigma$-algebra.

  (b) Take $E$ to be $[0,1)$ with Lebesgue measure on its Borel $\sigma$-algebra. Show that the baker's map $T:[0,1) \rightarrow[0,1)$ defined by

  $$T(x)=2 x-\lfloor 2 x\rfloor$$

  is measure-preserving.

  (c) Describe in detail the construction of the canonical model for sequences of independent random variables having a given distribution $m$.

  Define the Bernoulli shift map and prove it is a measure-preserving ergodic transformation.

  [You may use without proof other results concerning sequences of independent random variables proved in the course, provided you state these clearly.]

  comment

Representation Theory

• Paper 3, Section II, F

  Representation Theory | Part II, 2015

  (a) State Mackey's theorem, defining carefully all the terms used in the statement.

  (b) Let $G$ be a finite group and suppose that $G$ acts on the set $\Omega$.

  If $n \in \mathbb{N}$, we say that the action of $G$ on $\Omega$ is $n$-transitive if $\Omega$ has at least $n$ elements and for every pair of $n$-tuples $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ such that the $a_{i}$ are distinct elements of $\Omega$ and the $b_{i}$ are distinct elements of $\Omega$, there exists $g \in G$ with $g a_{i}=b_{i}$ for every $i$.

  (i) Let $\Omega$ have at least $n$ elements, where $n \geqslant 1$ and let $\omega \in \Omega$. Show that $G$ acts $n$-transitively on $\Omega$ if and only if $G$ acts transitively on $\Omega$ and the stabiliser $G_{\omega}$ acts $(n-1)$-transitively on $\Omega \backslash\{\omega\}$.

  (ii) Show that the permutation module $\mathbb{C} \Omega$ can be decomposed as

  $$\mathbb{C} \Omega=\mathbb{C}_{G} \oplus V,$$

  where $\mathbb{C}_{G}$ is the trivial module and $V$ is some $\mathbb{C} G$-module.

  (iii) Assume that $|\Omega| \geqslant 2$, so that $V \neq 0$. Prove that $V$ is irreducible if and only if $G$ acts 2-transitively on $\Omega$. In that case show also that $V$ is not the trivial representation. [Hint: Pick any orbit of $G$ on $\Omega$; it is isomorphic as a $G$-set to $G / H$ for some subgroup $H \leqslant G$. Consider the induced character $\left.\operatorname{Ind}_{H}^{G} 1_{H} \cdot\right]$

  comment

Riemann Surfaces

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2015

  Let $\wp(z)$ denote the Weierstrass $\wp$-function with respect to a lattice $\Lambda \subset \mathbb{C}$ and let $f$ be an even elliptic function with periods $\Lambda$. Prove that there exists a rational function $Q$ such that $f(z)=Q(\wp(z))$. If we write $Q(w)=p(w) / q(w)$ where $p$ and $q$ are coprime polynomials, find the degree of $f$ in terms of the degrees of the polynomials $p$ and $q$. Describe all even elliptic functions of degree two. Justify your answers. [You may use standard properties of the Weierstrass $\wp$-function.]

  comment

Statistical Modelling

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2015

  Data are available on the number of counts (atomic disintegration events that take place within a radiation source) recorded with a Geiger counter at a nuclear plant. The counts were registered at each second over a 30 second period for a short-lived, man-made radioactive compound. The first few rows of the dataset are displayed below.

  

  Describe the model being fitted with the following $\mathrm{R}$ command.

  $>$ fit $1<-\operatorname{lm}($ Counts $~$Time, data=geiger)

  Below is a plot against time of the residuals from the model fitted above.

  

  Referring to the plot, suggest how the model could be improved, and write out the $R$ code for fitting this new model. Briefly describe how one could test in $R$ whether the new model is to be preferred over the old model.

  comment

Statistical Physics

• Paper 3, Section II, C

  Statistical Physics | Part II, 2015

  (a) A sample of gas has pressure $p$, volume $V$, temperature $T$ and entropy $S$.

  (i) Use the first law of thermodynamics to derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial p}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{p} .$$

  (ii) Define the heat capacity at constant pressure $C_{p}$ and the enthalpy $H$ and show that $C_{p}=(\partial H / \partial T)_{p}$.

  (b) Consider a perfectly insulated pipe with a throttle valve, as shown.

  

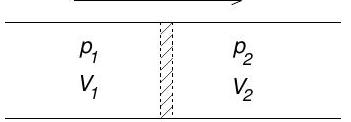
  Gas initially occupying volume $V_{1}$ on the left is forced slowly through the valve at constant pressure $p_{1}$. A constant pressure $p_{2}$ is maintained on the right and the final volume occupied by the gas after passing through the valve is $V_{2}$.

  (i) Show that the enthalpy $H$ of the gas is unchanged by this process.

  (ii) The Joule-Thomson coefficient is defined to be $\mu=(\partial T / \partial p)_{H}$. Show that

  $$\mu=\frac{V}{C_{p}}\left[\frac{T}{V}\left(\frac{\partial V}{\partial T}\right)_{p}-1\right]$$

  [You may assume the identity $(\partial y / \partial x)_{u}=-(\partial u / \partial x)_{y} /(\partial u / \partial y)_{x} \cdot$ ]

  (iii) Suppose that the gas obeys an equation of state

  $$p=k_{B} T\left[\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}\right]$$

  where $N$ is the number of particles. Calculate $\mu$ to first order in $N / V$ and hence derive a condition on $\frac{d}{d T}\left(\frac{B_{2}(T)}{T}\right)$ for obtaining a positive Joule-Thomson coefficient.

  comment

Stochastic Financial Models

• Paper 3, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models | Part II, 2015

  A single-period market consists of $n$ assets whose prices at time $t$ are denoted by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$, and a riskless bank account bearing interest rate $r$. The value of $S_{0}$ is given, and $S_{1} \sim N(\mu, V)$. An investor with utility $U(x)=-\exp (-\gamma x)$ wishes to choose a portfolio of the available assets so as to maximize the expected utility of her wealth at time 1. Find her optimal investment.

  What is the market portfolio for this problem? What is the beta of asset $i$ ? Derive the Capital Asset Pricing Model, that

  Excess return of asset $i=$ Excess return of market portfolio $\times \beta_{i}$.

  The Sharpe ratio of a portfolio $\theta$ is defined to be the excess return of the portfolio $\theta$ divided by the standard deviation of the portfolio $\theta$. If $\rho_{i}$ is the correlation of the return on asset $i$ with the return on the market portfolio, prove that

  Sharpe ratio of asset $i=$ Sharpe ratio of market portfolio $\times \rho_{i}$.

  comment

Topics in Analysis

• Paper 3, Section I, $2 I$

  Topics in Analysis | Part II, 2015

  Let $K$ be a compact subset of $\mathbb{C}$ with path-connected complement. If $w \notin K$ and $\epsilon>0$, show that there is a polynomial $P$ such that

  $$\left|P(z)-\frac{1}{w-z}\right| \leqslant \epsilon$$

  for all $z \in K$.

  comment

• Paper 3, Section II, I

  Topics in Analysis | Part II, 2015

  Let $\alpha>0$. By considering the set $E_{m}$ consisting of those $f \in C([0,1])$ for which there exists an $x \in[0,1]$ with $|f(x+h)-f(x)| \leqslant m|h|^{\alpha}$ for all $x+h \in[0,1]$, or otherwise, give a Baire category proof of the existence of continuous functions $f$ on $[0,1]$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  at each $x \in[0,1]$.

  Are the following statements true? Give reasons.

  (i) There exists an $f \in C([0,1])$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  for each $x \in[0,1]$ and each $\alpha>0$.

  (ii) There exists an $f \in C([0,1])$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  for each $x \in[0,1]$ and each $\alpha \geqslant 0$.

  comment

Waves

• Paper 3, Section II, B

  Waves | Part II, 2015

  Derive the ray-tracing equations for the quantities $\mathrm{d} k_{i} / \mathrm{d} t, \mathrm{~d} \omega / \mathrm{d} t$ and $\mathrm{d} x_{i} / \mathrm{d} t$ during wave propagation through a slowly varying medium with local dispersion relation $\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$, explaining the meaning of the notation $\mathrm{d} / \mathrm{d} t$.

  The dispersion relation for water waves is $\Omega^{2}=g \kappa \tanh (\kappa h)$, where $h$ is the water depth, $\kappa^{2}=k^{2}+l^{2}$, and $k$ and $l$ are the components of $\mathbf{k}$ in the horizontal $x$ and $y$ directions. Water waves are incident from an ocean occupying $x>0,-\infty<y<\infty$ onto a beach at $x=0$. The undisturbed water depth is $h(x)=\alpha x^{p}$, where $\alpha, p$ are positive constants and $\alpha$ is sufficiently small that the depth can be assumed to be slowly varying. Far from the beach, the waves are planar with frequency $\omega_{\infty}$ and with crests making an acute angle $\theta_{\infty}$ with the shoreline.

  Obtain a differential equation (with $k$ defined implicitly) for a ray $y=y(x)$ and show that near the shore the ray satisfies

  $$y-y_{0} \sim A x^{q}$$

  where $A$ and $q$ should be found. Sketch the shape of the wavecrests near the shoreline for the case $p<2$.

  comment