Part II, 2015, Paper 1

Algebraic Geometry

• Paper 1, Section II, F

  Algebraic Geometry | Part II, 2015

  Let $k$ be an algebraically closed field.

  (i) Let $X$ and $Y$ be affine varieties defined over $k$. Given a map $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of affine varieties.

  (ii) With $X, Y$ still affine varieties over $k$, show that there is a one-to-one correspondence between $\operatorname{Hom}(X, Y)$, the set of morphisms between $X$ and $Y$, and $\operatorname{Hom}(A(Y), A(X))$, the set of $k$-algebra homomorphisms between $A(Y)$ and $A(X)$.

  (iii) Let $f: \mathbb{A}^{2} \rightarrow \mathbb{A}^{4}$ be given by $f(t, u)=\left(u, t, t^{2}, t u\right)$. Show that the image of $f$ is an affine variety $X$, and find a set of generators for $I(X)$.

  comment

Algebraic Topology

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2015

  State carefully a version of the Seifert-van Kampen theorem for a cover of a space by two closed sets.

  Let $X$ be the space obtained by gluing together a Möbius band $M$ and a torus $T=S^{1} \times S^{1}$ along a homeomorphism of the boundary of $M$ with $S^{1} \times\{1\} \subset T$. Find a presentation for the fundamental group of $X$, and hence show that it is infinite and non-abelian.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, A

  Applications of Quantum Mechanics | Part II, 2015

  Define the Rayleigh-Ritz quotient $R[\psi]$ for a normalisable state $|\psi\rangle$ of a quantum system with Hamiltonian $H$. Given that the spectrum of $H$ is discrete and that there is a unique ground state of energy $E_{0}$, show that $R[\psi] \geqslant E_{0}$ and that equality holds if and only if $|\psi\rangle$ is the ground state.

  A simple harmonic oscillator (SHO) is a particle of mass $m$ moving in one dimension subject to the potential

  $$V(x)=\frac{1}{2} m \omega^{2} x^{2}$$

  Estimate the ground state energy $E_{0}$ of the SHO by using the ground state wavefunction for a particle in an infinite potential well of width $a$, centred on the origin (the potential is $U(x)=0$ for $|x|<a / 2$ and $U(x)=\infty$ for $|x|>a / 2)$. Take $a$ as the variational parameter.

  Perform a similar estimate for the energy $E_{1}$ of the first excited state of the SHO by using the first excited state of the infinite potential well as a trial wavefunction.

  Is the estimate for $E_{1}$ necessarily an upper bound? Justify your answer.

  $\left[\right.$ You may use : $\int_{-\pi / 2}^{\pi / 2} y^{2} \cos ^{2} y d y=\frac{\pi}{4}\left(\frac{\pi^{2}}{6}-1\right) \quad$ and $\left.\quad \int_{-\pi}^{\pi} y^{2} \sin ^{2} y d y=\pi\left(\frac{\pi^{2}}{3}-\frac{1}{2}\right) \cdot\right]$

  comment

Applied Probability

• Paper 1, Section II, K

  Applied Probability | Part II, 2015

  (a) Give the definition of a birth and death chain in terms of its generator. Show that a measure $\pi$ is invariant for a birth and death chain if and only if it solves the detailed balance equations.

  (b) There are $s$ servers in a post office and a single queue. Customers arrive as a Poisson process of rate $\lambda$ and the service times at each server are independent and exponentially distributed with parameter $\mu$. Let $X_{t}$ denote the number of customers in the post office at time $t$. Find conditions on $\lambda, \mu$ and $s$ for $X$ to be positive recurrent, null recurrent and transient, justifying your answers.

  comment

Asymptotic Methods

• Paper 1, Section II, C

  Asymptotic Methods | Part II, 2015

  (a) State the integral expression for the gamma function $\Gamma(z)$, for $\operatorname{Re}(z)>0$, and express the integral

  $$\int_{0}^{\infty} t^{\gamma-1} e^{i t} d t, \quad 0<\gamma<1$$

  in terms of $\Gamma(\gamma)$. Explain why the constraints on $\gamma$ are necessary.

  (b) Show that

  $$\int_{0}^{\infty} \frac{e^{-k t^{2}}}{\left(t^{2}+t\right)^{\frac{1}{4}}} d t \sim \sum_{m=0}^{\infty} \frac{a_{m}}{k^{\alpha+\beta m}}, \quad k \rightarrow \infty$$

  for some constants $a_{m}, \alpha$ and $\beta$. Determine the constants $\alpha$ and $\beta$, and express $a_{m}$ in terms of the gamma function.

  State without proof the basic result needed for the rigorous justification of the above asymptotic formula.

  [You may use the identity:

  $$\left.(1+z)^{\alpha}=\sum_{m=0}^{\infty} c_{m} z^{m}, \quad c_{m}=\frac{\Gamma(\alpha+1)}{m ! \Gamma(\alpha+1-m)}, \quad|z|<1 .\right]$$

  comment

Classical Dynamics

• Paper 1, Section I, D

  Classical Dynamics | Part II, 2015

  (a) The action for a one-dimensional dynamical system with a generalized coordinate $q$ and Lagrangian $L$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

  State the principle of least action and derive the Euler-Lagrange equation.

  (b) A planar spring-pendulum consists of a light rod of length $l$ and a bead of mass $m$, which is able to slide along the rod without friction and is attached to the ends of the rod by two identical springs of force constant $k$ as shown in the figure. The rod is pivoted at one end and is free to swing in a vertical plane under the influence of gravity.

  

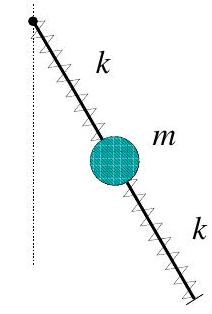
  (i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

  (ii) Derive the equations of motion.

  comment

Coding and Cryptography

• Paper 1, Section I, $3 G$

  Coding and Cryptography | Part II, 2015

  Let $\mathcal{A}$ be a finite alphabet. Explain what is meant by saying that a binary code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ has minimum distance $\delta$. If $c$ is such a binary code with minimum distance $\delta$, show that $c$ is $\delta-1$ error-detecting and $\left\lfloor\frac{1}{2}(\delta-1)\right\rfloor$ error-correcting.

  Show that it is possible to construct a code that has minimum distance $\delta$ for any integer $\delta>0$.

  comment

• Paper 1, Section II, G

  Coding and Cryptography | Part II, 2015

  Define the Hamming code. Show that it is a perfect, linear, 1-error correcting code.

  I wish to send a message through a noisy channel to a friend. The message consists of a large number $N=1,000$ of letters from a 16 -letter alphabet $\mathcal{A}$. When my friend has decoded the message, she can tell whether there have been any errors. If there have, she asks me to send the message again and this is repeated until she has received the message without error. For each individual binary digit that is transmitted, there is independently a small probability $p=0.001$ of an error.

  (a) Suppose that I encode my message by writing each letter as a 4-bit binary string. The whole message is then $4 N$ bits long. What is the probability $P$ that the entire message is transmitted without error? How many times should I expect to transmit the message until my friend receives it without error?

  (b) As an alternative, I use the Hamming code to encode each letter of $\mathcal{A}$ as a 7-bit binary string. What is the probability that my friend can decode a single 7-bit string correctly? Deduce that the probability $Q$ that the entire message is correctly decoded is given approximately by

  $$Q \simeq\left(1-21 p^{2}\right)^{N} \simeq \exp \left(-21 N p^{2}\right)$$

  Which coding method is better?

  comment

Cosmology

• Paper 1, Section I, C

  Cosmology | Part II, 2015

  Consider three galaxies $O, A$ and $B$ with position vectors $\mathbf{r}_{O}, \mathbf{r}_{A}$ and $\mathbf{r}_{B}$ in a homogeneous universe. Assuming they move with non-relativistic velocities $\mathbf{v}_{O}=\mathbf{0}, \mathbf{v}_{A}$ and $\mathbf{v}_{B}$, show that spatial homogeneity implies that the velocity field $\mathbf{v}(\mathbf{r})$ satisfies

  $$\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{A}\right)=\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{O}\right)-\mathbf{v}\left(\mathbf{r}_{A}-\mathbf{r}_{O}\right)$$

  and hence that $\mathbf{v}$ is linearly related to $\mathbf{r}$ by

  $$v_{i}=\sum_{j=1}^{3} H_{i j} r_{j}$$

  where the components of the matrix $H_{i j}$ are independent of $\mathbf{r}$.

  Suppose the matrix $H_{i j}$ has the form

  $$H_{i j}=\frac{D}{t}\left(\begin{array}{ccc} 5 & -1 & -2 \\ 1 & 5 & -1 \\ 2 & 1 & 5 \end{array}\right)$$

  with $D>0$ constant. Describe the kinematics of the cosmological expansion.

  comment

• Paper 1, Section II, C

  Cosmology | Part II, 2015

  A closed universe contains black-body radiation, has a positive cosmological constant $\Lambda$, and is governed by the equation

  $$\frac{\dot{a}^{2}}{a^{2}}=\frac{\Gamma}{a^{4}}-\frac{1}{a^{2}}+\frac{\Lambda}{3},$$

  where $a(t)$ is the scale factor and $\Gamma$ is a positive constant. Using the substitution $y=a^{2}$ and the boundary condition $y(0)=0$, deduce the boundary condition for $\dot{y}(0)$ and show that

  $$\ddot{y}=\frac{4 \Lambda}{3} y-2$$

  and hence that

  $$a^{2}(t)=\frac{3}{2 \Lambda}\left[1-\cosh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)+\lambda \sinh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)\right]$$

  Express the constant $\lambda$ in terms of $\Lambda$ and $\Gamma$.

  Sketch the graphs of $a(t)$ for the cases $\lambda>1$ and $0<\lambda<1$.

  comment

Differential Geometry

• Paper 1, Section II, $22 G$

  Differential Geometry | Part II, 2015

  Let $\Omega \subset \mathbb{R}^{2}$ be a domain (connected open subset) with boundary $\partial \Omega$ a continuously differentiable simple closed curve. Denoting by $A(\Omega)$ the area of $\Omega$ and $l(\partial \Omega)$ the length of the curve $\partial \Omega$, state and prove the isoperimetric inequality relating $A(\Omega)$ and $l(\partial \Omega)$ with optimal constant, including the characterization for equality. [You may appeal to Wirtinger's inequality as long as you state it precisely.]

  Does the result continue to hold if the boundary $\partial \Omega$ is allowed finitely many points at which it is not differentiable? Briefly justify your answer by giving either a counterexample or an indication of a proof.

  comment

Dynamical Systems

• Paper 1, Section II, 28B

  Dynamical Systems | Part II, 2015

  (a) What is a Lyapunov function?

  Consider the dynamical system for $\mathbf{x}(t)=(x(t), y(t))$ given by

  $$\begin{aligned} &\dot{x}=-x+y+x\left(x^{2}+y^{2}\right) \\ &\dot{y}=-y-2 x+y\left(x^{2}+y^{2}\right) \end{aligned}$$

  Prove that the origin is asymptotically stable (quoting carefully any standard results that you use).

  Show that the domain of attraction of the origin includes the region $x^{2}+y^{2}<r_{1}^{2}$ where the maximum possible value of $r_{1}$ is to be determined.

  Show also that there is a region $E=\left\{\mathbf{x} \mid x^{2}+y^{2}>r_{2}^{2}\right\}$ such that $\mathbf{x}(0) \in E$ implies that $|\mathbf{x}(t)|$ increases without bound. Explain your reasoning carefully. Find the smallest possible value of $r_{2}$.

  (b) Now consider the dynamical system

  $$\begin{aligned} \dot{x} &=x-y-x\left(x^{2}+y^{2}\right) \\ \dot{y} &=y+2 x-y\left(x^{2}+y^{2}\right) \end{aligned}$$

  Prove that this system has a periodic solution (again, quoting carefully any standard results that you use).

  Demonstrate that this periodic solution is unique.

  comment

Electrodynamics

• Paper 1, Section II, A

  Electrodynamics | Part II, 2015

  Briefly explain how to interpret the components of the relativistic stress-energy tensor in terms of the density and flux of energy and momentum in some inertial frame.

  (i) The stress-energy tensor of the electromagnetic field is

  $$T_{\mathrm{em}}^{\mu \nu}=\frac{1}{\mu_{0}}\left(F^{\mu \alpha} F_{\alpha}^{\nu}-\frac{1}{4} \eta^{\mu \nu} F^{\alpha \beta} F_{\alpha \beta}\right)$$

  where $F_{\mu \nu}$ is the field strength, $\eta_{\mu \nu}$ is the Minkowski metric, and $\mu_{0}$ is the permeability of free space. Show that $\partial_{\mu} T_{\mathrm{em}}^{\mu \nu}=-F_{\mu}^{\nu} J^{\mu}$, where $J^{\mu}$ is the current 4-vector.

  [ Maxwell's equations are $\partial_{\mu} F^{\mu \nu}=-\mu_{0} J^{\nu}$ and $\partial_{\rho} F_{\mu \nu}+\partial_{\nu} F_{\rho \mu}+\partial_{\mu} F_{\nu \rho}=0 .$ ]

  (ii) A fluid consists of point particles of rest mass $m$ and charge $q$. The fluid can be regarded as a continuum, with 4 -velocity $u^{\mu}(x)$ depending on the position $x$ in spacetime. For each $x$ there is an inertial frame $S_{x}$ in which the fluid particles at $x$ are at rest. By considering components in $S_{x}$, show that the fluid has a current 4-vector field

  $$J^{\mu}=q n_{0} u^{\mu}$$

  and a stress-energy tensor

  $$T_{\text {fluid }}^{\mu \nu}=m n_{0} u^{\mu} u^{\nu},$$

  where $n_{0}(x)$ is the proper number density of particles (the number of particles per unit spatial volume in $S_{x}$ in a small region around $x$ ). Write down the Lorentz 4-force on a fluid particle at $x$. By considering the resulting 4 -acceleration of the fluid, show that the total stress-energy tensor is conserved, i.e.

  $$\partial_{\mu}\left(T_{\mathrm{em}}^{\mu \nu}+T_{\text {fluid }}^{\mu \nu}\right)=0 .$$

  comment

Fluid Dynamics II

• Paper 1, Section II, E

  Fluid Dynamics II | Part II, 2015

  (i) In a Newtonian fluid, the deviatoric stress tensor is linearly related to the velocity gradient so that the total stress tensor is

  $$\sigma_{i j}=-p \delta_{i j}+A_{i j k l} \frac{\partial u_{k}}{\partial x_{l}}$$

  Show that for an incompressible isotropic fluid with a symmetric stress tensor we necessarily have

  $$A_{i j k l} \frac{\partial u_{k}}{\partial x_{l}}=2 \mu e_{i j} \text {, }$$

  where $\mu$ is a constant which we call the dynamic viscosity and $e_{i j}$ is the symmetric part of $\partial u_{i} / \partial x_{j}$.

  (ii) Consider Stokes flow due to the translation of a rigid sphere $S_{a}$ of radius $a$ so that the sphere exerts a force $\mathbf{F}$ on the fluid. At distances much larger than the radius of the sphere, the instantaneous velocity and pressure fields are

  $$u_{i}(\mathbf{x})=\frac{1}{8 \mu \pi}\left(\frac{F_{i}}{r}+\frac{F_{m} x_{m} x_{i}}{r^{3}}\right), \quad p(\mathbf{x})=\frac{1}{4 \pi} \frac{F_{m} x_{m}}{r^{3}},$$

  where $\mathbf{x}$ is measured with respect to an origin located at the centre of the sphere, and $r=|\mathbf{x}|$.

  Consider a sphere $S_{R}$ of radius $R \gg a$ instantaneously concentric with $S_{a}$. By explicitly computing the tractions and integrating them, show that the force $G$ exerted by the fluid located in $r>R$ on $S_{R}$ is constant and independent of $R$, and evaluate it.

  (iii) Explain why the Stokes equations in the absence of body forces can be written

  $$\frac{\partial \sigma_{i j}}{\partial x_{j}}=0$$

  Show that by integrating this equation in the fluid volume located instantaneously between $S_{a}$ and $S_{R}$, you can recover the result in (ii) directly.

  comment

Further Complex Methods

• Paper 1, Section $I$, B

  Further Complex Methods | Part II, 2015

  Evaluate the real integral

  $$\int_{0}^{\infty} \frac{x^{1 / 2} \ln x}{1+x^{2}} d x$$

  where $x^{1 / 2}$ is taken to be the positive square root.

  What is the value of

  $$\int_{0}^{\infty} \frac{x^{1 / 2}}{1+x^{2}} d x ?$$

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2015

  Consider the differential equation

  $$x y^{\prime \prime}+(a-x) y^{\prime}-b y=0$$

  where $a$ and $b$ are constants with $\operatorname{Re}(b)>0$ and $\operatorname{Re}(a-b)>0$. Laplace's method for finding solutions involves writing

  $$y(x)=\int_{C} e^{x t} f(t) d t$$

  for some suitable contour $C$ and some suitable function $f(t)$. Determine $f(t)$ for the equation $(*)$ and use a clearly labelled diagram to specify contours $C$ giving two independent solutions when $x$ is real in each of the cases $x>0$ and $x<0$.

  Now let $a=3$ and $b=1$. Find explicit expressions for two independent solutions to $(*)$. Find, in addition, a solution $y(x)$ with $y(0)=1$.

  comment

Galois Theory

• Paper 1, Section II, $17 \mathrm{~F}$

  Galois Theory | Part II, 2015

  (i) Let $K \subseteq L$ be a field extension and $f \in K[t]$ be irreducible of positive degree. Prove the theorem which states that there is a $1-1$ correspondence

  $$\operatorname{Root}_{f}(L) \longleftrightarrow \operatorname{Hom}_{K}\left(\frac{K[t]}{\langle f\rangle}, L\right)$$

  (ii) Let $K$ be a field and $f \in K[t]$. What is a splitting field for $f$ ? What does it mean to say $f$ is separable? Show that every $f \in K[t]$ is separable if $K$ is a finite field.

  (iii) The primitive element theorem states that if $K \subseteq L$ is a finite separable field extension, then $L=K(\alpha)$ for some $\alpha \in L$. Give the proof of this theorem assuming $K$ is infinite.

  comment

General Relativity

• Paper 1, Section II, 35D

  General Relativity | Part II, 2015

  A vector field $\xi^{a}$ is said to be a conformal Killing vector field of the metric $g_{a b}$ if

  $$\xi_{(a ; b)}=\frac{1}{2} \psi g_{a b}$$

  for some scalar field $\psi$. It is a Killing vector field if $\psi=0$.

  (a) Show that $(*)$ is equivalent to

  $$\xi^{c} g_{a b, c}+\xi_{, a}^{c} g_{b c}+\xi_{, b}^{c} g_{a c}=\psi g_{a b}$$

  (b) Show that if $\xi^{a}$ is a conformal Killing vector field of the metric $g_{a b}$, then $\xi^{a}$ is a Killing vector field of the metric $\mathrm{e}^{2 \phi} g_{a b}$, where $\phi$ is any function that obeys

  $$2 \xi^{c} \phi_{, c}+\psi=0 .$$

  (c) Use part (b) to find an example of a metric with coordinates $t, x, y$ and $z$ (where $t>0)$ for which $(t, x, y, z)$ are the contravariant components of a Killing vector field. [Hint: You may wish to start by considering what happens in Minkowski space.]

  comment

Graph Theory

• Paper 1, Section II, I

  Graph Theory | Part II, 2015

  (a) What does it mean to say that a graph $G$ is strongly regular with parameters $(k, a, b) ?$

  (b) Let $G$ be an incomplete, strongly regular graph with parameters $(k, a, b)$ and of order $n$. Suppose $b \geqslant 1$. Show that the numbers

  $$\frac{1}{2}\left(n-1 \pm \frac{(n-1)(b-a)-2 k}{\sqrt{(a-b)^{2}+4(k-b)}}\right)$$

  are integers.

  (c) Suppose now that $G$ is an incomplete, strongly regular graph with parameters $(k, 0,3)$. Show that $|G| \in\{6,162\}$.

  comment

Integrable Systems

• Paper 1, Section II, D

  Integrable Systems | Part II, 2015

  Let $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ be an evolution equation for the function $u=u(x, t)$. Assume $u$ and all its derivatives decay rapidly as $|x| \rightarrow \infty$. What does it mean to say that the evolution equation for $u$ can be written in Hamiltonian form?

  The modified KdV (mKdV) equation for $u$ is

  $$u_{t}+u_{x x x}-6 u^{2} u_{x}=0 .$$

  Show that small amplitude solutions to this equation are dispersive.

  Demonstrate that the mKdV equation can be written in Hamiltonian form and define the associated Poisson bracket $\{,$,} on the space of functionals of u. Verify that the Poisson bracket is linear in each argument and anti-symmetric.

  Show that a functional $I=I[u]$ is a first integral of the mKdV equation if and only if $\{I, H\}=0$, where $H=H[u]$ is the Hamiltonian.

  Show that if $u$ satisfies the mKdV equation then

  $$\frac{\partial}{\partial t}\left(u^{2}\right)+\frac{\partial}{\partial x}\left(2 u u_{x x}-u_{x}^{2}-3 u^{4}\right)=0$$

  Using this equation, show that the functional

  $$I[u]=\int u^{2} d x$$

  Poisson-commutes with the Hamiltonian.

  comment

Linear Analysis

• Paper 1, Section II, G

  Linear Analysis | Part II, 2015

  (a) Let $\left(e_{n}\right)_{n=1}^{\infty}$ be an orthonormal basis of an inner product space $X$. Show that for all $x \in X$ there is a unique sequence $\left(a_{n}\right)_{n=1}^{\infty}$ of scalars such that $x=\sum_{n=1}^{\infty} a_{n} e_{n}$.

  Assume now that $X$ is a Hilbert space and that $\left(f_{n}\right)_{n=1}^{\infty}$ is another orthonormal basis of $X$. Prove that there is a unique bounded linear map $U: X \rightarrow X$ such that $U\left(e_{n}\right)=f_{n}$ for all $n \in \mathbb{N}$. Prove that this map $U$ is unitary.

  (b) Let $1 \leqslant p<\infty$ with $p \neq 2$. Show that no subspace of $\ell_{2}$ is isomorphic to $\ell_{p}$. [Hint: Apply the generalized parallelogram law to suitable vectors.]

  comment

Logic and Set Theory

• Paper 1, Section II, I

  Logic and Set Theory | Part II, 2015

  State and prove the Completeness Theorem for Propositional Logic.

  [You do not need to give definitions of the various terms involved. You may assume the Deduction Theorem, provided that you state it precisely.]

  State the Compactness Theorem and the Decidability Theorem, and deduce them from the Completeness Theorem.

  Let $S$ consist of the propositions $p_{n+1} \Rightarrow p_{n}$ for $n=1,2,3, \ldots$. Does $S$ prove $p_{1}$ ? Justify your answer. [Here $p_{1}, p_{2}, p_{3}, \ldots$ are primitive propositions.]

  comment

Mathematical Biology

• Paper 1, Section I, E

  Mathematical Biology | Part II, 2015

  The population density $n(a, t)$ of individuals of age $a$ at time $t$ satisfies

  $$\frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=-\mu(a) n(a, t), \quad n(0, t)=\int_{0}^{\infty} b(a) n(a, t) d a$$

  where $\mu(a)$ is the age-dependent death rate and $b(a)$ is the birth rate per individual of age $a$. Show that this may be solved with a similarity solution of the form $n(a, t)=e^{\gamma t} r(a)$ if the growth rate $\gamma$ satisfies $\phi(\gamma)=1$ where

  $$\phi(\gamma)=\int_{0}^{\infty} b(a) e^{-\gamma a-\int_{0}^{a} \mu(s) d s} d a$$

  Suppose now that the birth rate is given by $b(a)=B a^{p} e^{-\lambda a}$ with $B, \lambda>0$ and $p$ is a positive integer, and the death rate is constant in age (i.e. $\mu(a)=\mu)$. Find the average number of offspring per individual.

  Find the similarity solution, and find the threshold $B^{*}$ for the birth parameter $B$ so that $B>B^{*}$ corresponds to a growing population.

  comment

Number Fields

• Paper 1, Section II, $16 \mathrm{H}$

  Number Fields | Part II, 2015

  (a) Let $K$ be a number field, and $f$ a monic polynomial whose coefficients are in $\mathcal{O}_{K}$. Let $M$ be a field containing $K$ and $\alpha \in M$. Show that if $f(\alpha)=0$, then $\alpha$ is an algebraic integer.

  Hence conclude that if $h \in K[x]$ is monic, with $h^{n} \in \mathcal{O}_{K}[x]$, then $h \in \mathcal{O}_{K}[x]$.

  (b) Compute an integral basis for $\mathcal{O}_{\mathbb{Q}(\alpha)}$ when the minimum polynomial of $\alpha$ is $x^{3}-x-4$.

  comment

Number Theory

• Paper 1, Section I, H

  Number Theory | Part II, 2015

  Define the Legendre symbol $\left(\frac{a}{p}\right)$. State and prove Euler's criterion, assuming if you wish the existence of primitive roots $\bmod p$.

  By considering the prime factors of $n^{2}+4$ for $n$ an odd integer, prove that there are infinitely many primes $p$ with $p \equiv 5(\bmod 8)$.

  comment

Numerical Analysis

• Paper 1, Section II, 38E

  Numerical Analysis | Part II, 2015

  (a) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left(a(x) \frac{\partial u}{\partial x}\right) \quad \text { in } \quad 0 \leqslant x \leqslant 1, \quad t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x)$ in $0 \leqslant x \leqslant 1$ and zero boundary conditions at $x=0$ and $x=1$, is solved by the finite-difference method

  $$\begin{array}{r} u_{m}^{n+1}=u_{m}^{n}+\mu\left[a_{m-\frac{1}{2}} u_{m-1}^{n}-\left(a_{m-\frac{1}{2}}+a_{m+\frac{1}{2}}\right) u_{m}^{n}+a_{m+\frac{1}{2}} u_{m+1}^{n}\right] \\ m=1,2, \ldots, M \end{array}$$

  where $\mu=k / h^{2}, k=\Delta t, h=1 /(M+1), u_{m}^{n} \approx u(m h, n k)$, and $a_{\alpha}=a(\alpha h)$.

  Assuming that the function $a$ and the exact solution are sufficiently smooth, prove that the exact solution satisfies the numerical scheme with error $O\left(h^{3}\right)$ for constant $\mu$.

  (b) For the problem in part (a), assume that there exist $0<a_{-}<a_{+}<\infty$ such that $a_{-} \leqslant a(x) \leqslant a_{+}$for all $0 \leqslant x \leqslant 1$. State (without proof) the Gershgorin theorem and prove that the method is stable for $0<\mu \leqslant 1 /\left(2 a_{+}\right)$.

  comment

Partial Differential Equations

• Paper 1, Section II, E

  Partial Differential Equations | Part II, 2015

  (a) State the Cauchy-Kovalevskaya theorem, and explain for which values of $a \in \mathbb{R}$ it implies the existence of solutions to the Cauchy problem

  $$x u_{x}+y u_{y}+a u_{z}=u, \quad u(x, y, 0)=f(x, y),$$

  where $f$ is real analytic. Using the method of characteristics, solve this problem for these values of $a$, and comment on the behaviour of the characteristics as $a$ approaches any value where the non-characteristic condition fails.

  (b) Consider the Cauchy problem

  $$u_{y}=v_{x}, \quad v_{y}=-u_{x}$$

  with initial data $u(x, 0)=f(x)$ and $v(x, 0)=0$ which are $2 \pi$-periodic in $x$. Give an example of a sequence of smooth solutions $\left(u_{n}, v_{n}\right)$ which are also $2 \pi$-periodic in $x$ whose corresponding initial data $u_{n}(x, 0)=f_{n}(x)$ and $v_{n}(x, 0)=0$ are such that $\int_{0}^{2 \pi}\left|f_{n}(x)\right|^{2} d x \rightarrow 0$ while $\int_{0}^{2 \pi}\left|u_{n}(x, y)\right|^{2} d x \rightarrow \infty$ for non-zero $y$ as $n \rightarrow \infty$

  Comment on the significance of this in relation to the concept of well-posedness.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, A

  Principles of Quantum Mechanics | Part II, 2015

  If $A$ and $B$ are operators which each commute with their commutator $[A, B]$, show that

  $$F(\lambda)=e^{\lambda A} e^{\lambda B} e^{-\lambda(A+B)} \quad \text { satisfies } \quad F^{\prime}(\lambda)=\lambda[A, B] F(\lambda)$$

  By solving this differential equation for $F(\lambda)$, deduce that

  $$e^{A} e^{B}=e^{\frac{1}{2}[A, B]} e^{A+B}$$

  The annihilation and creation operators for a harmonic oscillator of mass $m$ and frequency $\omega$ are defined by

  $$a=\sqrt{\frac{m \omega}{2 \hbar}}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\sqrt{\frac{m \omega}{2 \hbar}}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  Write down an expression for the general normalised eigenstate $|n\rangle(n=0,1,2, \ldots)$ of the oscillator Hamiltonian $H$ in terms of the ground state $|0\rangle$. What is the energy eigenvalue $E_{n}$ of the state $|n\rangle ?$

  Suppose the oscillator is now subject to a small perturbation so that it is described by the modified Hamiltonian $H+\varepsilon V(\hat{x})$ with $V(\hat{x})=\cos (\mu \hat{x})$. Show that

  $$V(\hat{x})=\frac{1}{2} e^{-\gamma^{2} / 2}\left(e^{i \gamma a^{\dagger}} e^{i \gamma a}+e^{-i \gamma a^{\dagger}} e^{-i \gamma a}\right)$$

  where $\gamma$ is a constant, to be determined. Hence show that to $O\left(\varepsilon^{2}\right)$ the shift in the ground state energy as a result of the perturbation is

  $$\varepsilon e^{-\mu^{2} \hbar / 4 m \omega}-\varepsilon^{2} e^{-\mu^{2} \hbar / 2 m \omega} \frac{1}{\hbar \omega} \sum_{p=1}^{\infty} \frac{1}{(2 p) ! 2 p}\left(\frac{\mu^{2} \hbar}{2 m \omega}\right)^{2 p} .$$

  [Standard results of perturbation theory may be quoted without proof.]

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2015

  Consider a normally distributed random vector $X \in \mathbb{R}^{p}$ modelled as $X \sim N\left(\theta, I_{p}\right)$ where $\theta \in \mathbb{R}^{p}, I_{p}$ is the $p \times p$ identity matrix, and where $p \geqslant 3$. Define the Stein estimator $\hat{\theta}_{S T E I N}$ of $\theta$.

  Prove that $\hat{\theta}_{S T E I N}$ dominates the estimator $\tilde{\theta}=X$ for the risk function induced by quadratic loss

  $$\ell(a, \theta)=\sum_{i=1}^{p}\left(a_{i}-\theta_{i}\right)^{2}, \quad a \in \mathbb{R}^{p}$$

  Show however that the worst case risks coincide, that is, show that

  $$\sup _{\theta \in \mathbb{R}^{p}} E_{\theta} \ell(X, \theta)=\sup _{\theta \in \mathbb{R}^{p}} E_{\theta} \ell\left(\hat{\theta}_{S T E I N}, \theta\right)$$

  [You may use Stein's lemma without proof, provided it is clearly stated.]

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2015

  (a) Define the following concepts: a $\pi$-system, a $d$-system and a $\sigma$-algebra.

  (b) State the Dominated Convergence Theorem.

  (c) Does the set function

  $$\mu(A)= \begin{cases}0 & \text { for } A \text { bounded } \\ 1 & \text { for } A \text { unbounded }\end{cases}$$

  furnish an example of a Borel measure?

  (d) Suppose $g:[0,1] \rightarrow[0,1]$ is a measurable function. Let $f:[0,1] \rightarrow \mathbb{R}$ be continuous with $f(0) \leqslant f(1)$. Show that the limit

  $$\lim _{n \rightarrow \infty} \int_{0}^{1} f\left(g(x)^{n}\right) d x$$

  exists and lies in the interval $[f(0), f(1)]$

  comment

Representation Theory

• Paper 1, Section II, F

  Representation Theory | Part II, 2015

  (a) Let $G$ be a finite group and let $\rho: G \rightarrow \mathrm{GL}_{2}(\mathbb{C})$ be a representation of $G$. Suppose that there are elements $g, h$ in $G$ such that the matrices $\rho(g)$ and $\rho(h)$ do not commute. Use Maschke's theorem to prove that $\rho$ is irreducible.

  (b) Let $n$ be a positive integer. You are given that the dicyclic group

  $$G_{4 n}=\left\langle a, b: a^{2 n}=1, a^{n}=b^{2}, b^{-1} a b=a^{-1}\right\rangle$$

  has order $4 n$.

  (i) Show that if $\epsilon$ is any $(2 n)$ th root of unity in $\mathbb{C}$, then there is a representation of $G_{4 n}$ over $\mathbb{C}$ which sends

  $$a \mapsto\left(\begin{array}{cc} \epsilon & 0 \\ 0 & \epsilon^{-1} \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} 0 & 1 \\ \epsilon^{n} & 0 \end{array}\right)$$

  (ii) Find all the irreducible representations of $G_{4 n}$.

  (iii) Find the character table of $G_{4 n}$.

  [Hint: You may find it helpful to consider the cases $n$ odd and $n$ even separately.]

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2015

  Let $f: R \rightarrow S$ be a non-constant holomorphic map between compact connected Riemann surfaces and let $B \subset S$ denote the set of branch points. Show that the map $f: R \backslash f^{-1}(B) \rightarrow S \backslash B$ is a regular covering map.

  Given $w \in S \backslash B$ and a closed curve $\gamma$ in $S \backslash B$ with initial and final point $w$, explain how this defines a permutation of the (finite) set $f^{-1}(w)$. Show that the group $H$ obtained from all such closed curves is a transitive subgroup of the full symmetric group of the fibre $f^{-1}(w)$.

  Find the group $H$ for $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ where $f(z)=z^{3} /\left(1-z^{2}\right)$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2015

  The outputs $Y_{1}, \ldots, Y_{n}$ of a particular process are positive and are believed to be related to $p$-vectors of covariates $x_{1}, \ldots, x_{n}$ according to the following model

  $$\log \left(Y_{i}\right)=\mu+x_{i}^{T} \beta+\varepsilon_{i}$$

  In this model $\varepsilon_{i}$ are i.i.d. $N\left(0, \sigma^{2}\right)$ random variables where $\sigma>0$ is known. It is not possible to measure the output directly, but we can detect whether the output is greater than or less than or equal to a certain known value $c>0$. If

  $$Z_{i}= \begin{cases}1 & \text { if } Y_{i}>c \\ 0 & \text { if } Y_{i} \leqslant c\end{cases}$$

  show that a probit regression model can be used for the data $\left(Z_{i}, x_{i}\right), i=1, \ldots, n$.

  How can we recover $\mu$ and $\beta$ from the parameters of the probit regression model?

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2015

  An experiment is conducted where scientists count the numbers of each of three different strains of fleas that are reproducing in a controlled environment. Varying concentrations of a particular toxin that impairs reproduction are administered to the fleas. The results of the experiment are stored in a data frame $f l e a s$ in $\mathrm{R}$, whose first few rows are given below.

  

  The full dataset has 80 rows. The first column provides the number of fleas, the second provides the concentration of the toxin and the third specifies the strain of the flea as factors 0,1 or 2 . Strain 0 is the common flea and strains 1 and 2 have been genetically modified in a way thought to increase their ability to reproduce in the presence of the toxin.

  Explain and interpret the $\mathrm{R}$ commands and (abbreviated) output below. In particular, you should describe the model being fitted, briefly explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary.

  

  Explain and motivate the following $\mathrm{R}$ code in the light of the output above. Briefly explain the differences between the models fitted below, and the model corresponding to $f$ it $1 .$

  

  Denote by $M_{1}, M_{2}, M_{3}$ the three models being fitted in sequence above. Explain the hypothesis tests comparing the models to each other that can be performed using the output from the following $R$ code.

  $>c($ fit1$dev, fit2$dev, fit3$dev)

  [1] $56.8756 .9376 .98$

  $>\operatorname{qchisq}(0.95, \mathrm{df}=1)$

  [1] $3.84$

  Use these numbers to comment on the most appropriate model for the data.

  comment

Statistical Physics

• Paper 1, Section II, C

  Statistical Physics | Part II, 2015

  (a) Define the canonical partition function $Z$ for a system with energy levels $E_{n}$, where $n$ labels states, given that the system is in contact with a heat reservoir at temperature $T$. What is the probability $p(n)$ that the system occupies state $n$ ? Starting from an expression for the entropy $S=k_{B} \partial(T \ln Z) / \partial T$, deduce that

  $$S=-k_{B} \sum_{n} p(n) \ln p(n)$$

  (b) Consider an ensemble consisting of $W$ copies of the system in part (a) with $W$ very large, so that there are $W p(n)$ members of the ensemble in state $n$. Starting from an expression for the number of ways in which this can occur, find the entropy $S_{W}$ of the ensemble and hence re-derive the expression $(*)$. [You may assume Stirling's formula $\ln X ! \approx X \ln X-X$ for $X$ large. $]$

  (c) Consider a system of $N$ non-interacting particles at temperature $T$. Each particle has $q$ internal states with energies

  $$0, \mathcal{E}, 2 \mathcal{E}, \ldots,(q-1) \mathcal{E}$$

  Assuming that the internal states are the only relevant degrees of freedom, calculate the total entropy of the system. Find the limiting values of the entropy as $T \rightarrow 0$ and $T \rightarrow \infty$ and comment briefly on your answers.

  comment

Stochastic Financial Models

• Paper 1, Section II, $26 K$

  Stochastic Financial Models | Part II, 2015

  (i) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (ii) If $Y$ is an integrable random variable and $Y_{n}=E\left[Y \mid \mathcal{F}_{n}\right]$, prove that $\left(Y_{n}, \mathcal{F}_{n}\right)$ is a martingale. [Standard facts about conditional expectation may be used without proof provided they are clearly stated.] When is it the case that the limit $\lim _{n \rightarrow \infty} Y_{n}$ exists almost surely?

  (iii) An urn contains initially one red ball and one blue ball. A ball is drawn at random and then returned to the urn with a new ball of the other colour. This process is repeated, adding one ball at each stage to the urn. If the number of red balls after $n$ draws and replacements is $X_{n}$, and the number of blue balls is $Y_{n}$, show that $M_{n}=h\left(X_{n}, Y_{n}\right)$ is a martingale, where

  $$h(x, y)=(x-y)(x+y-1)$$

  Does this martingale converge almost surely?

  comment

Topics in Analysis

• Paper 1, Section I, I

  Topics in Analysis | Part II, 2015

  Let $\Omega$ be a non-empty bounded open subset of $\mathbb{R}^{2}$ with closure $\bar{\Omega}$ and boundary $\partial \Omega$. Let $\phi: \bar{\Omega} \rightarrow \mathbb{R}$ be continuous with $\phi$ twice differentiable on $\Omega$.

  (i) Why does $\phi$ have a maximum on $\bar{\Omega}$ ?

  (ii) If $\epsilon>0$ and $\nabla^{2} \phi \geqslant \epsilon$ on $\Omega$, show that $\phi$ has a maximum on $\partial \Omega$.

  (iii) If $\nabla^{2} \phi \geqslant 0$ on $\Omega$, show that $\phi$ has a maximum on $\partial \Omega$.

  (iv) If $\nabla^{2} \phi=0$ on $\Omega$ and $\phi=0$ on $\partial \Omega$, show that $\phi=0$ on $\bar{\Omega}$.

  comment

Waves

• Paper 1, Section II, 37B

  Waves | Part II, 2015

  An acoustic plane wave (not necessarily harmonic) travels at speed $c_{0}$ in the direction $\hat{\mathbf{k}}$, where $|\hat{\mathbf{k}}|=1$, through an inviscid, compressible fluid of unperturbed density $\rho_{0}$. Show that the velocity $\tilde{\mathbf{u}}$ is proportional to the perturbation pressure $\tilde{p}$, and find $\tilde{\mathbf{u}} / \tilde{p}$. Define the acoustic intensity $\mathbf{I}$.

  A harmonic acoustic plane wave with wavevector $\mathbf{k}=k(\cos \theta, \sin \theta, 0)$ and unitamplitude perturbation pressure is incident from $x<0$ on a thin elastic membrane at unperturbed position $x=0$. The regions $x<0$ and $x>0$ are both occupied by gas with density $\rho_{0}$ and sound speed $c_{0}$. The kinematic boundary conditions at the membrane are those appropriate for an inviscid fluid, and the (linearized) dynamic boundary condition

  $$m \frac{\partial^{2} X}{\partial t^{2}}-T \frac{\partial^{2} X}{\partial y^{2}}+[\tilde{p}(0, y, t)]_{-}^{+}=0$$

  where $T$ and $m$ are the tension and mass per unit area of the membrane, and $x=X(y, t)$ (with $|k X| \ll 1$ ) is its perturbed position. Find the amplitudes of the reflected and transmitted pressure perturbations, expressing your answers in terms of the dimensionless parameter

  $$\alpha=\frac{\rho_{0} c_{0}^{2}}{k \cos \theta\left(m c_{0}^{2}-T \sin ^{2} \theta\right)} .$$

  Hence show that the time-averaged energy flux in the $x$-direction is conserved across the membrane.

  comment