Explain how the Papperitz symbol

$$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha_{1} & \beta_{1} & \gamma_{1} & z \\ \alpha_{2} & \beta_{2} & \gamma_{2} & \end{array}\right\}$$

represents a differential equation with certain properties. [You need not write down the differential equation explicitly.]

The hypergeometric function $F(a, b, c ; z)$ is defined to be the solution of the equation given by the Papperitz symbol

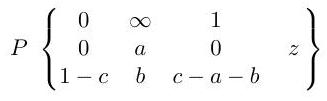
that is analytic at $z=0$ and such that $F(a, b, c ; 0)=1$. Show that

$$F(a, b, c ; z)=(1-z)^{-a} F\left(a, c-b, c ; \frac{z}{z-1}\right) \text {, }$$

indicating clearly any general results for manipulating Papperitz symbols that you use.