(a) The action for a one-dimensional dynamical system with a generalized coordinate $q$ and Lagrangian $L$ is given by

$$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

State the principle of least action and derive the Euler-Lagrange equation.

(b) A planar spring-pendulum consists of a light rod of length $l$ and a bead of mass $m$, which is able to slide along the rod without friction and is attached to the ends of the rod by two identical springs of force constant $k$ as shown in the figure. The rod is pivoted at one end and is free to swing in a vertical plane under the influence of gravity.

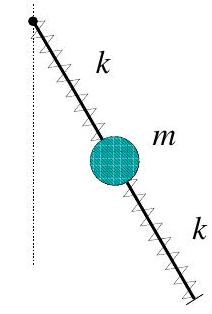
(i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

(ii) Derive the equations of motion.