Part II, 2013, Paper 4

Algebraic Geometry

• Paper 4, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $C$ be a nonsingular projective curve, and $D$ a divisor on $C$ of degree $d$.

  (i) State the Riemann-Roch theorem for $D$, giving a brief explanation of each term. Deduce that if $d>2 g-2$ then $\ell(D)=1-g+d$.

  (ii) Show that, for every $P \in C$,

  $$\ell(D-P) \geqslant \ell(D)-1$$

  Deduce that $\ell(D) \leqslant 1+d$. Show also that if $\ell(D)>1$, then $\ell(D-P)=\ell(D)-1$ for all but finitely many $P \in C$.

  (iii) Deduce that for every $d \geqslant g-1$ there exists a divisor $D$ of degree $d$ with $\ell(D)=1-g+d$.

  comment

Algebraic Topology

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Lefschetz fixed point theorem.

  (ii) Show that if $n$ is even, then for every map $f: S^{n} \rightarrow S^{n}$ there is a point $x \in S^{n}$ such that $f(x)=\pm x$. Is this true if $n$ is odd? [Standard results on the homology groups for the $n$-sphere may be assumed without proof, provided they are stated clearly.]

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  Define the Floquet matrix for a particle moving in a periodic potential in one dimension and explain how it determines the allowed energy bands of the system.

  A potential barrier in one dimension has the form

  $$V(x)= \begin{cases}V_{0}(x), & |x|<a / 4 \\ 0, & |x|>a / 4\end{cases}$$

  where $V_{0}(x)$ is a smooth, positive function of $x$. The reflection and transmission amplitudes for a particle of wavenumber $k>0$, incident from the left, are $r(k)$ and $t(k)$ respectively. For a particle of wavenumber $-k$, incident from the right, the corresponding amplitudes are $r^{\prime}(k)$ and $t^{\prime}(k)=t(k)$. In the following, for brevity, we will suppress the $k$-dependence of these quantities.

  Consider the periodic potential $\tilde{V}$, defined by $\tilde{V}(x)=V(x)$ for $|x|<a / 2$ and by $\tilde{V}(x+a)=\widetilde{V}(x)$ elsewhere. Write down two linearly independent solutions of the corresponding Schrödinger equation in the region $-3 a / 4<x<-a / 4$. Using the scattering data given above, extend these solutions to the region $a / 4<x<3 a / 4$. Hence find the Floquet matrix of the system in terms of the amplitudes $r, r^{\prime}$ and $t$ defined above.

  Show that the edges of the allowed energy bands for this potential lie at $E=\hbar^{2} k^{2} / 2 m$, where

  $$k a=i \log \left(t \pm \sqrt{r r^{\prime}}\right)$$

  comment

Applied Probability

• Paper 4, Section II, J

  Applied Probability | Part II, 2013

  (i) Define an $M / M / 1$ queue. Justifying briefly your answer, specify when this queue has a stationary distribution, and identify that distribution. State and prove Burke's theorem for this queue.

  (ii) Let $\left(L_{1}(t), \ldots, L_{N}(t), t \geqslant 0\right)$ denote a Jackson network of $N$ queues, where the entrance and service rates for queue $i$ are respectively $\lambda_{i}$ and $\mu_{i}$, and each customer leaving queue $i$ moves to queue $j$ with probability $p_{i j}$ after service. We assume $\sum_{j} p_{i j}<1$ for each $i=1, \ldots, N$; with probability $1-\sum_{j} p_{i j}$ a customer leaving queue $i$ departs from the system. State Jackson's theorem for this network. [You are not required to prove it.] Are the processes $\left(L_{1}(t), \ldots, L_{N}(t), t \geqslant 0\right)$ independent at equilibrium? Justify your answer.

  (iii) Let $D_{i}(t)$ be the process of final departures from queue $i$. Show that, at equilibrium, $\left(L_{1}(t), \ldots, L_{N}(t)\right)$ is independent of $\left(D_{i}(s), 1 \leqslant i \leqslant N, 0 \leqslant s \leqslant t\right)$. Show that, for each fixed $i=1, \ldots, N,\left(D_{i}(t), t \geqslant 0\right)$ is a Poisson process, and specify its rate.

  comment

Asymptotic Methods

• Paper 4, Section II, B

  Asymptotic Methods | Part II, 2013

  Show that the equation

  $$\frac{d^{2} y}{d x^{2}}+\frac{2}{x} \frac{d y}{d x}+\left(\frac{1}{x^{2}}-1\right) y=0$$

  has an irregular singular point at infinity. Using the Liouville-Green method, show that one solution has the asymptotic expansion

  $$y(x) \sim \frac{1}{x} e^{x}\left(1+\frac{1}{2 x}+\ldots\right)$$

  as $x \rightarrow \infty$

  comment

Classical Dynamics

• Paper 4, Section I, B

  Classical Dynamics | Part II, 2013

  The Lagrangian for a heavy symmetric top of mass $M$, pinned at point $O$ which is a distance $l$ from the centre of mass, is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  (i) Starting with the fixed space frame $\left(\tilde{\mathbf{e}}_{\mathbf{1}}, \tilde{\mathbf{e}}_{2}, \tilde{\mathbf{e}}_{3}\right)$ and choosing $O$ at its origin, sketch the top with embedded body frame axis $\mathbf{e}_{3}$ being the symmetry axis. Clearly identify the Euler angles $(\theta, \phi, \psi)$.

  (ii) Obtain the momenta $p_{\theta}, p_{\phi}$ and $p_{\psi}$ and the Hamiltonian $H\left(\theta, \phi, \psi, p_{\theta}, p_{\phi}, p_{\psi}\right)$. Derive Hamilton's equations. Identify the three conserved quantities.

  comment

• Paper 4, Section II, B

  Classical Dynamics | Part II, 2013

  The motion of a particle of charge $q$ and mass $m$ in an electromagnetic field with scalar potential $\phi(\mathbf{r}, t)$ and vector potential $\mathbf{A}(\mathbf{r}, t)$ is characterized by the Lagrangian

  $$L=\frac{m \dot{\mathbf{r}}^{2}}{2}-q(\phi-\dot{\mathbf{r}} \cdot \mathbf{A})$$

  (i) Write down the Hamiltonian of the particle.

  (ii) Write down Hamilton's equations of motion for the particle.

  (iii) Show that Hamilton's equations are invariant under the gauge transformation

  $$\phi \rightarrow \phi-\frac{\partial \Lambda}{\partial t}, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda,$$

  for an arbitrary function $\Lambda(\mathbf{r}, t)$.

  (iv) The particle moves in the presence of a field such that $\phi=0$ and $\mathbf{A}=\left(-\frac{1}{2} y B, \frac{1}{2} x B, 0\right)$, where $(x, y, z)$ are Cartesian coordinates and $B$ is a constant.

  (a) Find a gauge transformation such that only one component of $\mathbf{A}(x, y, z)$ remains non-zero.

  (b) Determine the motion of the particle.

  (v) Now assume that $B$ varies very slowly with time on a time-scale much longer than $(q B / m)^{-1}$. Find the quantity which remains approximately constant throughout the motion.

  [You may use the expression for the action variable $I=\frac{1}{2 \pi} \oint p_{i} d q_{i}$.]

  comment

Coding and Cryptography

• Paper 4, Section I, $4 \mathrm{H}$

  Coding and Cryptography | Part II, 2013

  Describe how a stream cipher works. What is a one-time pad?

  A one-time pad is used to send the message $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} y_{7}$ which is encoded as 0101011. In error, it is reused to send the message $y_{0} x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ which is encoded as 0100010 . Show that there are two possibilities for the substring $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$, and find them.

  comment

Cosmology

• Paper 4, Section I, D

  Cosmology | Part II, 2013

  List the relativistic species of bosons and fermions from the standard model of particle physics that are present in the early universe when the temperature falls to $1 \mathrm{MeV} / \mathrm{k}_{B}$.

  Which of the particles above will be interacting when the temperature is above $1 \mathrm{MeV} / k_{B}$ and between $1 \mathrm{MeV} / k_{B} \geq T \geq 0.51 \mathrm{MeV} / k_{B}$, respectively?

  Explain what happens to the populations of particles present when the temperature falls to $0.51 \mathrm{MeV} / k_{B}$.

  The entropy density of fermion and boson species with temperature $T$ is $s \propto g_{s} T^{3}$, where $g_{s}$ is the number of relativistic spin degrees of freedom, that is,

  $$g_{s}=\sum_{\text {bosons }} g_{i}+\frac{7}{8} \sum_{\text {fermions }} g_{i}$$

  Show that when the temperature of the universe falls below $0.51 \mathrm{MeV} / k_{B}$ the ratio of the neutrino and photon temperatures will be given by

  $$\frac{T_{\nu}}{T_{\gamma}}=\left(\frac{4}{11}\right)^{1 / 3}$$

  comment

Differential Geometry

• Paper 4, Section II, H

  Differential Geometry | Part II, 2013

  Define what is meant by the geodesic curvature $k_{g}$ of a regular curve $\alpha: I \rightarrow S$ parametrized by arc length on a smooth oriented surface $S \subset \mathbf{R}^{3}$. If $S$ is the unit sphere in $\mathbf{R}^{3}$ and $\alpha: I \rightarrow S$ is a parametrized geodesic circle of radius $\phi$, with $0<\phi<\pi / 2$, justify the fact that $\left|k_{g}\right|=\cot \phi$.

  State the general form of the Gauss-Bonnet theorem with boundary on an oriented surface $S$, explaining briefly the terms which occur.

  Let $S \subset \mathbf{R}^{3}$ now denote the circular cone given by $z>0$ and $x^{2}+y^{2}=z^{2} \tan ^{2} \phi$, for a fixed choice of $\phi$ with $0<\phi<\pi / 2$, and with a fixed choice of orientation. Let $\alpha: I \rightarrow S$ be a simple closed piecewise regular curve on $S$, with (signed) exterior angles $\theta_{1}, \ldots, \theta_{N}$ at the vertices (that is, $\theta_{i}$ is the angle between limits of tangent directions, with sign determined by the orientation). Suppose furthermore that the smooth segments of $\alpha$ are geodesic curves. What possible values can $\theta_{1}+\cdots+\theta_{N}$ take? Justify your answer.

  [You may assume that a simple closed curve in $\mathbf{R}^{2}$ bounds a region which is homeomorphic to a disc. Given another simple closed curve in the interior of this region, you may assume that the two curves bound a region which is homeomorphic to an annulus.]

  comment

Dynamical Systems

• Paper 4, Section I, C

  Dynamical Systems | Part II, 2013

  Consider the system

  $$\begin{aligned} &\dot{x}=y+a x+b x^{3} \\ &\dot{y}=-x \end{aligned}$$

  What is the Poincaré index of the single fixed point? If there is a closed orbit, why must it enclose the origin?

  By writing $\dot{x}=\partial H / \partial y+g(x)$ and $\dot{y}=-\partial H / \partial x$ for suitable functions $H(x, y)$ and $g(x)$, show that if there is a closed orbit $\mathcal{C}$ then

  $$\oint_{\mathcal{C}}\left(a x+b x^{3}\right) x d t=0$$

  Deduce that there is no closed orbit when $a b>0$.

  If $a b<0$ and $a$ and $b$ are both $O(\epsilon)$, where $\epsilon$ is a small parameter, then there is a single closed orbit that is to within $O(\epsilon)$ a circle of radius $R$ centred on the origin. Deduce a relation between $a, b$ and $R$.

  comment

• Paper 4, Section II, C

  Dynamical Systems | Part II, 2013

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=(x+y+a)(x-y+a) \\ &\dot{y}=y-x^{2}-b \end{aligned}$$

  where $a>0$.

  Find the fixed points of the dynamical system. Show that for any fixed value of $a$ there exist three values $b_{1}>b_{2} \geqslant b_{3}$ of $b$ where a bifurcation occurs. Show that $b_{2}=b_{3}$ when $a=1 / 2$.

  In the remainder of this question set $a=1 / 2$.

  (i) Being careful to explain your reasoning, show that the extended centre manifold for the bifurcation at $b=b_{1}$ can be written in the form $X=\alpha Y+\beta \mu+p(Y, \mu)$, where $X$ and $Y$ denote the departures from the values of $x$ and $y$ at the fixed point, $b=b_{1}+\mu, \alpha$ and $\beta$ are suitable constants (to be determined) and $p$ is quadratic to leading order. Derive a suitable approximate form for $p$, and deduce the nature of the bifurcation and the stability of the different branches of the steady state solution near the bifurcation.

  (ii) Repeat the calculations of part (i) for the bifurcation at $b=b_{2}$.

  (iii) Sketch the $x$ values of the fixed points as functions of $b$, indicating the nature of the bifurcations and where each branch is stable.

  comment

Electrodynamics

• Paper 4, Section II, 35B

  Electrodynamics | Part II, 2013

  (i) For a time-dependent source, confined within a domain $D$, show that the time derivative $\dot{d}$ of the dipole moment $\mathbf{d}$ satisfies

  $$\dot{\mathbf{d}}=\int_{D} d^{3} y \mathbf{J}(\mathbf{y})$$

  where $\mathbf{J}$ is the current density.

  (ii) The vector potential $\mathbf{A}(\mathbf{x}, t)$ due to a time-dependent source is given by

  $$\mathbf{A}=\frac{1}{r} f(t-r / c) \mathbf{k}$$

  where $r=|\mathbf{x}| \neq 0$, and $\mathbf{k}$ is the unit vector in the $z$ direction. Calculate the resulting magnetic field $\mathbf{B}(\mathbf{x}, t)$. By considering the magnetic field for small $r$ show that the dipole moment of the effective source satisfies

  $$\frac{\mu_{0}}{4 \pi} \dot{\mathbf{d}}=f(t) \mathbf{k}$$

  Calculate the asymptotic form of the magnetic field $\mathbf{B}$ at very large $r$.

  (iii) Using the equation

  $$\frac{\partial \mathbf{E}}{\partial t}=c^{2} \nabla \times \mathbf{B}$$

  calculate $\mathbf{E}$ at very large $r$. Show that $\mathbf{E}, \mathbf{B}$ and $\hat{\mathbf{r}}=\mathbf{x} /|\mathbf{x}|$ form a right-handed triad, and moreover $|\mathbf{E}|=c|\mathbf{B}|$. How do $|\mathbf{E}|$ and $|\mathbf{B}|$ depend on $r ?$ What is the significance of this?

  (iv) Calculate the power $P(\theta, \phi)$ emitted per unit solid angle and sketch its dependence on $\theta$. Show that the emitted radiation is polarised and describe how the plane of polarisation (that is, the plane in which $\mathbf{E}$ and $\hat{\mathbf{r}}$ lie) depends on the direction of the dipole. Suppose the dipole moment has constant amplitude and constant frequency and so the radiation is monochromatic with wavelength $\lambda$. How does the emitted power depend on $\lambda$ ?

  comment

Fluid Dynamics II

• Paper 4, Section II, A

  Fluid Dynamics II | Part II, 2013

  Consider the flow of an incompressible fluid of uniform density $\rho$ and dynamic viscosity $\mu$. Show that the rate of viscous dissipation per unit volume is given by

  $$\Phi=2 \mu e_{i j} e_{i j}$$

  where $e_{i j}$ is the strain rate.

  Determine expressions for $e_{i j}$ and $\Phi$ when the flow is irrotational with velocity potential $\phi$.

  In deep water a linearised wave with a surface displacement $\eta=a \cos (k x-\omega t)$ has a velocity potential $\phi=-(\omega a / k) e^{-k z} \sin (k x-\omega t)$. Hence determine the rate of the viscous dissipation, averaged over a wave period $2 \pi / \omega$, for an irrotational surface wave of wavenumber $k$ and small amplitude $a \ll 1 / k$ in a fluid with very small viscosity $\mu \ll \rho \omega / k^{2}$ and great depth $H \gg 1 / k$.

  Calculate the depth-integrated kinetic energy per unit wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order as $e^{-\gamma t}$, where $\gamma$ should be found.

  comment

Further Complex Methods

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2013

  Let the function $f(z)$ be analytic in the upper half-plane and such that $|f(z)| \rightarrow 0$ as $|z| \rightarrow \infty$. Show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x} d x=i \pi f(0),$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  Use the Cauchy integral theorem to show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{u(x, 0)}{x-t} d x=-\pi v(t, 0), \quad \mathcal{P} \int_{-\infty}^{\infty} \frac{v(x, 0)}{x-t} d x=\pi u(t, 0),$$

  where $u(x, y)$ and $v(x, y)$ are the real and imaginary parts of $f(z)$.

  comment

Galois Theory

• Paper 4, Section II, I

  Galois Theory | Part II, 2013

  (i) Let $\zeta_{N}=\mathrm{e}^{2 \pi i / N} \in \mathbb{C}$ for $N \geqslant 1$. For the cases $N=11,13$, is it possible to express $\zeta_{N}$, starting with integers and using rational functions and (possibly nested) radicals? If it is possible, briefly explain how this is done, assuming standard facts in Galois Theory.

  (ii) Let $F=\mathbb{C}(X, Y, Z)$ be the rational function field in three variables over $\mathbb{C}$, and for integers $a, b, c \geqslant 1$ let $K=\mathbb{C}\left(X^{a}, Y^{b}, Z^{c}\right)$ be the subfield of $F$ consisting of all rational functions in $X^{a}, Y^{b}, Z^{c}$ with coefficients in $\mathbb{C}$. Show that $F / K$ is Galois, and determine its Galois group. [Hint: For $\alpha, \beta, \gamma \in \mathbb{C}^{\times}$, the map $(X, Y, Z) \longmapsto(\alpha X, \beta Y, \gamma Z)$ is an automorphism of $F$.]

  comment

General Relativity

• Paper 4, Section II, D

  General Relativity | Part II, 2013

  Consider the metric describing the interior of a star,

  $$d s^{2}=-e^{2 \alpha(r)} d t^{2}+e^{2 \beta(r)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  defined for $0 \leqslant r \leqslant r_{0}$ by

  $$e^{\alpha(r)}=\frac{3}{2} e^{-\beta_{0}}-\frac{1}{2} e^{-\beta(r)},$$

  with

  $$e^{-2 \beta(r)}=1-A r^{2}$$

  Here $A=2 M / r_{0}^{3}$, where $M$ is the mass of the star, $\beta_{0}=\beta\left(r_{0}\right)$, and we have taken units in which we have set $G=c=1$.

  (i) The star is made of a perfect fluid with energy-momentum tensor

  $$T_{a b}=(p+\rho) u_{a} u_{b}+p g_{a b}$$

  Here $u^{a}$ is the 4-velocity of the fluid which is at rest, the density $\rho$ is constant throughout the star $\left(0 \leqslant r \leqslant r_{0}\right)$ and the pressure $p=p(r)$ depends only on the radial coordinate. Write down the Einstein field equations and show that they may be written as

  $$R_{a b}=8 \pi(p+\rho) u_{a} u_{b}+4 \pi(\rho-p) g_{a b}$$

  (ii) Using the formulae given below, or otherwise, show that for $0 \leqslant r \leqslant r_{0}$, one has

  $$\begin{aligned} &4 \pi(\rho+p)=\frac{\left(\alpha^{\prime}+\beta^{\prime}\right)}{r} e^{-2 \beta(r)} \\ &4 \pi(\rho-p)=\left(\frac{\beta^{\prime}-\alpha^{\prime}}{r}-\frac{1}{r^{2}}\right) e^{-2 \beta(r)}+\frac{1}{r^{2}} \end{aligned}$$

  where primes denote differentiation with respect to $r$. Hence show that

  $$\rho=\frac{3 A}{8 \pi} \quad, \quad p(r)=\frac{3 A}{8 \pi}\left(\frac{e^{-\beta(r)}-e^{-\beta_{0}}}{3 e^{-\beta_{0}}-e^{-\beta(r)}}\right)$$

  [The non-zero components of the Ricci tensor are

  $$\begin{aligned} &R_{00}=e^{2 \alpha-2 \beta}\left(\alpha^{\prime \prime}-\alpha^{\prime} \beta^{\prime}+\alpha^{\prime 2}+\frac{2 \alpha^{\prime}}{r}\right) \\ &R_{11}=-\alpha^{\prime \prime}+\alpha^{\prime} \beta^{\prime}-\alpha^{\prime 2}+\frac{2 \beta^{\prime}}{r} \\ &R_{22}=1+e^{-2 \beta}\left[\left(\beta^{\prime}-\alpha^{\prime}\right) r-1\right] \\ &R_{33}=\sin ^{2} \theta R_{22} \end{aligned}$$

  Note that

  $$\left.\alpha^{\prime}=\frac{1}{2} A r e^{\beta-\alpha} \quad, \quad \beta^{\prime}=A r e^{2 \beta} .\right]$$

  comment

Geometry and Groups

• Paper 4, Section I, $3 G$

  Geometry and Groups | Part II, 2013

  Let $\Delta_{1}, \Delta_{2}$ be two disjoint closed discs in the Riemann sphere with bounding circles $\Gamma_{1}, \Gamma_{2}$ respectively. Let $J_{k}$ be inversion in the circle $\Gamma_{k}$ and let $T$ be the Möbius transformation $J_{2} \circ J_{1}$.

  Show that, if $w \notin \Delta_{1}$, then $T(w) \in \Delta_{2}$ and so $T^{n}(w) \in \Delta_{2}$ for $n=1,2,3, \ldots$ Deduce that $T$ has a fixed point in $\Delta_{2}$ and a second in $\Delta_{1}$.

  Deduce that there is a Möbius transformation $A$ with

  $$A\left(\Delta_{1}\right)=\{z:|z| \leqslant 1\} \quad \text { and } \quad A\left(\Delta_{2}\right)=\{z:|z| \geqslant R\}$$

  for some $R>1$.

  comment

• Paper 4, Section II, $12 \mathrm{G}$

  Geometry and Groups | Part II, 2013

  Define the limit set for a Kleinian group. If your definition of the limit set requires an arbitrary choice of a base point, you should prove that the limit set does not depend on this choice.

  Let $\Delta_{1}, \Delta_{2}, \Delta_{3}, \Delta_{4}$ be the four discs $\{z \in \mathbb{C}:|z-c| \leqslant 1\}$ where $c$ is the point $1+i, 1-i,-1-i,-1+i$ respectively. Show that there is a parabolic Möbius transformation $A$ that maps the interior of $\Delta_{1}$ onto the exterior of $\Delta_{2}$ and fixes the point where $\Delta_{1}$ and $\Delta_{2}$ touch. Show further that we can choose $A$ so that it maps the unit disc onto itself.

  Let $B$ be the similar parabolic transformation that maps the interior of $\Delta_{3}$ onto the exterior of $\Delta_{4}$, fixes the point where $\Delta_{3}$ and $\Delta_{4}$ touch, and maps the unit disc onto itself. Explain why the group generated by $A$ and $B$ is a Kleinian group $G$. Find the limit set for the group $G$ and justify your answer.

  comment

Graph Theory

• Paper 4, Section II, F

  Graph Theory | Part II, 2013

  Define the maximum degree $\Delta(G)$ and the chromatic index $\chi^{\prime}(G)$ of the graph $G$.

  State and prove Vizing's theorem relating $\Delta(G)$ and $\chi^{\prime}(G)$.

  Let $G$ be a connected graph such that $\chi^{\prime}(G)=\Delta(G)+1$ but, for every subgraph $H$ of $G, \chi^{\prime}(H)=\Delta(H)$ holds. Show that $G$ is a circuit of odd length.

  comment

Linear Analysis

• Paper 4, Section II, F

  Linear Analysis | Part II, 2013

  Let $T: X \rightarrow X$ be a bounded linear operator on a complex Banach space $X$. Define the spectrum $\sigma(T)$ of $T$. What is an approximate eigenvalue of $T$ ? What does it mean to say that $T$ is compact?

  Assume now that $T$ is compact. Show that if $\lambda$ is in the boundary of $\sigma(T)$ and $\lambda \neq 0$, then $\lambda$ is an eigenvalue of $T$. [You may use without proof the result that every $\lambda$ in the boundary of $\sigma(T)$ is an approximate eigenvalue of $T$.]

  Let $T: H \rightarrow H$ be a compact Hermitian operator on a complex Hilbert space $H$. Prove the following:

  (a) If $\lambda \in \sigma(T)$ and $\lambda \neq 0$, then $\lambda$ is an eigenvalue of $T$.

  (b) $\sigma(T)$ is countable.

  comment

Logic and Set Theory

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2013

  State the Axiom of Foundation and the Principle of $\in$-Induction, and show that they are equivalent in the presence of the other axioms of ZF set theory. [You may assume the existence of transitive closures.]

  Given a model $(V, \in)$ for all the axioms of ZF except Foundation, show how to define a transitive class $R$ which, with the restriction of the given relation $\in$, is a model of ZF.

  Given a model $(V, \in)$ of $\mathrm{ZF}$, indicate briefly how one may modify the relation $\in$ so that the resulting structure $\left(V, \in^{\prime}\right)$ fails to satisfy Foundation, but satisfies all the other axioms of $\mathrm{ZF}$. [You need not verify that all the other axioms hold in $\left(V, \in^{\prime}\right)$.]

  comment

Mathematical Biology

• Paper 4, Section I, A

  Mathematical Biology | Part II, 2013

  A model of two populations competing for resources takes the form

  $$\begin{aligned} \frac{d n_{1}}{d t} &=r_{1} n_{1}\left(1-n_{1}-a_{12} n_{2}\right) \\ \frac{d n_{2}}{d t} &=r_{2} n_{2}\left(1-n_{2}-a_{21} n_{1}\right) \end{aligned}$$

  where all parameters are positive. Give a brief biological interpretation of $a_{12}, a_{21}, r_{1}$ and $r_{2}$. Briefly describe the dynamics of each population in the absence of the other.

  Give conditions for there to exist a steady-state solution with both populations present (that is, $n_{1}>0$ and $n_{2}>0$ ), and give conditions for this solution to be stable.

  In the case where there exists a solution with both populations present but the solution is not stable, what is the likely long-term outcome for the biological system? Explain your answer with the aid of a phase diagram in the $\left(n_{1}, n_{2}\right)$ plane.

  comment

Number Fields

• Paper 4, Section II, H

  Number Fields | Part II, 2013

  State Dedekind's criterion. Use it to factor the primes up to 5 in the ring of integers $\mathcal{O}_{K}$ of $K=\mathbb{Q}(\sqrt{65})$. Show that every ideal in $\mathcal{O}_{K}$ of norm 10 is principal, and compute the class group of $K$.

  comment

Number Theory

• Paper 4, Section I, I

  Number Theory | Part II, 2013

  Let $s=\sigma+i t$ with $\sigma, t \in \mathbb{R}$. Define the Riemann zeta function $\zeta(s)$ for $\sigma>1$. Show that for $\sigma>1$,

  $$\zeta(s)=\prod_{p}\left(1-p^{-s}\right)^{-1}$$

  where the product is taken over all primes. Deduce that there are infinitely many primes.

  comment

• Paper 4, Section II, I

  Number Theory | Part II, 2013

  (i) What is meant by the continued fraction expansion of a real number $\theta$ ? Suppose that $\theta$ has continued fraction $\left[a_{0}, a_{1}, a_{2}, \ldots\right]$. Define the convergents $p_{n} / q_{n}$ to $\theta$ and give the recurrence relations satisfied by the $p_{n}$ and $q_{n}$. Show that the convergents $p_{n} / q_{n}$ do indeed converge to $\theta$.

  [You need not justify the basic order properties of finite continued fractions.]

  (ii) Find two solutions in strictly positive integers to each of the equations

  $$x^{2}-10 y^{2}=1 \quad \text { and } \quad x^{2}-11 y^{2}=1$$

  comment

Numerical Analysis

• Paper 4, Section II, C

  Numerical Analysis | Part II, 2013

  Consider the solution of the two-point boundary value problem

  $$(2-\sin \pi x) u^{\prime \prime}+u=1, \quad-1 \leqslant x \leqslant 1$$

  with periodic boundary conditions at $x=-1$ and $x=1$. Construct explicitly the linear algebraic system that arises from the application of a spectral method to the above equation.

  The Fourier coefficients of $u$ are defined by

  $$\hat{u}_{n}=\frac{1}{2} \int_{-1}^{1} u(\tau) e^{-i \pi n \tau} d \tau$$

  Prove that the computation of the Fourier coefficients for the truncated system with $-N / 2+1 \leqslant n \leqslant N / 2$ (where $N$ is an even and positive integer, and assuming that $\hat{u}_{n}=0$ outside this range of $n$ ) reduces to the solution of a tridiagonal system of algebraic equations, which you should specify.

  Explain the term convergence with spectral speed and justify its validity for the derived approximation of $u$.

  comment

Optimization and Control

• Paper 4, Section II, K

  Optimization and Control | Part II, 2013

  Given $r, \rho, \mu, T$, all positive, it is desired to choose $u(t)>0$ to maximize

  $$\mu x(T)+\int_{0}^{T} e^{-\rho t} \log u(t) d t$$

  subject to $\dot{x}(t)=r x(t)-u(t), x(0)=10$.

  Explain what Pontryagin's maximum principle guarantees about a solution to this problem.

  Show that no matter whether $x(T)$ is constrained or unconstrained there is a constant $\alpha$ such that the optimal control is of the form $u(t)=\alpha e^{-(\rho-r) t}$. Find an expression for $\alpha$ under the constraint $x(T)=5$.

  Show that if $x(T)$ is unconstrained then $\alpha=(1 / \mu) e^{-r T}$.

  comment

Partial Differential Equations

• Paper 4, Section II, C

  Partial Differential Equations | Part II, 2013

  (i) Show that an arbitrary $C^{2}$ solution of the one-dimensional wave equation $u_{t t}-u_{x x}=0$ can be written in the form $u=F(x-t)+G(x+t)$.

  Hence, deduce the formula for the solution at arbitrary $t>0$ of the Cauchy problem

  $$u_{t t}-u_{x x}=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x)$$

  where $u_{0}, u_{1}$ are arbitrary Schwartz functions.

  Deduce from this formula a theorem on finite propagation speed for the onedimensional wave equation.

  (ii) Define the Fourier transform of a tempered distribution. Compute the Fourier transform of the tempered distribution $T_{t} \in \mathcal{S}^{\prime}(\mathbb{R})$ defined for all $t>0$ by the function

  $$T_{t}(y)= \begin{cases}\frac{1}{2} & \text { if }|y| \leqslant t \\ 0 & \text { if }|y|>t\end{cases}$$

  that is, $\left\langle T_{t}, f\right\rangle=\frac{1}{2} \int_{-t}^{+t} f(y) d y$ for all $f \in \mathcal{S}(\mathbb{R})$. By considering the Fourier transform in $x$, deduce from this the formula for the solution of $(*)$ that you obtained in part (i) in the case $u_{0}=0$.

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, E

  Principles of Quantum Mechanics | Part II, 2013

  (i) The creation and annihilation operators for a harmonic oscillator of angular frequency $\omega$ satisfy the commutation relation $\left[a, a^{\dagger}\right]=1$. Write down an expression for the Hamiltonian $H$ and number operator $N$ in terms of $a$ and $a^{\dagger}$. Explain how the space of eigenstates $|n\rangle, n=0,1,2, \ldots$, of $H$ is formed, and deduce the eigenenergies for these states. Show that

  $$a|n\rangle=\sqrt{n}|n-1\rangle, \quad a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle$$

  (ii) The operator $K_{r}$ is defined to be

  $$K_{r}=\frac{\left(a^{\dagger}\right)^{r} a^{r}}{r !}$$

  for $r=0,1,2, \ldots$ Show that $K_{r}$ commutes with $N$. Show that if $r \leqslant n$, then

  $$K_{r}|n\rangle=\frac{n !}{(n-r) ! r !}|n\rangle,$$

  and $K_{r}|n\rangle=0$ otherwise. By considering the action of $K_{r}$ on the state $|n\rangle$, deduce that

  $$\sum_{r=0}^{\infty}(-1)^{r} K_{r}=|0\rangle\langle 0|$$

  comment

Principles of Statistics

• Paper 4, Section II, $27 \mathrm{~K}$

  Principles of Statistics | Part II, 2013

  Assuming only the existence and properties of the univariate normal distribution, define $\mathcal{N}_{p}(\underline{\mu}, \Sigma)$, the multivariate normal distribution with mean (row-)vector $\underline{\mu}$ and dispersion matrix $\Sigma$; and $W_{p}(\nu ; \Sigma)$, the Wishart distribution on integer $\nu>1$ degrees of freedom and with scale parameter $\Sigma$. Show that, if $\underline{X} \sim \mathcal{N}_{p}(\underline{\mu}, \Sigma), S \sim W_{p}(\nu ; \Sigma)$, and $\underline{b}(1 \times q), A(p \times q)$ are fixed, then $\underline{b}+\underline{X} A \sim \mathcal{N}_{q}(\underline{b}+\underline{\mu} A, \Phi), A^{\mathrm{T}} S A \sim W_{p}(\nu ; \Phi)$, where $\Phi=A^{\mathrm{T}} \Sigma A$.

  The random $(n \times p)$ matrix $X$ has rows that are independently distributed as $\mathcal{N}_{p}(\underline{\mathrm{M}}, \Sigma)$, where both parameters $\underline{\mathrm{M}}$ and $\Sigma$ are unknown. Let $\underline{\bar{X}}:=n^{-1} \mathbf{1}^{\mathrm{T}} X$, where 1 is the $(n \times 1)$ vector of $1 \mathrm{~s}$; and $S^{c}:=X^{\mathrm{T}} \Pi X$, with $\Pi:=I_{n}-n^{-1} 11^{\mathrm{T}}$. State the joint distribution of $\bar{X}$ and $S^{c}$ given the parameters.

  Now suppose $n>p$ and $\Sigma$ is positive definite. Hotelling's $T^{2}$ is defined as

  $$T^{2}:=n(\underline{\bar{X}}-\underline{\mathrm{M}})\left(\bar{S}^{c}\right)^{-1}(\underline{\bar{X}}-\underline{\mathrm{M}})^{\mathrm{T}}$$

  where $\bar{S}^{c}:=S^{c} / \nu$ with $\nu:=(n-1)$. Show that, for any values of $\underline{\mathrm{M}}$ and $\Sigma$,

  $$\left(\frac{\nu-p+1}{\nu p}\right) T^{2} \sim F_{\nu-p+1}^{p},$$

  the $F$ distribution on $p$ and $\nu-p+1$ degrees of freedom.

  [You may assume that:

  1. If $S \sim W_{p}(\nu ; \Sigma)$ and $\mathbf{a}$ is a fixed $(p \times 1)$ vector, then

  $$\frac{\mathbf{a}^{\mathrm{T}} \Sigma^{-1} \mathbf{a}}{\mathbf{a}^{\mathrm{T}} S^{-1} \mathbf{a}} \sim \chi_{\nu-p+1}^{2}$$

  2. If $V \sim \chi_{p}^{2}, W \sim \chi_{\lambda}^{2}$ are independent, then

  $$\frac{V / p}{W / \lambda} \sim F_{\lambda}^{p} \text {. }$$

  comment

Probability and Measure

• Paper 4, Section II, K

  Probability and Measure | Part II, 2013

  State Birkhoff's almost-everywhere ergodic theorem.

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables such that

  $$\mathbb{P}\left(X_{n}=0\right)=\mathbb{P}\left(X_{n}=1\right)=1 / 2$$

  Define for $k \in \mathbb{N}$

  $$Y_{k}=\sum_{n=1}^{\infty} X_{k+n-1} / 2^{n}$$

  What is the distribution of $Y_{k} ? \quad$ Show that the random variables $Y_{1}$ and $Y_{2}$ are not independent.

  Set $S_{n}=Y_{1}+\cdots+Y_{n}$. Show that $S_{n} / n$ converges as $n \rightarrow \infty$ almost surely and determine the limit. [You may use without proof any standard theorem provided you state it clearly.]

  comment

Representation Theory

• Paper 4, Section II, G

  Representation Theory | Part II, 2013

  State and prove Burnside's $p^{a} q^{b}$-theorem.

  comment

Statistical Modelling

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2013

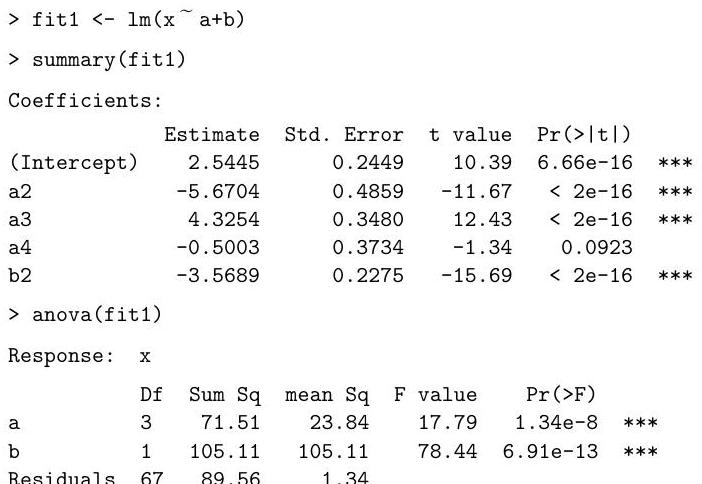
  The output $X$ of a process depends on the levels of two adjustable variables: $A$, a factor with four levels, and $B$, a factor with two levels. For each combination of a level of $A$ and a level of $B$, nine independent values of $X$ are observed.

  Explain and interpret the $R$ commands and (abbreviated) output below. In particular, describe the model being fitted, and describe and comment on the hypothesis tests performed under the summary and anova commands.

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2013

  Let $f_{0}$ be a probability density function, with cumulant generating function $K$. Define what it means for a random variable $Y$ to have a model function of exponential dispersion family form, generated by $f_{0}$.

  A random variable $Y$ is said to have an inverse Gaussian distribution, with parameters $\phi$ and $\lambda$ (both positive), if its density function is

  $$f(y ; \phi, \lambda)=\frac{\sqrt{\lambda}}{\sqrt{2 \pi y^{3}}} e^{\sqrt{\lambda \phi}} \exp \left\{-\frac{1}{2}\left(\frac{\lambda}{y}+\phi y\right)\right\} \quad(y>0)$$

  Show that the family of all inverse Gaussian distributions for $Y$ is of exponential dispersion family form. Deduce directly the corresponding expressions for $E(Y)$ and $\operatorname{Var}(Y)$ in terms of $\phi$ and $\lambda$. What are the corresponding canonical link function and variance function?

  Consider a generalized linear model, $M$, for independent variables $Y_{i}(i=1, \ldots, n)$, whose random component is defined by the inverse Gaussian distribution with link function $g(\mu)=\log (\mu):$ thus $g\left(\mu_{i}\right)=x_{i}^{\mathrm{T}} \beta$, where $\beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{\mathrm{T}}$ is the vector of unknown regression coefficients and $x_{i}=\left(x_{i 1}, \ldots, x_{i p}\right)^{\mathrm{T}}$ is the vector of known values of the explanatory variables for the $i^{\text {th }}$observation. The vectors $x_{i}(i=1, \ldots, n)$ are linearly independent. Assuming that the dispersion parameter is known, obtain expressions for the score function and Fisher information matrix for $\beta$. Explain how these can be used to compute the maximum likelihood estimate $\widehat{\beta}$ of $\beta$.

  comment

Statistical Physics

• Paper 4, Section II, A

  Statistical Physics | Part II, 2013

  A classical particle of mass $m$ moving non-relativistically in two-dimensional space is enclosed inside a circle of radius $R$ and attached by a spring with constant $\kappa$ to the centre of the circle. The particle thus moves in a potential

  $$V(r)= \begin{cases}\frac{1}{2} \kappa r^{2} & \text { for } r<R \\ \infty & \text { for } r \geqslant R\end{cases}$$

  where $r^{2}=x^{2}+y^{2}$. Let the particle be coupled to a heat reservoir at temperature $T$.

  (i) Which of the ensembles of statistical physics should be used to model the system?

  (ii) Calculate the partition function for the particle.

  (iii) Calculate the average energy $\langle E\rangle$ and the average potential energy $\langle V\rangle$ of the particle.

  (iv) What is the average energy in:

  (a) the limit $\frac{1}{2} \kappa R^{2} \gg k_{\mathrm{B}} T$ (strong coupling)?

  (b) the limit $\frac{1}{2} \kappa R^{2} \ll k_{\mathrm{B}} T$ (weak coupling)?

  Compare the two results with the values expected from equipartition of energy.

  comment

Stochastic Financial Models

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2013

  Let $S_{t}:=\left(S_{t}^{1}, S_{t}^{2}, \ldots, S_{t}^{n}\right)^{\mathrm{T}}$ denote the time- $t$ prices of $n$ risky assets in which an agent may invest, $t=0,1$. He may also invest his money in a bank account, which will return interest at rate $r>0$. At time 0 , he knows $S_{0}$ and $r$, and he knows that $S_{1} \sim N(\mu, V)$. If he chooses at time 0 to invest cash value $\theta_{i}$ in risky asset $i$, express his wealth $w_{1}$ at time 1 in terms of his initial wealth $w_{0}>0$, the choices $\theta:=\left(\theta_{1}, \ldots, \theta_{n}\right)^{\mathrm{T}}$, the value of $S_{1}$, and $r$.

  Suppose that his goal is to minimize the variance of $w_{1}$ subject to the requirement that the mean $E\left(w_{1}\right)$ should be at least $m$, where $m \geqslant(1+r) w_{0}$ is given. What portfolio $\theta$ should he choose to achieve this?

  Suppose instead that his goal is to minimize $E\left(w_{1}^{2}\right)$ subject to the same constraint. Show that his optimal portfolio is unchanged.

  comment

Topics in Analysis

• Paper 4, Section I, F

  Topics in Analysis | Part II, 2013

  State the Baire Category Theorem. A set $X \subseteq \mathbb{R}$ is said to be a $G_{\delta}$-set if it is the intersection of countably many open sets. Show that the set $\mathbb{Q}$ of rationals is not a $G_{\delta}$-set.

  [You may assume that the rationals are countable and that $\mathbb{R}$ is complete.]

  comment

Waves

• Paper 4, Section II, 38C

  Waves | Part II, 2013

  A wave disturbance satisfies the equation

  $$\frac{\partial^{2} \psi}{\partial t^{2}}-c^{2} \frac{\partial^{2} \psi}{\partial x^{2}}+c^{2} \psi=0$$

  where $c$ is a positive constant. Find the dispersion relation, and write down the solution to the initial-value problem for which $\partial \psi / \partial t(x, 0)=0$ for all $x$, and $\psi(x, 0)$ is given in the form

  $$\psi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  where $A(k)$ is a real function with $A(k)=A(-k)$, so that $\psi(x, 0)$ is real and even.

  Use the method of stationary phase to obtain an approximation to $\psi(x, t)$ for large $t$, with $x / t$ taking the constant value $V$, and $0 \leqslant V<c$. Explain briefly why your answer is inappropriate if $V>c$.

  [You are given that

  $$\left.\int_{-\infty}^{\infty} \exp \left(i u^{2}\right) d u=\pi^{1 / 2} e^{i \pi / 4} .\right]$$

  comment