Part II, 2013, Paper 3

Algebraic Geometry

• Paper 3, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $C \subset \mathbb{P}^{2}$ be the plane curve given by the polynomial

  $$X_{0}^{n}-X_{1}^{n}-X_{2}^{n}$$

  over the field of complex numbers, where $n \geqslant 3$.

  (i) Show that $C$ is nonsingular.

  (ii) Compute the divisors of the rational functions

  $$x=\frac{X_{1}}{X_{0}}, \quad y=\frac{X_{2}}{X_{0}}$$

  on $C$.

  (iii) Consider the morphism $\phi=\left(X_{0}: X_{1}\right): C \rightarrow \mathbb{P}^{1}$. Compute its ramification points and degree.

  (iv) Show that a basis for the space of regular differentials on $C$ is

  $$\left\{x^{i} y^{j} \omega_{0} \mid i, j \geqslant 0, i+j \leqslant n-3\right\}$$

  where $\omega_{0}=d x / y^{n-1} .$

  comment

Algebraic Topology

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Mayer-Vietoris theorem for the homology groups of polyhedra.

  (ii) Calculate the homology groups of the $n$-sphere, for every $n \geqslant 0$.

  (iii) Suppose that $a \geqslant 1$ and $b \geqslant 0$. Calculate the homology groups of the subspace $X$ of $\mathbb{R}^{a+b}$ defined by $\sum_{i=1}^{a} x_{i}^{2}-\sum_{j=a+1}^{a+b} x_{j}^{2}=1$.

  comment

Applications of Quantum Mechanics

• Paper 3, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  Write down the classical Hamiltonian for a particle of mass $m$, electric charge $-e$ and momentum p moving in the background of an electromagnetic field with vector and scalar potentials $\mathbf{A}(\mathbf{x}, t)$ and $\phi(\mathbf{x}, t)$.

  Consider the case of a constant uniform magnetic field, $\mathbf{B}=(0,0, B)$ and $\mathbf{E}=0$. Working in the gauge with $\mathbf{A}=(-B y, 0,0)$ and $\phi=0$, show that Hamilton's equations,

  $$\dot{\mathbf{x}}=\frac{\partial H}{\partial \mathbf{p}}, \quad \dot{\mathbf{p}}=-\frac{\partial H}{\partial \mathbf{x}},$$

  admit solutions corresponding to circular motion in the $x-y$ plane with angular frequency $\omega_{B}=e B / m$.

  Show that, in the same gauge, the coordinates $\left(x_{0}, y_{0}, 0\right)$ of the centre of the circle are related to the instantaneous position $\mathbf{x}=(x, y, z)$ and momentum $\mathbf{p}=\left(p_{x}, p_{y}, p_{z}\right)$ of the particle by

  $$x_{0}=x-\frac{p_{y}}{e B}, \quad y_{0}=\frac{p_{x}}{e B} .$$

  Write down the quantum Hamiltonian $\hat{H}$ for the system. In the case of a uniform constant magnetic field discussed above, find the allowed energy levels. Working in the gauge specified above, write down quantum operators corresponding to the classical quantities $x_{0}$ and $y_{0}$ defined in (1) above and show that they are conserved.

  [In this question you may use without derivation any facts relating to the energy spectrum of the quantum harmonic oscillator provided they are stated clearly.]

  comment

Applied Probability

• Paper 3, Section II, J

  Applied Probability | Part II, 2013

  Define the Moran model. Describe briefly the infinite sites model of mutations.

  We henceforth consider a population with $N$ individuals evolving according to the rules of the Moran model. In addition we assume:

  • the allelic type of any individual at any time lies in a given countable state space $S$;

  • individuals are subject to mutations at constant rate $u=\theta / N$, independently of the population dynamics;

  • each time a mutation occurs, if the allelic type of the individual was $x \in S$, it changes to $y \in S$ with probability $P(x, y)$, where $P(x, y)$ is a given Markovian transition matrix on $S$ that is symmetric:

  $$P(x, y)=P(y, x) \quad(x, y \in S)$$

  (i) Show that, if two individuals are sampled at random from the population at some time $t$, then the time to their most recent common ancestor has an exponential distribution, with a parameter that you should specify.

  (ii) Let $\Delta+1$ be the total number of mutations that accumulate on the two branches separating these individuals from their most recent common ancestor. Show that $\Delta+1$ is a geometric random variable, and specify its probability parameter $p$.

  (iii) The first individual is observed to be of type $x \in S$. Explain why the probability that the second individual is also of type $x$ is

  $$\mathbb{P}\left(X_{\Delta}=x \mid X_{0}=x\right),$$

  where $\left(X_{n}, n \geqslant 0\right)$ is a Markov chain on $S$ with transition matrix $P$ and is independent of $\Delta$.

  comment

Asymptotic Methods

• Paper 3, Section II, B

  Asymptotic Methods | Part II, 2013

  Let

  $$I(x)=\int_{0}^{\pi} f(t) e^{i x \psi(t)} d t$$

  where $f(t)$ and $\psi(t)$ are smooth, and $\psi^{\prime}(t) \neq 0$ for $t>0 ;$ also $f(0) \neq 0$, $\psi(0)=a$, $\psi^{\prime}(0)=\psi^{\prime \prime}(0)=0$ and $\psi^{\prime \prime \prime}(0)=6 b>0$. Show that, as $x \rightarrow+\infty$,

  $$I(x) \sim f(0) e^{i(x a+\pi / 6)}\left(\frac{1}{27 b x}\right)^{1 / 3} \Gamma(1 / 3) .$$

  Consider the Bessel function

  $$J_{n}(x)=\frac{1}{\pi} \int_{0}^{\pi} \cos (n t-x \sin t) d t$$

  Show that, as $n \rightarrow+\infty$,

  $$J_{n}(n) \sim \frac{\Gamma(1 / 3)}{\pi} \frac{1}{(48)^{1 / 6}} \frac{1}{n^{1 / 3}}$$

  comment

Classical Dynamics

• Paper 3, Section I, B

  Classical Dynamics | Part II, 2013

  Two equal masses $m$ are connected to each other and to fixed points by three springs of force constant $5 k, k$ and $5 k$ as shown in the figure.

  

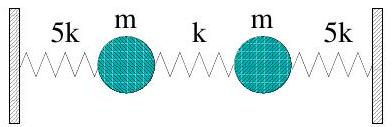
  (i) Write down the Lagrangian and derive the equations describing the motion of the system in the direction parallel to the springs.

  (ii) Find the normal modes and their frequencies. Comment on your results.

  comment

Coding and Cryptography

• Paper 3, Section I, H

  Coding and Cryptography | Part II, 2013

  Describe briefly the Rabin cipher with modulus $N$, explaining how it can be deciphered by the intended recipient and why it is difficult for an eavesdropper to decipher it.

  The Cabinet decides to communicate using Rabin ciphers to maintain confidentiality. The Cabinet Secretary encrypts a message, represented as a positive integer $m$, using the Rabin cipher with modulus $N$ (with $0<m<N$ ) and publishes both the encrypted message and the modulus. The Defence Secretary deciphers this message to read it but then foolishly encrypts it again using a Rabin cipher with a different modulus $N^{\prime}$ (with $\left.m<N^{\prime}\right)$ and publishes the newly encrypted message and $N^{\prime}$. Mr Rime (the Leader of the Opposition) knows this has happened. Explain how Rime can work out what the original message was using the two different encrypted versions.

  Can Rime decipher other messages sent out by the Cabinet using the original modulus $N$ ?

  comment

Cosmology

• Paper 3, Section I, D

  Cosmology | Part II, 2013

  The number densities of protons of mass $m_{p}$ or neutrons of mass $m_{n}$ in kinetic equilibrium at temperature $T$, in the absence of any chemical potentials, are each given by (with $i=n$ or $p$ )

  $$n_{i}=g_{i}\left(\frac{m_{i} k_{B} T}{2 \pi \hbar^{2}}\right)^{3 / 2} \exp \left[-m_{i} c^{2} / k_{B} T\right]$$

  where $k_{B}$ is Boltzmann's constant and $g_{i}$ is the spin degeneracy.

  Use this to show, to a very good approximation, that the ratio of the number of neutrons to protons at a temperature $T \simeq 1 \mathrm{MeV} / k_{B}$ is given by

  $$\frac{n_{n}}{n_{p}}=\exp \left[-\left(m_{n}-m_{p}\right) c^{2} / k_{B} T\right]$$

  where $\left(m_{n}-m_{p}\right) c^{2}=1.3 \mathrm{MeV}$. Explain any approximations you have used.

  The reaction rate for weak interactions between protons and neutrons at energies $5 \mathrm{MeV} \geqslant k_{B} T \geqslant 0.8 \mathrm{MeV}$ is given by $\Gamma=\left(k_{B} T / 1 \mathrm{MeV}\right)^{5} \mathrm{~s}^{-1}$ and the expansion rate of the universe at these energies is given by $H=\left(k_{B} T / 1 M e V\right)^{2} s^{-1}$. Give an example of a weak interaction that can maintain equilibrium abundances of protons and neutrons at these energies. Show how the final abundance of neutrons relative to protons can be calculated and use it to estimate the mass fraction of the universe in helium- 4 after nucleosynthesis.

  What would have happened to the helium abundance if the proton and neutron masses had been exactly equal?

  comment

• Paper 3, Section II, D

  Cosmology | Part II, 2013

  The contents of a spatially homogeneous and isotropic universe are modelled as a finite mass $M$ of pressureless material whose radius $r(t)$ evolves from some constant reference radius $r_{0}$ in proportion to the time-dependent scale factor $a(t)$, with

  $$r(t)=a(t) r_{0}$$

  (i) Show that this motion leads to expansion governed by Hubble's Law. If this universe is expanding, explain why there will be a shift in the frequency of radiation between its emission from a distant object and subsequent reception by an observer. Define the redshift $z$ of the observed object in terms of the values of the scale factor $a(t)$ at the times of emission and reception.

  (ii) The expanding universal mass $M$ is given a small rotational perturbation, with angular velocity $\omega$, and its angular momentum is subsequently conserved. If deviations from spherical expansion can be neglected, show that its linear rotational velocity will fall as $V \propto a^{-n}$, where you should determine the value of $n$. Show that this perturbation will become increasingly insignificant compared to the expansion velocity as the universe expands if $a \propto t^{2 / 3}$.

  (iii) A distant cloud of intermingled hydrogen (H) atoms and carbon monoxide (CO) molecules has its redshift determined simultaneously in two ways: by detecting $21 \mathrm{~cm}$ radiation from atomic hydrogen and by detecting radiation from rotational transitions in CO molecules. The ratio of the $21 \mathrm{~cm}$ atomic transition frequency to the CO rotational transition frequency is proportional to $\alpha^{2}$, where $\alpha$ is the fine structure constant. It is suggested that there may be a small difference in the value of the constant $\alpha$ between the times of emission and reception of the radiation from the cloud.

  Show that the difference in the redshift values for the cloud, $\Delta z=z_{C O}-z_{21}$, determined separately by observations of the $\mathrm{H}$ and $\mathrm{CO}$ transitions, is related to $\delta \alpha=$ $\alpha_{r}-\alpha_{e}$, the difference in $\alpha$ values at the times of reception and emission, by

  $$\Delta z=2\left(\frac{\delta \alpha}{\alpha_{r}}\right)\left(1+z_{C O}\right)$$

  (iv) The universe today contains $30 \%$ of its total density in the form of pressureless matter and $70 \%$ in the form of a dark energy with constant redshift-independent density. If these are the only two significant constituents of the universe, show that their densities were equal when the scale factor of the universe was approximately equal to $75 \%$ of its present value.

  comment

Differential Geometry

• Paper 3, Section II, H

  Differential Geometry | Part II, 2013

  We say that a parametrization $\phi: U \rightarrow S \subset \mathbf{R}^{3}$ of a smooth surface $S$ is isothermal if the coefficients of the first fundamental form satisfy $F=0$ and $E=G=\lambda(u, v)^{2}$, for some smooth non-vanishing function $\lambda$ on $U$. For an isothermal parametrization, prove that

  $$\phi_{u u}+\phi_{v v}=2 \lambda^{2} H \mathbf{N}$$

  where $\mathbf{N}$ denotes the unit normal vector and $H$ the mean curvature, which you may assume is given by the formula

  $$H=\frac{g+e}{2 \lambda^{2}}$$

  where $g=-\left\langle\mathbf{N}_{u}, \phi_{u}\right\rangle$ and $e=-\left\langle\mathbf{N}_{v}, \phi_{v}\right\rangle$ are coefficients in the second fundamental form.

  Given a parametrization $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$ of a surface $S \subset \mathbf{R}^{3}$, we consider the complex valued functions on $U$ :

  $$\theta_{1}=x_{u}-i x_{v}, \quad \theta_{2}=y_{u}-i y_{v}, \quad \theta_{3}=z_{u}-i z_{v}$$

  Show that $\phi$ is isothermal if and only if $\theta_{1}^{2}+\theta_{2}^{2}+\theta_{3}^{2}=0$. If $\phi$ is isothermal, show that $S$ is a minimal surface if and only if $\theta_{1}, \theta_{2}, \theta_{3}$ are holomorphic functions of the complex variable $\zeta=u+i v$

  Consider the holomorphic functions on $D:=\mathbf{C} \backslash \mathbf{R}_{\geqslant 0}$ (with complex coordinate $\zeta=u+i v$ on $\mathbf{C})$ given by

  $$\theta_{1}:=\frac{1}{2}\left(1-\zeta^{-2}\right), \quad \theta_{2}:=-\frac{i}{2}\left(1+\zeta^{-2}\right), \quad \theta_{3}:=-\zeta^{-1}$$

  Find a smooth map $\phi(u, v)=(x(u, v), y(u, v), z(u, v)): D \rightarrow \mathbf{R}^{3}$ for which $\phi(-1,0)=\mathbf{0}$ and the $\theta_{i}$ defined by (2) satisfy the equations (1). Show furthermore that $\phi$ extends to a smooth map $\tilde{\phi}: \mathbf{C}^{*} \rightarrow \mathbf{R}^{3}$. If $w=x+i y$ is the complex coordinate on $\mathbf{C}$, show that

  $$\widetilde{\phi}(\exp (i w))=(\cosh y \cos x+1, \cosh y \sin x, y)$$

  comment

Dynamical Systems

• Paper 3, Section I, C

  Dynamical Systems | Part II, 2013

  A one-dimensional map is defined by

  $$x_{n+1}=F\left(x_{n}, \mu\right)$$

  where $\mu$ is a parameter. What is the condition for a bifurcation of a fixed point $x_{*}$ of $F$ ?

  Let $F(x, \mu)=x\left(x^{2}-2 x+\mu\right)$. Find the fixed points and show that bifurcations occur when $\mu=-1, \mu=1$ and $\mu=2$. Sketch the bifurcation diagram, showing the locus and stability of the fixed points in the $(x, \mu)$ plane and indicating the type of each bifurcation.

  comment

• Paper 3, Section II, C

  Dynamical Systems | Part II, 2013

  Let $f: I \rightarrow I$ be a continuous map of an interval $I \subset \mathbb{R}$. Explain what is meant by the statements (a) $f$ has a horseshoe and (b) $f$ is chaotic according to Glendinning's definition of chaos.

  Assume that $f$ has a 3-cycle $\left\{x_{0}, x_{1}, x_{2}\right\}$ with $x_{1}=f\left(x_{0}\right), x_{2}=f\left(x_{1}\right), x_{0}=f\left(x_{2}\right)$, $x_{0}<x_{1}<x_{2}$. Prove that $f^{2}$ has a horseshoe. [You may assume the Intermediate Value Theorem.]

  Represent the effect of $f$ on the intervals $I_{a}=\left[x_{0}, x_{1}\right]$ and $I_{b}=\left[x_{1}, x_{2}\right]$ by means of a directed graph. Explain how the existence of the 3 -cycle corresponds to this graph.

  The map $g: I \rightarrow I$ has a 4-cycle $\left\{x_{0}, x_{1}, x_{2}, x_{3}\right\}$ with $x_{1}=g\left(x_{0}\right), x_{2}=g\left(x_{1}\right)$, $x_{3}=g\left(x_{2}\right)$ and $x_{0}=g\left(x_{3}\right)$. If $x_{0}<x_{3}<x_{2}<x_{1}$ is $g$ necessarily chaotic? [You may use a suitable directed graph as part of your argument.]

  How does your answer change if $x_{0}<x_{2}<x_{1}<x_{3}$ ?

  comment

Electrodynamics

• Paper 3, Section II, 36B

  Electrodynamics | Part II, 2013

  (i) Obtain Maxwell's equations in empty space from the action functional

  $$S\left[A_{\mu}\right]=-\frac{1}{\mu_{0}} \int d^{4} x \frac{1}{4} F_{\mu \nu} F^{\mu \nu}$$

  where $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$.

  (ii) A modification of Maxwell's equations has the action functional

  $$\tilde{S}\left[A_{\mu}\right]=-\frac{1}{\mu_{0}} \int d^{4} x\left\{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+\frac{1}{2 \lambda^{2}} A_{\mu} A^{\mu}\right\},$$

  where again $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ and $\lambda$ is a constant. Obtain the equations of motion of this theory and show that they imply $\partial_{\mu} A^{\mu}=0$.

  (iii) Show that the equations of motion derived from $\tilde{S}$ admit solutions of the form

  $$A^{\mu}=A_{0}^{\mu} e^{i k_{\nu} x^{\nu}}$$

  where $A_{0}^{\mu}$ is a constant 4-vector, and the 4 -vector $k_{\mu}$ satisfies $A_{0}^{\mu} k_{\mu}=0$ and $k_{\mu} k^{\mu}=-1 / \lambda^{2}$.

  (iv) Show further that the tensor

  $$T_{\mu \nu}=\frac{1}{\mu_{0}}\left\{F_{\mu \sigma} F_{\nu}^{\sigma}-\frac{1}{4} \eta_{\mu \nu} F_{\alpha \beta} F^{\alpha \beta}-\frac{1}{2 \lambda^{2}}\left(\eta_{\mu \nu} A_{\alpha} A^{\alpha}-2 A_{\mu} A_{\nu}\right)\right\}$$

  is conserved, that is $\partial^{\mu} T_{\mu \nu}=0$.

  comment

Fluid Dynamics II

• Paper 3, Section II, A

  Fluid Dynamics II | Part II, 2013

  A disk hovers on a cushion of air above an air-table - a fine porous plate through which a constant flux of air is pumped. Let the disk have a radius $R$ and a weight $M g$ and hover at a low height $h \ll R$ above the air-table. Let the volume flux of air, which has density $\rho$ and viscosity $\mu$, be $w$ per unit surface area. The conditions are such that $\rho w h^{2} / \mu R \ll 1$. Explain the significance of this restriction.

  Find the pressure distribution in the air under the disk. Show that this pressure balances the weight of the disk if

  $$h=R\left(\frac{3 \pi \mu R w}{2 M g}\right)^{1 / 3}$$

  comment

Further Complex Methods

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2013

  Let a real-valued function $u=u(x, y)$ be the real part of a complex-valued function $f=f(z)$ which is analytic in the neighbourhood of a point $z=0$, where $z=x+i y .$ Derive a formula for $f$ in terms of $u$ and use it to find an analytic function $f$ whose real part is

  $$\frac{x^{3}+x^{2}-y^{2}+x y^{2}}{(x+1)^{2}+y^{2}}$$

  and such that $f(0)=0$.

  comment

Galois Theory

• Paper 3, Section II, I

  Galois Theory | Part II, 2013

  Let $p$ be a prime number and $F$ a field of characteristic $p$. Let $\operatorname{Fr}_{p}: F \rightarrow F$ be the Frobenius map defined by $\operatorname{Fr}_{p}(x)=x^{p}$ for all $x \in F$.

  (i) Prove that $\operatorname{Fr}_{p}$ is a field automorphism when $F$ is a finite field.

  (ii) Is the same true for an arbitrary algebraic extension $F$ of $\mathbb{F}_{p}$ ? Justify your answer.

  (iii) Let $F=\mathbb{F}_{p}\left(X_{1}, \ldots, X_{n}\right)$ be the rational function field in $n$ variables where $n \geqslant 1$ over $\mathbb{F}_{p}$. Determine the image of $\operatorname{Fr}_{p}: F \rightarrow F$, and show that $\operatorname{Fr}_{p}$ makes $F$ into an extension of degree $p^{n}$ over a subfield isomorphic to $F$. Is it a separable extension?

  comment

General Relativity

• Paper 3, Section II, D

  General Relativity | Part II, 2013

  The Schwarzschild metric for a spherically symmetric black hole is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where we have taken units in which we set $G=c=1$. Consider a photon moving within the equatorial plane $\theta=\frac{\pi}{2}$, along a path $x^{a}(\lambda)$ with affine parameter $\lambda$. Using a variational principle with Lagrangian

  $$L=g_{a b} \frac{d x^{a}}{d \lambda} \frac{d x^{b}}{d \lambda}$$

  or otherwise, show that

  $$\left(1-\frac{2 M}{r}\right)\left(\frac{d t}{d \lambda}\right)=E \quad \text { and } \quad r^{2}\left(\frac{d \phi}{d \lambda}\right)=h$$

  for constants $E$ and $h$. Deduce that

  $$\left(\frac{d r}{d \lambda}\right)^{2}=E^{2}-\frac{h^{2}}{r^{2}}\left(1-\frac{2 M}{r}\right)$$

  Assume now that the photon approaches from infinity. Show that the impact parameter (distance of closest approach) is given by

  $$b=\frac{h}{E}$$

  Denote the right hand side of equation $(*)$ as $f(r)$. By sketching $f(r)$ in each of the cases below, or otherwise, show that:

  (a) if $b^{2}>27 M^{2}$, the photon is deflected but not captured by the black hole;

  (b) if $b^{2}<27 M^{2}$, the photon is captured;

  (c) if $b^{2}=27 M^{2}$, the photon orbit has a particular form, which should be described.

  comment

Geometry and Groups

• Paper 3, Section I, $3 G$

  Geometry and Groups | Part II, 2013

  Let $\Lambda$ be a rank 2 lattice in the Euclidean plane. Show that the group $G$ of all Euclidean isometries of the plane that map $\Lambda$ onto itself is a discrete group. List the possible sizes of the point groups for $G$ and give examples to show that point groups of these sizes do arise.

  [You may quote any standard results without proof.]

  comment

Graph Theory

• Paper 3, Section II, F

  Graph Theory | Part II, 2013

  Let $G$ be a graph of order $n$ and average degree $d$. Let $A$ be the adjacency matrix of $G$ and let $x^{n}+c_{1} x^{n-1}+c_{2} x^{n-2}+\cdots+c_{n}$ be its characteristic polynomial. Show that $c_{1}=0$ and $c_{2}=-n d / 2$. Show also that $-c_{3}$ is twice the number of triangles in $G$.

  The eigenvalues of $A$ are $\lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{n}$. Prove that $\lambda_{1} \geqslant d$.

  Evaluate $\lambda_{1}+\cdots+\lambda_{n}$. Show that $\lambda_{1}^{2}+\cdots+\lambda_{n}^{2}=n d$ and infer that $\lambda_{1} \leqslant \sqrt{d(n-1)}$. Does there exist, for each $n$, a graph $G$ with $d>0$ for which $\lambda_{2}=\cdots=\lambda_{n}$ ?

  comment

Integrable Systems

• Paper 3, Section II, C

  Integrable Systems | Part II, 2013

  Let $U=U(x, y)$ and $V=V(x, y)$ be two $n \times n$ complex-valued matrix functions, smoothly differentiable in their variables. We wish to explore the solution of the overdetermined linear system

  $$\frac{\partial \mathbf{v}}{\partial y}=U(x, y) \mathbf{v}, \quad \frac{\partial \mathbf{v}}{\partial x}=V(x, y) \mathbf{v}$$

  for some twice smoothly differentiable vector function $\mathbf{v}(x, y)$.

  Prove that, if the overdetermined system holds, then the functions $U$ and $V$ obey the zero curvature representation

  $$\frac{\partial U}{\partial x}-\frac{\partial V}{\partial y}+U V-V U=0$$

  Let $u=u(x, y)$ and

  $$U=\left[\begin{array}{cc} i \lambda & i \bar{u} \\ i u & -i \lambda \end{array}\right], \quad V=\left[\begin{array}{cc} 2 i \lambda^{2}-i|u|^{2} & 2 i \lambda \bar{u}+\bar{u}_{y} \\ 2 i \lambda u-u_{y} & -2 i \lambda^{2}+i|u|^{2} \end{array}\right]$$

  where subscripts denote derivatives, $\bar{u}$ is the complex conjugate of $u$ and $\lambda$ is a constant. Find the compatibility condition on the function $u$ so that $U$ and $V$ obey the zero curvature representation.

  comment

Linear Analysis

• Paper 3, Section II, F

  Linear Analysis | Part II, 2013

  State the Stone-Weierstrass Theorem for real-valued functions.

  State Riesz's Lemma.

  Let $K$ be a compact, Hausdorff space and let $A$ be a subalgebra of $C(K)$ separating the points of $K$ and containing the constant functions. Fix two disjoint, non-empty, closed subsets $E$ and $F$ of $K$.

  (i) If $x \in E$ show that there exists $g \in A$ such that $g(x)=0,0 \leqslant g<1$ on $K$, and $g>0$ on $F$. Explain briefly why there is $M \in \mathbb{N}$ such that $g \geqslant \frac{2}{M}$ on $F$.

  (ii) Show that there is an open cover $U_{1}, U_{2}, \ldots, U_{m}$ of $E$, elements $g_{1}, g_{2}, \ldots, g_{m}$ of $A$ and positive integers $M_{1}, M_{2}, \ldots, M_{m}$ such that

  $$0 \leqslant g_{r}<1 \text { on } K, \quad g_{r} \geqslant \frac{2}{M_{r}} \text { on } F, \quad g_{r}<\frac{1}{2 M_{r}} \text { on } U_{r}$$

  for each $r=1,2, \ldots, m$.

  (iii) Using the inequality

  $$1-N t \leqslant(1-t)^{N} \leqslant \frac{1}{N t} \quad(0<t<1, N \in \mathbb{N})$$

  show that for sufficiently large positive integers $n_{1}, n_{2}, \ldots, n_{m}$, the element

  $$h_{r}=1-\left(1-g_{r}^{n_{r}}\right)^{M_{r}^{n_{r}}}$$

  of $A$ satisfies

  $$0 \leqslant h_{r} \leqslant 1 \text { on } K, \quad h_{r} \leqslant \frac{1}{4} \text { on } U_{r}, \quad h_{r} \geqslant\left(\frac{3}{4}\right)^{\frac{1}{m}} \text { on } F$$

  for each $r=1,2, \ldots, m$.

  (iv) Show that the element $h=h_{1} \cdot h_{2} \cdots \cdot h_{m}-\frac{1}{2}$ of $A$ satisfies

  $$-\frac{1}{2} \leqslant h \leqslant \frac{1}{2} \text { on } K, \quad h \leqslant-\frac{1}{4} \text { on } E, \quad h \geqslant \frac{1}{4} \text { on } F \text {. }$$

  Now let $f \in C(K)$ with $\|f\| \leqslant 1$. By considering the sets $\left\{x \in K: f(x) \leqslant-\frac{1}{4}\right\}$ and $\left\{x \in K: f(x) \geqslant \frac{1}{4}\right\}$, show that there exists $h \in A$ such that $\|f-h\| \leqslant \frac{3}{4}$. Deduce that $A$ is dense in $C(K)$.

  comment

Logic and Set Theory

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2013

  Explain carefully what is meant by syntactic entailment and semantic entailment in the propositional calculus. State the Completeness Theorem for the propositional calculus, and deduce the Compactness Theorem.

  Suppose $P, Q$ and $R$ are pairwise disjoint sets of primitive propositions, and let $\phi \in \mathcal{L}(P \cup Q)$ and $\psi \in \mathcal{L}(Q \cup R)$ be propositional formulae such that $(\phi \Rightarrow \psi)$ is a theorem of the propositional calculus. Consider the set

  $$X=\{\chi \in \mathcal{L}(Q) \mid \phi \vdash \chi\}$$

  Show that $X \cup\{\neg \psi\}$ is inconsistent, and deduce that there exists $\chi \in \mathcal{L}(Q)$ such that both $(\phi \Rightarrow \chi)$ and $(\chi \Rightarrow \psi)$ are theorems. [Hint: assuming $X \cup\{\neg \psi\}$ is consistent, take a suitable valuation $v$ of $Q \cup R$ and show that

  $$\{\phi\} \cup\{q \in Q \mid v(q)=1\} \cup\{\neg q \mid q \in Q, v(q)=0\}$$

  is inconsistent. The Deduction Theorem may be assumed without proof.]

  comment

Mathematical Biology

• Paper 3, Section I, A

  Mathematical Biology | Part II, 2013

  An immune system creates a burst of $N$ new white blood cells with probability $b$ per unit time. White blood cells die with probability $d$ each per unit time. Write down the master equation for $P_{n}(t)$, the probability that there are $n$ white blood cells at time $t$.

  Given that $n=n_{0}$ initially, find an expression for the mean of $n$.

  Show that the variance of $n$ has the form $A e^{-2 d t}+B e^{-d t}+C$ and find $A, B$ and $C$.

  If the immune system were modified to produce $k$ times as many cells per burst but with probability per unit time divided by a factor $k$, how would the mean and variance of the number of cells change?

  comment

• Paper 3, Section II, A

  Mathematical Biology | Part II, 2013

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} &\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}+u-u v+a u^{2} \\ &\frac{\partial v}{\partial t}=d \frac{\partial^{2} v}{\partial x^{2}}+u^{2}-b u v \end{aligned}$$

  where $a, b, d>0$.

  Find and sketch the range of $a, b$ for which the spatially homogeneous system has a stable stationary solution with $u>0$ and $v>0$.

  Considering spatial perturbations of the form $\cos (k x)$ about the solution found above, find conditions for the system to be unstable. Sketch this region in the $(d, b)$ plane for fixed $a \in(0,1)$.

  Find $k_{c}$, the critical wavenumber at the onset of the instability, in terms of $a$ and $b$.

  comment

Number Theory

• Paper 3, Section I, I

  Number Theory | Part II, 2013

  State the Chinese Remainder Theorem.

  A composite number $n$ is defined to be a Carmichael number if $b^{n-1} \equiv 1 \bmod n$ whenever $(b, n)=1$. Show that a composite $n$ is Carmichael if and only if $n$ is square-free and $(p-1)$ divides $(n-1)$ for all prime factors $p$ of $n$. [You may assume that, for $p$ an odd prime and $\alpha \geqslant 1$ an integer, $\left(\mathbb{Z} / p^{\alpha} \mathbb{Z}\right)^{\times}$is a cyclic group.]

  Show that if $n=(6 t+1)(12 t+1)(18 t+1)$ with all three factors prime, then $n$ is Carmichael.

  comment

• Paper 3, Section II, I

  Number Theory | Part II, 2013

  Define equivalence of binary quadratic forms and show that equivalent forms have the same discriminant.

  Show that an integer $n$ is properly represented by a binary quadratic form of discriminant $d$ if and only if $x^{2} \equiv d \bmod 4 n$ is soluble in integers. Which primes are represented by a form of discriminant $-20$ ?

  What does it mean for a positive definite form to be reduced? Find all reduced forms of discriminant $-20$. For each member of your list find the primes less than 100 represented by the form.

  comment

Numerical Analysis

• Paper 3, Section II, C

  Numerical Analysis | Part II, 2013

  (i) Suppose that $A$ is a real $n \times n$ matrix, and that $\mathbf{w} \in \mathbb{R}^{n}$ and $\lambda_{1} \in \mathbb{R}$ are given so that $A \mathbf{w}=\lambda_{1} \mathbf{w}$. Further, let $S$ be a non-singular matrix such that $S \mathbf{w}=c \mathbf{e}_{1}$, where $\mathbf{e}_{1}$ is the first coordinate vector and $c \neq 0$. Let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are $\lambda_{1}$ together with the eigenvalues of the bottom right $(n-1) \times(n-1)$ submatrix of $\widehat{A}$.

  (ii) Suppose again that $A$ is a real $n \times n$ matrix, and that two linearly independent vectors $\mathbf{v}, \mathbf{w} \in \mathbb{R}^{n}$ are given such that the linear subspace $\mathcal{L}\{\mathbf{v}, \mathbf{w}\}$ spanned by $\mathbf{v}$ and $w$ is invariant under the action of $A$, that is

  $$x \in \mathcal{L}\{\mathbf{v}, \mathbf{w}\} \quad \Rightarrow \quad A x \in \mathcal{L}\{\mathbf{v}, \mathbf{w}\} .$$

  Denote by $V$ an $n \times 2$ matrix whose two columns are the vectors $\mathbf{v}$ and $\mathbf{w}$, and let $S$ be a non-singular matrix such that $R=S V$ is upper triangular, that is

  $$R=S V=S \times\left(\begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \\ \vdots & \vdots \\ v_{n} & w_{n} \end{array}\right)=\left(\begin{array}{cc} r_{11} & r_{12} \\ 0 & r_{22} \\ 0 & 0 \\ \vdots & \vdots \\ 0 & 0 \end{array}\right)$$

  Again, let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are the eigenvalues of the top left $2 \times 2$ submatrix of $\widehat{A}$together with the eigenvalues of the bottom right $(n-2) \times(n-2)$ submatrix of $\widehat{A} .$

  comment

Optimization and Control

• Paper 3, Section II, K

  Optimization and Control | Part II, 2013

  A particle follows a discrete-time trajectory in $\mathbb{R}^{2}$ given by

  $$\left(\begin{array}{l} x_{t+1} \\ y_{t+1} \end{array}\right)=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)\left(\begin{array}{l} x_{t} \\ y_{t} \end{array}\right)+\left(\begin{array}{c} t \\ 1 \end{array}\right) u_{t}+\left(\begin{array}{c} \epsilon_{t} \\ 0 \end{array}\right)$$

  where $\left\{\epsilon_{t}\right\}$ is a white noise sequence with $E \epsilon_{t}=0$ and $E \epsilon_{t}^{2}=v$. Given $\left(x_{0}, y_{0}\right)$, we wish to choose $\left\{u_{t}\right\}_{t=0}^{9}$ to minimize $C=E\left[x_{10}^{2}+\sum_{t=0}^{9} u_{t}^{2}\right]$.

  Show that for some $\left\{a_{t}\right\}$ this problem can be reduced to one of controlling a scalar state $\xi_{t}=x_{t}+a_{t} y_{t}$.

  Find, in terms of $x_{0}, y_{0}$, the optimal $u_{0}$. What is the change in minimum $C$ achievable when the system starts in $\left(x_{0}, y_{0}\right)$ as compared to when it starts in $(0,0)$ ?

  Consider now a trajectory starting at $\left(x_{-1}, y_{-1}\right)=(11,-1)$. What value of $u_{-1}$ is optimal if we wish to minimize $5 u_{-1}^{2}+C$ ?

  comment

Partial Differential Equations

• Paper 3, Section II, C

  Partial Differential Equations | Part II, 2013

  Define the parabolic boundary $\partial_{p a r} \Omega_{T}$ of the domain $\Omega_{T}=[0,1] \times(0, T]$ for $T>0$.

  Let $u=u(x, t)$ be a smooth real-valued function on $\Omega_{T}$ which satisfies the inequality

  $$u_{t}-a u_{x x}+b u_{x}+c u \leqslant 0$$

  Assume that the coefficients $a, b$ and $c$ are smooth functions and that there exist positive constants $m, M$ such that $m \leqslant a \leqslant M$ everywhere, and $c \geqslant 0$. Prove that

  $$\max _{(x, t) \in \bar{\Omega}_{T}} u(x, t) \leqslant \max _{(x, t) \in \partial_{\text {par }} \Omega_{T}} u^{+}(x, t) .$$

  [Here $u^{+}=\max \{u, 0\}$ is the positive part of the function $u$.]

  Consider a smooth real-valued function $\phi$ on $\Omega_{T}$ such that

  $$\phi_{t}-\phi_{x x}-\left(1-\phi^{2}\right) \phi=0, \quad \phi(x, 0)=f(x)$$

  everywhere, and $\phi(0, t)=1=\phi(1, t)$ for all $t \geqslant 0$. Deduce from $(*)$ that if $f(x) \leqslant 1$ for all $x \in[0,1]$ then $\phi(x, t) \leqslant 1$ for all $(x, t) \in \Omega_{T}$. [Hint: Consider $u=\phi^{2}-1$ and compute $\left.u_{t}-u_{x x} \cdot\right]$

  comment

Principles of Quantum Mechanics

• Paper 3, Section II, E

  Principles of Quantum Mechanics | Part II, 2013

  A particle moves in one dimension in an infinite square-well potential $V(x)=0$ for $|x|<a$ and $\infty$ for $|x|>a$. Find the energy eigenstates. Show that the energy eigenvalues are given by $E_{n}=E_{1} n^{2}$ for integer $n$, where $E_{1}$ is a constant which you should find.

  The system is perturbed by the potential $\delta V=\epsilon x / a$. Show that the energy of the $n^{\text {th }}$level $E_{n}$ remains unchanged to first order in $\epsilon$. Show that the ground-state wavefunction is

  $$\psi_{1}(x)=\frac{1}{\sqrt{a}}\left[\cos \frac{\pi x}{2 a}+\frac{D \epsilon}{\pi^{2} E_{1}} \sum_{n=2,4, \ldots}(-1)^{A n} \frac{n^{B}}{\left(n^{2}-1\right)^{C}} \sin \frac{n \pi x}{2 a}+\mathcal{O}\left(\epsilon^{2}\right)\right]$$

  where $A, B, C$ and $D$ are numerical constants which you should find. Briefly comment on the conservation of parity in the unperturbed and perturbed systems.

  comment

Principles of Statistics

• Paper 3, Section II, K

  Principles of Statistics | Part II, 2013

  What is meant by a convex decision problem? State and prove a theorem to the effect that, in a convex decision problem, there is no point in randomising. [You may use standard terms without defining them.]

  The sample space, parameter space and action space are each the two-point set $\{1,2\}$. The observable $X$ takes value 1 with probability $2 / 3$ when the parameter $\Theta=1$, and with probability $3 / 4$ when $\Theta=2$. The loss function $L(\theta, a)$ is 0 if $a=\theta$, otherwise 1 . Describe all the non-randomised decision rules, compute their risk functions, and plot these as points in the unit square. Identify an inadmissible non-randomised decision rule, and a decision rule that dominates it.

  Show that the minimax rule has risk function $(8 / 17,8 / 17)$, and is Bayes against a prior distribution that you should specify. What is its Bayes risk? Would a Bayesian with this prior distribution be bound to use the minimax rule?

  comment

Probability and Measure

• Paper 3, Section II, $25 K$

  Probability and Measure | Part II, 2013

  Let $X$ be an integrable random variable with $\mathbb{E}(X)=0$. Show that the characteristic function $\phi_{X}$ is differentiable with $\phi_{X}^{\prime}(0)=0$. [You may use without proof standard convergence results for integrals provided you state them clearly.]

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables, all having the same distribution as $X$. Set $S_{n}=X_{1}+\cdots+X_{n}$. Show that $S_{n} / n \rightarrow 0$ in distribution. Deduce that $S_{n} / n \rightarrow 0$ in probability. [You may not use the Strong Law of Large Numbers.]

  comment

Representation Theory

• Paper 3, Section II, G

  Representation Theory | Part II, 2013

  Suppose that $\left(\rho_{1}, V_{1}\right)$ and $\left(\rho_{2}, V_{2}\right)$ are complex representations of the finite groups $G_{1}$ and $G_{2}$ respectively. Use $\rho_{1}$ and $\rho_{2}$ to construct a representation $\rho_{1} \otimes \rho_{2}$ of $G_{1} \times G_{2}$ on $V_{1} \otimes V_{2}$ and show that its character satisfies

  $$\chi \rho_{1} \otimes \rho_{2}\left(g_{1}, g_{2}\right)=\chi_{\rho_{1}}\left(g_{1}\right) \chi \rho_{2}\left(g_{2}\right)$$

  for each $g_{1} \in G_{1}, g_{2} \in G_{2}$.

  Prove that if $\rho_{1}$ and $\rho_{2}$ are irreducible then $\rho_{1} \otimes \rho_{2}$ is irreducible as a representation of $G_{1} \times G_{2}$. Moreover, show that every irreducible complex representation of $G_{1} \times G_{2}$ arises in this way.

  Is it true that every complex representation of $G_{1} \times G_{2}$ is of the form $\rho_{1} \otimes \rho_{2}$ with $\rho_{i}$ a complex representation of $G_{i}$ for $i=1,2 ?$ Justify your answer.

  comment

Riemann Surfaces

• Paper 3, Section II, I

  Riemann Surfaces | Part II, 2013

  Let $\Lambda=\mathbb{Z}+\mathbb{Z} \lambda$ be a lattice in $\mathbb{C}$ where $\operatorname{Im}(\lambda)>0$, and let $X$ be the complex torus $\mathbb{C} / \Lambda .$

  (i) Give the definition of an elliptic function with respect to $\Lambda$. Show that there is a bijection between the set of elliptic functions with respect to $\Lambda$ and the set of holomorphic maps from $X$ to the Riemann sphere. Next, show that if $f$ is an elliptic function with respect to $\Lambda$ and $f^{-1}\{\infty\}=\emptyset$, then $f$ is constant.

  (ii) Assume that

  $$f(z)=\frac{1}{z^{2}}+\sum_{\omega \in \Lambda \backslash\{0\}}\left(\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}}\right)$$

  defines a meromorphic function on $\mathbb{C}$, where the sum converges uniformly on compact subsets of $\mathbb{C} \backslash \Lambda$. Show that $f$ is an elliptic function with respect to $\Lambda$. Calculate the order of $f$.

  Let $g$ be an elliptic function with respect to $\Lambda$ on $\mathbb{C}$, which is holomorphic on $\mathbb{C} \backslash \Lambda$ and whose only zeroes in the closed parallelogram with vertices $\{0,1, \lambda, \lambda+1\}$ are simple zeroes at the points $\left\{\frac{1}{2}, \frac{\lambda}{2}, \frac{1}{2}+\frac{\lambda}{2}\right\}$. Show that $g$ is a non-zero constant multiple of $f^{\prime}$.

  comment

Statistical Modelling

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2013

  Consider the linear model $Y=X \beta+\epsilon$ where $Y=\left(Y_{1}, \ldots, Y_{n}\right)^{\mathrm{T}}, \beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{\mathrm{T}}$, and $\epsilon=\left(\epsilon_{1}, \ldots, \epsilon_{n}\right)^{\mathrm{T}}$, with $\epsilon_{1}, \ldots, \epsilon_{n}$ independent $N\left(0, \sigma^{2}\right)$ random variables. The $(n \times p)$ matrix $X$ is known and is of full rank $p<n$. Give expressions for the maximum likelihood estimators $\widehat{\beta}$ and $\widehat{\sigma}^{2}$ of $\beta$ and $\sigma^{2}$ respectively, and state their joint distribution. Show that $\widehat{\beta}$ is unbiased whereas $\widehat{\sigma}^{2}$ is biased.

  Suppose that a new variable $Y^{*}$ is to be observed, satisfying the relationship

  $$Y^{*}=x^{* \mathrm{~T}} \beta+\epsilon^{*}$$

  where $x^{*}(p \times 1)$ is known, and $\epsilon^{*} \sim N\left(0, \sigma^{2}\right)$ independently of $\epsilon$. We propose to predict $Y^{*}$ by $\widetilde{Y}=x^{* \mathrm{~T}} \widehat{\beta}$. Identify the distribution of

  $$\frac{Y^{*}-\tilde{Y}}{\tau \tilde{\sigma}}$$

  where

  $$\begin{aligned} \tilde{\sigma}^{2} &=\frac{n}{n-p} \widehat{\sigma}^{2} \\ \tau^{2} &=x^{* \mathrm{~T}}\left(X^{\mathrm{T}} X\right)^{-1} x^{*}+1 \end{aligned}$$

  comment

Statistical Physics

• Paper 3, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) Briefly describe the microcanonical ensemble.

  (ii) For quantum mechanical systems the energy levels are discrete. Explain why we can write the probability distribution in this case as

  $$p\left(\left\{n_{i}\right\}\right)= \begin{cases}\text { const }>0 & \text { for } E \leqslant E\left(\left\{n_{i}\right\}\right)<E+\Delta E \\ 0 & \text { otherwise }\end{cases}$$

  What assumption do we make for the energy interval $\Delta E$ ?

  Consider $N$ independent linear harmonic oscillators of equal frequency $\omega$. Their total energy is given by

  $$E\left(\left\{n_{i}\right\}\right)=\sum_{i=1}^{N} \hbar \omega\left(n_{i}+\frac{1}{2}\right)=M \hbar \omega+\frac{N}{2} \hbar \omega \quad \text { with } \quad M=\sum_{i=1}^{N} n_{i}$$

  Here $n_{i}=0,1,2, \ldots$ is the excitation number of oscillator $i$.

  (iii) Show that, for fixed $N$ and $M$, the number $g_{N}(M)$ of possibilities to distribute the $M$ excitations over $N$ oscillators (i.e. the number of different choices $\left\{n_{i}\right\}$ consistent with $M$ ) is given by

  $$g_{N}(M)=\frac{(M+N-1) !}{M !(N-1) !}$$

  [Hint: You may wish to consider the set of $N$ oscillators plus $M-1$ "additional" excitations and what it means to choose $M$ objects from this set.]

  (iv) Using the probability distribution of part (ii), calculate the probability distribution $p\left(E_{1}\right)$ for the "first" oscillator as a function of its energy $E_{1}=n_{1} \hbar \omega+\frac{1}{2} \hbar \omega$.

  (v) If $\Delta E=\hbar \omega \ll E$ then exactly one value of $M$ will correspond to a total energy inside the interval $(E, E+\Delta E)$. In this case, show that

  $$p\left(E_{1}\right) \approx \frac{g_{N-1}\left(M-n_{1}\right)}{g_{N}(M)} .$$

  Approximate this result in the limit $N \gg 1, M \gg n_{1}$.

  comment

Stochastic Financial Models

• Paper 3, Section II, J

  Stochastic Financial Models | Part II, 2013

  Suppose that $\left(\varepsilon_{t}\right)_{t=0,1, \ldots, T}$ is a sequence of independent and identically distributed random variables such that $E \exp \left(z \varepsilon_{1}\right)<\infty$ for all $z \in \mathbb{R}$. Each day, an agent receives an income, the income on day $t$ being $\varepsilon_{t}$. After receiving this income, his wealth is $w_{t}$. From this wealth, he chooses to consume $c_{t}$, and invests the remainder $w_{t}-c_{t}$ in a bank account which pays a daily interest rate of $r>0$. Write down the equation for the evolution of $w_{t}$.

  Suppose we are given constants $\beta \in(0,1), A_{T}, \gamma>0$, and define the functions

  $$U(x)=-\exp (-\gamma x), \quad U_{T}(x)=-A_{T} \exp (-\nu x)$$

  where $\nu:=\gamma r /(1+r)$. The agent's objective is to attain

  $$V_{0}(w):=\sup E\left\{\sum_{t=0}^{T-1} \beta^{t} U\left(c_{t}\right)+\beta^{T} U_{T}\left(w_{T}\right) \mid w_{0}=w\right\},$$

  where the supremum is taken over all adapted sequences $\left(c_{t}\right)$. If the value function is defined for $0 \leqslant n<T$ by

  $$V_{n}(w)=\sup E\left\{\sum_{t=n}^{T-1} \beta^{t-n} U\left(c_{t}\right)+\beta^{T-n} U_{T}\left(w_{T}\right) \mid w_{n}=w\right\}$$

  with $V_{T}=U_{T}$, explain briefly why you expect the $V_{n}$ to satisfy

  $$V_{n}(w)=\sup _{c}\left[U(c)+\beta E\left\{V_{n+1}\left((1+r)(w-c)+\varepsilon_{n+1}\right)\right\}\right]$$

  Show that the solution to $(*)$ has the form

  $$V_{n}(w)=-A_{n} \exp (-\nu w),$$

  for constants $A_{n}$ to be identified. What is the form of the consumption choices that achieve the supremum in $(*)$ ?

  comment

Topics in Analysis

• Paper 3, Section I, $2 F$

  Topics in Analysis | Part II, 2013

  State Brouwer's fixed point theorem. Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ be a continuous function with the property that $|f(x)-x| \leqslant 1$ for all $x$. Show that $f$ is surjective.

  comment

• Paper 3, Section II, F

  Topics in Analysis | Part II, 2013

  Suppose that $x_{0}, x_{1}, \ldots, x_{n} \in[-1,1]$ are distinct points. Let $f$ be an infinitely differentiable real-valued function on an open interval containing $[-1,1]$. Let $p$ be the unique polynomial of degree at most $n$ such that $f\left(x_{r}\right)=p\left(x_{r}\right)$ for $r=0,1, \ldots, n$. Show that for each $x \in[-1,1]$ there is some $\xi \in(-1,1)$ such that

  $$f(x)-p(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right) \ldots\left(x-x_{n}\right)$$

  Now take $x_{r}=\cos \frac{2 r+1}{2 n+2} \pi$. Show that

  $$|f(x)-p(x)| \leqslant \frac{1}{2^{n}(n+1) !} \sup _{\xi \in[-1,1]}\left|f^{(n+1)}(\xi)\right|$$

  for all $x \in[-1,1]$. Deduce that there is a polynomial $p$ of degree at most $n$ such that

  $$\left|\frac{1}{3+x}-p(x)\right| \leqslant \frac{1}{4^{n+1}}$$

  for all $x \in[-1,1]$.

  comment

Waves

• Paper 3, Section II, C

  Waves | Part II, 2013

  The dispersion relation for sound waves of frequency $\omega$ in a stationary homogeneous gas is $\omega=c_{0}|\mathbf{k}|$, where $c_{0}$ is the speed of sound and $\mathbf{k}$ is the wavenumber. Derive the dispersion relation for sound waves of frequency $\omega$ in a uniform flow with velocity U.

  For a slowly-varying medium with local dispersion relation $\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$, derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  explaining carefully the meaning of the notation used.

  Suppose that two-dimensional sound waves with initial wavenumber $\left(k_{0}, l_{0}, 0\right)$ are generated at the origin in a gas occupying the half-space $y>0$. If the gas has a slowlyvarying mean velocity $(\gamma y, 0,0)$, where $\gamma>0$, show:

  (a) that if $k_{0}>0$ and $l_{0}>0$ the waves reach a maximum height (which should be identified), and then return to the level $y=0$ in a finite time;

  (b) that if $k_{0}<0$ and $l_{0}>0$ then there is no bound on the height to which the waves propagate.

  Comment briefly on the existence, or otherwise, of a quiet zone.

  comment