Part II, 2013

Algebraic Geometry

• Paper 1, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $V \subset \mathbb{A}^{n}$ be an affine variety over an algebraically closed field $k$. What does it mean to say that $V$ is irreducible? Show that any non-empty affine variety $V \subset \mathbb{A}^{n}$ is the union of a finite number of irreducible affine varieties $V_{j} \subset \mathbb{A}^{n}$.

  Define the ideal $I(V)$ of $V$. Show that $I(V)$ is a prime ideal if and only if $V$ is irreducible.

  Assume that the base field $k$ has characteristic zero. Determine the irreducible components of

  $$V\left(X_{1} X_{2}, X_{1} X_{3}+X_{2}^{2}-1, X_{1}^{2}\left(X_{1}-X_{3}\right)\right) \subset \mathbb{A}^{3}$$

  comment

• Paper 2, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $V \subset \mathbb{P}^{3}$ be an irreducible quadric surface.

  (i) Show that if $V$ is singular, then every nonsingular point lies in exactly one line in $V$, and that all the lines meet in the singular point, which is unique.

  (ii) Show that if $V$ is nonsingular then each point of $V$ lies on exactly two lines of $V$.

  Let $V$ be nonsingular, $P_{0}$ a point of $V$, and $\Pi \subset \mathbb{P}^{3}$ a plane not containing $P_{0}$. Show that the projection from $P_{0}$ to $\Pi$ is a birational map $f: V \rightarrow \rightarrow \Pi$. At what points does $f$ fail to be regular? At what points does $f^{-1}$ fail to be regular? Justify your answers.

  comment

• Paper 3, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $C \subset \mathbb{P}^{2}$ be the plane curve given by the polynomial

  $$X_{0}^{n}-X_{1}^{n}-X_{2}^{n}$$

  over the field of complex numbers, where $n \geqslant 3$.

  (i) Show that $C$ is nonsingular.

  (ii) Compute the divisors of the rational functions

  $$x=\frac{X_{1}}{X_{0}}, \quad y=\frac{X_{2}}{X_{0}}$$

  on $C$.

  (iii) Consider the morphism $\phi=\left(X_{0}: X_{1}\right): C \rightarrow \mathbb{P}^{1}$. Compute its ramification points and degree.

  (iv) Show that a basis for the space of regular differentials on $C$ is

  $$\left\{x^{i} y^{j} \omega_{0} \mid i, j \geqslant 0, i+j \leqslant n-3\right\}$$

  where $\omega_{0}=d x / y^{n-1} .$

  comment

• Paper 4, Section II, H

  Algebraic Geometry | Part II, 2013

  Let $C$ be a nonsingular projective curve, and $D$ a divisor on $C$ of degree $d$.

  (i) State the Riemann-Roch theorem for $D$, giving a brief explanation of each term. Deduce that if $d>2 g-2$ then $\ell(D)=1-g+d$.

  (ii) Show that, for every $P \in C$,

  $$\ell(D-P) \geqslant \ell(D)-1$$

  Deduce that $\ell(D) \leqslant 1+d$. Show also that if $\ell(D)>1$, then $\ell(D-P)=\ell(D)-1$ for all but finitely many $P \in C$.

  (iii) Deduce that for every $d \geqslant g-1$ there exists a divisor $D$ of degree $d$ with $\ell(D)=1-g+d$.

  comment

Algebraic Topology

• Paper 1, Section II, 21G

  Algebraic Topology | Part II, 2013

  (i) Define the notion of the fundamental group $\pi_{1}\left(X, x_{0}\right)$ of a path-connected space $X$ with base point $x_{0}$.

  (ii) Prove that if a group $G$ acts freely and properly discontinuously on a simply connected space $Z$, then $\pi_{1}\left(G \backslash Z, x_{0}\right)$ is isomorphic to $G$. [You may assume the homotopy lifting property, provided that you state it clearly.]

  (iii) Suppose that $p, q$ are distinct points on the 2 -sphere $S^{2}$ and that $X=S^{2} /(p \sim q)$. Exhibit a simply connected space $Z$ with an action of a group $G$ as in (ii) such that $X=G \backslash Z$, and calculate $\pi_{1}\left(X, x_{0}\right)$.

  comment

• Paper 2, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State the Seifert-van Kampen theorem.

  (ii) Assuming any standard results about the fundamental group of a circle that you wish, calculate the fundamental group of the $n$-sphere, for every $n \geqslant 2$.

  (iii) Suppose that $n \geqslant 3$ and that $X$ is a path-connected topological $n$-manifold. Show that $\pi_{1}\left(X, x_{0}\right)$ is isomorphic to $\pi_{1}\left(X-\{P\}, x_{0}\right)$ for any $P \in X-\left\{x_{0}\right\}$.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Mayer-Vietoris theorem for the homology groups of polyhedra.

  (ii) Calculate the homology groups of the $n$-sphere, for every $n \geqslant 0$.

  (iii) Suppose that $a \geqslant 1$ and $b \geqslant 0$. Calculate the homology groups of the subspace $X$ of $\mathbb{R}^{a+b}$ defined by $\sum_{i=1}^{a} x_{i}^{2}-\sum_{j=a+1}^{a+b} x_{j}^{2}=1$.

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Lefschetz fixed point theorem.

  (ii) Show that if $n$ is even, then for every map $f: S^{n} \rightarrow S^{n}$ there is a point $x \in S^{n}$ such that $f(x)=\pm x$. Is this true if $n$ is odd? [Standard results on the homology groups for the $n$-sphere may be assumed without proof, provided they are stated clearly.]

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  Consider a quantum system with Hamiltonian $\widehat{H}$and energy levels

  $$E_{0}<E_{1}<E_{2}<\ldots$$

  For any state $|\psi\rangle$ define the Rayleigh-Ritz quotient $R[\psi]$ and show the following:

  (i) the ground state energy $E_{0}$ is the minimum value of $R[\psi]$;

  (ii) all energy eigenstates are stationary points of $R[\psi]$ with respect to variations of $|\psi\rangle$.

  Under what conditions can the value of $R\left[\psi_{\alpha}\right]$ for a trial wavefunction $\psi_{\alpha}$ (depending on some parameter $\alpha$ ) be used as an estimate of the energy $E_{1}$ of the first excited state? Explain your answer.

  For a suitably chosen trial wavefunction which is the product of a polynomial and a Gaussian, use the Rayleigh-Ritz quotient to estimate $E_{1}$ for a particle of mass $m$ moving in a potential $V(x)=g|x|$, where $g$ is a constant.

  [You may use the integral formulae,

  $$\begin{aligned} \int_{0}^{\infty} x^{2 n} \exp \left(-p x^{2}\right) d x &=\frac{(2 n-1) ! !}{2(2 p)^{n}} \sqrt{\frac{\pi}{p}} \\ \int_{0}^{\infty} x^{2 n+1} \exp \left(-p x^{2}\right) d x &=\frac{n !}{2 p^{n+1}} \end{aligned}$$

  where $n$ is a non-negative integer and $p$ is a constant. ]

  comment

• Paper 2, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  (i) A particle of momentum $\hbar k$ and energy $E=\hbar^{2} k^{2} / 2 m$ scatters off a sphericallysymmetric target in three dimensions. Define the corresponding scattering amplitude $f$ as a function of the scattering angle $\theta$. Expand the scattering amplitude in partial waves of definite angular momentum $l$, and determine the coefficients of this expansion in terms of the phase shifts $\delta_{l}(k)$ appearing in the following asymptotic form of the wavefunction, valid at large distance from the target,

  $$\psi(\mathbf{r}) \sim \sum_{l=0}^{\infty} \frac{2 l+1}{2 i k}\left[e^{2 i \delta_{l}} \frac{e^{i k r}}{r}-(-1)^{l} \frac{e^{-i k r}}{r}\right] P_{l}(\cos \theta) .$$

  Here, $r=|\mathbf{r}|$ is the distance from the target and $P_{l}$ are the Legendre polynomials.

  [You may use without derivation the following approximate relation between plane and spherical waves (valid asymptotically for large $r$ ):

  $$\exp (i k z) \sim \sum_{l=0}^{\infty}(2 l+1) i^{l} \frac{\sin \left(k r-\frac{1}{2} l \pi\right)}{k r} P_{l}(\cos \theta) .$$

  (ii) Suppose that the potential energy takes the form $V(r)=\lambda U(r)$ where $\lambda \ll 1$ is a dimensionless coupling. By expanding the wavefunction in a power series in $\lambda$, derive the Born Approximation to the scattering amplitude in the form

  $$f(\theta)=-\frac{2 m \lambda}{\hbar^{2}} \int_{0}^{\infty} U(r) \frac{\sin q r}{q} r d r$$

  up to corrections of order $\lambda^{2}$, where $q=2 k \sin (\theta / 2)$. [You may quote any results you need for the Green's function for the differential operator $\nabla^{2}+k^{2}$ provided they are stated clearly.]

  (iii) Derive the corresponding order $\lambda$ contribution to the phase shift $\delta_{l}(k)$ of angular momentum $l$.

  [You may use the orthogonality relations

  $$\int_{-1}^{+1} P_{l}(w) P_{m}(w) d w=\frac{2}{(2 l+1)} \delta_{l m}$$

  and the integral formula

  $$\int_{0}^{1} P_{l}\left(1-2 x^{2}\right) \sin (a x) d x=\frac{a}{2}\left[j_{l}\left(\frac{a}{2}\right)\right]^{2}$$

  where $j_{l}(z)$ is a spherical Bessel function.]

  comment

• Paper 3, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  Write down the classical Hamiltonian for a particle of mass $m$, electric charge $-e$ and momentum p moving in the background of an electromagnetic field with vector and scalar potentials $\mathbf{A}(\mathbf{x}, t)$ and $\phi(\mathbf{x}, t)$.

  Consider the case of a constant uniform magnetic field, $\mathbf{B}=(0,0, B)$ and $\mathbf{E}=0$. Working in the gauge with $\mathbf{A}=(-B y, 0,0)$ and $\phi=0$, show that Hamilton's equations,

  $$\dot{\mathbf{x}}=\frac{\partial H}{\partial \mathbf{p}}, \quad \dot{\mathbf{p}}=-\frac{\partial H}{\partial \mathbf{x}},$$

  admit solutions corresponding to circular motion in the $x-y$ plane with angular frequency $\omega_{B}=e B / m$.

  Show that, in the same gauge, the coordinates $\left(x_{0}, y_{0}, 0\right)$ of the centre of the circle are related to the instantaneous position $\mathbf{x}=(x, y, z)$ and momentum $\mathbf{p}=\left(p_{x}, p_{y}, p_{z}\right)$ of the particle by

  $$x_{0}=x-\frac{p_{y}}{e B}, \quad y_{0}=\frac{p_{x}}{e B} .$$

  Write down the quantum Hamiltonian $\hat{H}$ for the system. In the case of a uniform constant magnetic field discussed above, find the allowed energy levels. Working in the gauge specified above, write down quantum operators corresponding to the classical quantities $x_{0}$ and $y_{0}$ defined in (1) above and show that they are conserved.

  [In this question you may use without derivation any facts relating to the energy spectrum of the quantum harmonic oscillator provided they are stated clearly.]

  comment

• Paper 4, Section II, D

  Applications of Quantum Mechanics | Part II, 2013

  Define the Floquet matrix for a particle moving in a periodic potential in one dimension and explain how it determines the allowed energy bands of the system.

  A potential barrier in one dimension has the form

  $$V(x)= \begin{cases}V_{0}(x), & |x|<a / 4 \\ 0, & |x|>a / 4\end{cases}$$

  where $V_{0}(x)$ is a smooth, positive function of $x$. The reflection and transmission amplitudes for a particle of wavenumber $k>0$, incident from the left, are $r(k)$ and $t(k)$ respectively. For a particle of wavenumber $-k$, incident from the right, the corresponding amplitudes are $r^{\prime}(k)$ and $t^{\prime}(k)=t(k)$. In the following, for brevity, we will suppress the $k$-dependence of these quantities.

  Consider the periodic potential $\tilde{V}$, defined by $\tilde{V}(x)=V(x)$ for $|x|<a / 2$ and by $\tilde{V}(x+a)=\widetilde{V}(x)$ elsewhere. Write down two linearly independent solutions of the corresponding Schrödinger equation in the region $-3 a / 4<x<-a / 4$. Using the scattering data given above, extend these solutions to the region $a / 4<x<3 a / 4$. Hence find the Floquet matrix of the system in terms of the amplitudes $r, r^{\prime}$ and $t$ defined above.

  Show that the edges of the allowed energy bands for this potential lie at $E=\hbar^{2} k^{2} / 2 m$, where

  $$k a=i \log \left(t \pm \sqrt{r r^{\prime}}\right)$$

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2013

  Let $\left(X_{t}, t \geqslant 0\right)$ be a Markov chain on $\{0,1, \ldots\}$ with $Q$-matrix given by

  $$\begin{aligned} q_{n, n+1} &=\lambda_{n} \\ q_{n, 0} &=\lambda_{n} \varepsilon_{n} \quad(n>0) \\ q_{n, m} &=0 \quad \text { if } m \notin\{0, n, n+1\} \end{aligned}$$

  where $\varepsilon_{n}, \lambda_{n}>0$.

  (i) Show that $X$ is transient if and only if $\sum_{n} \varepsilon_{n}<\infty$. [You may assume without proof that $x(1-\delta) \leqslant \log (1+x) \leqslant x$ for all $\delta>0$ and all sufficiently small positive $x$.]

  (ii) Assume that $\sum_{n} \varepsilon_{n}<\infty$. Find a necessary and sufficient condition for $X$ to be almost surely explosive. [You may assume without proof standard results about pure birth processes, provided that they are stated clearly.]

  (iii) Find a stationary measure for $X$. For the case $\lambda_{n}=\lambda$ and $\varepsilon_{n}=\alpha /(n+1)(\lambda, \alpha>0)$, show that $X$ is positive recurrent if and only if $\alpha>1$.

  comment

• Paper 2, Section II, J

  Applied Probability | Part II, 2013

  (i) Define a Poisson process as a Markov chain on the non-negative integers and state three other characterisations.

  (ii) Let $\lambda(s)(s \geqslant 0)$ be a continuous positive function. Let $\left(X_{t}, t \geqslant 0\right)$ be a right-continuous process with independent increments, such that

  $$\begin{aligned} \mathbb{P}\left(X_{t+h}=X_{t}+1\right) &=\lambda(t) h+o(h) \\ \mathbb{P}\left(X_{t+h}=X_{t}\right) &=1-\lambda(t) h+o(h) \end{aligned}$$

  where the $o(h)$ terms are uniform in $t \in[0, \infty)$. Show that $X_{t}$ is a Poisson random variable with parameter $\Lambda(t)=\int_{0}^{t} \lambda(s) d s$.

  (iii) Let $X=\left(X_{n}: n=1,2, \ldots\right)$ be a sequence of independent and identically distributed positive random variables with continuous density function $f$. We define the sequence of successive records, $\left(K_{n}, n=0,1, \ldots\right)$, by $K_{0}:=0$ and, for $n \geqslant 0$,

  $$K_{n+1}:=\inf \left\{m>K_{n}: X_{m}>X_{K_{n}}\right\}$$

  The record process,$\left(R_{t}, t \geqslant 0\right)$, is then defined by

  $$R_{t}:=\#\left\{n \geqslant 1: X_{K_{n}} \leqslant t\right\}$$

  Explain why the increments of $R$ are independent. Show that $R_{t}$ is a Poisson random variable with parameter $-\log \{1-F(t)\}$ where $F(t)=\int_{0}^{t} f(s) d s$.

  [You may assume the following without proof: For fixed $t>0$, let $Y$ (respectively, $Z$ ) be the subsequence of $X$ obtained by retaining only those elements that are greater than (respectively, smaller than) $t$. Then $Y$ (respectively, $Z$ ) is a sequence of independent variables each having the distribution of $X_{1}$ conditioned on $X_{1}>t$ (respectively, $X_{1}<t$ ); and $Y$ and $Z$ are independent.]

  comment

• Paper 3, Section II, J

  Applied Probability | Part II, 2013

  Define the Moran model. Describe briefly the infinite sites model of mutations.

  We henceforth consider a population with $N$ individuals evolving according to the rules of the Moran model. In addition we assume:

  • the allelic type of any individual at any time lies in a given countable state space $S$;

  • individuals are subject to mutations at constant rate $u=\theta / N$, independently of the population dynamics;

  • each time a mutation occurs, if the allelic type of the individual was $x \in S$, it changes to $y \in S$ with probability $P(x, y)$, where $P(x, y)$ is a given Markovian transition matrix on $S$ that is symmetric:

  $$P(x, y)=P(y, x) \quad(x, y \in S)$$

  (i) Show that, if two individuals are sampled at random from the population at some time $t$, then the time to their most recent common ancestor has an exponential distribution, with a parameter that you should specify.

  (ii) Let $\Delta+1$ be the total number of mutations that accumulate on the two branches separating these individuals from their most recent common ancestor. Show that $\Delta+1$ is a geometric random variable, and specify its probability parameter $p$.

  (iii) The first individual is observed to be of type $x \in S$. Explain why the probability that the second individual is also of type $x$ is

  $$\mathbb{P}\left(X_{\Delta}=x \mid X_{0}=x\right),$$

  where $\left(X_{n}, n \geqslant 0\right)$ is a Markov chain on $S$ with transition matrix $P$ and is independent of $\Delta$.

  comment

• Paper 4, Section II, J

  Applied Probability | Part II, 2013

  (i) Define an $M / M / 1$ queue. Justifying briefly your answer, specify when this queue has a stationary distribution, and identify that distribution. State and prove Burke's theorem for this queue.

  (ii) Let $\left(L_{1}(t), \ldots, L_{N}(t), t \geqslant 0\right)$ denote a Jackson network of $N$ queues, where the entrance and service rates for queue $i$ are respectively $\lambda_{i}$ and $\mu_{i}$, and each customer leaving queue $i$ moves to queue $j$ with probability $p_{i j}$ after service. We assume $\sum_{j} p_{i j}<1$ for each $i=1, \ldots, N$; with probability $1-\sum_{j} p_{i j}$ a customer leaving queue $i$ departs from the system. State Jackson's theorem for this network. [You are not required to prove it.] Are the processes $\left(L_{1}(t), \ldots, L_{N}(t), t \geqslant 0\right)$ independent at equilibrium? Justify your answer.

  (iii) Let $D_{i}(t)$ be the process of final departures from queue $i$. Show that, at equilibrium, $\left(L_{1}(t), \ldots, L_{N}(t)\right)$ is independent of $\left(D_{i}(s), 1 \leqslant i \leqslant N, 0 \leqslant s \leqslant t\right)$. Show that, for each fixed $i=1, \ldots, N,\left(D_{i}(t), t \geqslant 0\right)$ is a Poisson process, and specify its rate.

  comment

Asymptotic Methods

• Paper 1, Section II, B

  Asymptotic Methods | Part II, 2013

  Suppose $\alpha>0$. Define what it means to say that

  $$F(x) \sim \frac{1}{\alpha x} \sum_{n=0}^{\infty} n !\left(\frac{-1}{\alpha x}\right)^{n}$$

  is an asymptotic expansion of $F(x)$ as $x \rightarrow \infty$. Show that $F(x)$ has no other asymptotic expansion in inverse powers of $x$ as $x \rightarrow \infty$.

  To estimate the value of $F(x)$ for large $x$, one may use an optimal truncation of the asymptotic expansion. Explain what is meant by this, and show that the error is an exponentially small quantity in $x$.

  Derive an integral respresentation for a function $F(x)$ with the above asymptotic expansion.

  comment

• Paper 3, Section II, B

  Asymptotic Methods | Part II, 2013

  Let

  $$I(x)=\int_{0}^{\pi} f(t) e^{i x \psi(t)} d t$$

  where $f(t)$ and $\psi(t)$ are smooth, and $\psi^{\prime}(t) \neq 0$ for $t>0 ;$ also $f(0) \neq 0$, $\psi(0)=a$, $\psi^{\prime}(0)=\psi^{\prime \prime}(0)=0$ and $\psi^{\prime \prime \prime}(0)=6 b>0$. Show that, as $x \rightarrow+\infty$,

  $$I(x) \sim f(0) e^{i(x a+\pi / 6)}\left(\frac{1}{27 b x}\right)^{1 / 3} \Gamma(1 / 3) .$$

  Consider the Bessel function

  $$J_{n}(x)=\frac{1}{\pi} \int_{0}^{\pi} \cos (n t-x \sin t) d t$$

  Show that, as $n \rightarrow+\infty$,

  $$J_{n}(n) \sim \frac{\Gamma(1 / 3)}{\pi} \frac{1}{(48)^{1 / 6}} \frac{1}{n^{1 / 3}}$$

  comment

• Paper 4, Section II, B

  Asymptotic Methods | Part II, 2013

  Show that the equation

  $$\frac{d^{2} y}{d x^{2}}+\frac{2}{x} \frac{d y}{d x}+\left(\frac{1}{x^{2}}-1\right) y=0$$

  has an irregular singular point at infinity. Using the Liouville-Green method, show that one solution has the asymptotic expansion

  $$y(x) \sim \frac{1}{x} e^{x}\left(1+\frac{1}{2 x}+\ldots\right)$$

  as $x \rightarrow \infty$

  comment

Classical Dynamics

• Paper 1, Section I, B

  Classical Dynamics | Part II, 2013

  Consider an $n$-dimensional dynamical system with generalized coordinates and momenta $\left(q_{i}, p_{i}\right), i=1,2, \ldots, n$.

  (a) Define the Poisson bracket $\{f, g\}$ of two functions $f\left(q_{i}, p_{i}, t\right)$ and $g\left(q_{i}, p_{i}, t\right)$.

  (b) Assuming Hamilton's equations of motion, prove that if a function $G\left(q_{i}, p_{i}\right)$ Poisson commutes with the Hamiltonian, that is $\{G, H\}=0$, then $G$ is a constant of the motion.

  (c) Assume that $q_{j}$ is an ignorable coordinate, that is the Hamiltonian does not depend on it explicitly. Using the formalism of Poisson brackets prove that the conjugate momentum $p_{j}$ is conserved.

  comment

• Paper 2, Section I, B

  Classical Dynamics | Part II, 2013

  (i) Consider a rigid body with principal moments of inertia $I_{1}, I_{2}, I_{3}$. Derive Euler's equations of torque-free motion,

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}, \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}, \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}, \end{aligned}$$

  with components of the angular velocity $\boldsymbol{\omega}=\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ given in the body frame.

  (ii) Use Euler's equations to show that the energy $E$ and the square of the total angular momentum $\mathbf{L}^{2}$ of the body are conserved.

  (iii) Consider a torque-free motion of a symmetric top with $I_{1}=I_{2}=\frac{1}{2} I_{3}$. Show that in the body frame the vector of angular velocity $\boldsymbol{\omega}$ precesses about the body-fixed $\mathbf{e}_{3}$ axis with constant angular frequency equal to $\omega_{3}$.

  comment

• Paper 2, Section II, B

  Classical Dynamics | Part II, 2013

  (i) The action for a system with a generalized coordinate $q$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

  (a) State the Principle of Least Action and derive the Euler-Lagrange equation.

  (b) Consider an arbitrary function $f(q, t)$. Show that $L^{\prime}=L+d f / d t$ leads to the same equation of motion.

  (ii) A wire frame $A B C$ in a shape of an equilateral triangle with side $a$ rotates in a horizontal plane with constant angular frequency $\omega$ about a vertical axis through $A$. A bead of mass $m$ is threaded on $B C$ and moves without friction. The bead is connected to $B$ and $C$ by two identical light springs of force constant $k$ and equilibrium length $a / 2$.

  (a) Introducing the displacement $\eta$ of the particle from the mid point of $B C$, determine the Lagrangian $L(\eta, \dot{\eta})$.

  (b) Derive the equation of motion. Identify the integral of the motion.

  (c) Describe the motion of the bead. Find the condition for there to be a stable equilibrium and find the frequency of small oscillations about it when it exists.

  comment

• Paper 3, Section I, B

  Classical Dynamics | Part II, 2013

  Two equal masses $m$ are connected to each other and to fixed points by three springs of force constant $5 k, k$ and $5 k$ as shown in the figure.

  

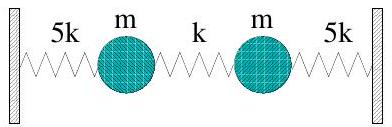
  (i) Write down the Lagrangian and derive the equations describing the motion of the system in the direction parallel to the springs.

  (ii) Find the normal modes and their frequencies. Comment on your results.

  comment

• Paper 4, Section I, B

  Classical Dynamics | Part II, 2013

  The Lagrangian for a heavy symmetric top of mass $M$, pinned at point $O$ which is a distance $l$ from the centre of mass, is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  (i) Starting with the fixed space frame $\left(\tilde{\mathbf{e}}_{\mathbf{1}}, \tilde{\mathbf{e}}_{2}, \tilde{\mathbf{e}}_{3}\right)$ and choosing $O$ at its origin, sketch the top with embedded body frame axis $\mathbf{e}_{3}$ being the symmetry axis. Clearly identify the Euler angles $(\theta, \phi, \psi)$.

  (ii) Obtain the momenta $p_{\theta}, p_{\phi}$ and $p_{\psi}$ and the Hamiltonian $H\left(\theta, \phi, \psi, p_{\theta}, p_{\phi}, p_{\psi}\right)$. Derive Hamilton's equations. Identify the three conserved quantities.

  comment

• Paper 4, Section II, B

  Classical Dynamics | Part II, 2013

  The motion of a particle of charge $q$ and mass $m$ in an electromagnetic field with scalar potential $\phi(\mathbf{r}, t)$ and vector potential $\mathbf{A}(\mathbf{r}, t)$ is characterized by the Lagrangian

  $$L=\frac{m \dot{\mathbf{r}}^{2}}{2}-q(\phi-\dot{\mathbf{r}} \cdot \mathbf{A})$$

  (i) Write down the Hamiltonian of the particle.

  (ii) Write down Hamilton's equations of motion for the particle.

  (iii) Show that Hamilton's equations are invariant under the gauge transformation

  $$\phi \rightarrow \phi-\frac{\partial \Lambda}{\partial t}, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda,$$

  for an arbitrary function $\Lambda(\mathbf{r}, t)$.

  (iv) The particle moves in the presence of a field such that $\phi=0$ and $\mathbf{A}=\left(-\frac{1}{2} y B, \frac{1}{2} x B, 0\right)$, where $(x, y, z)$ are Cartesian coordinates and $B$ is a constant.

  (a) Find a gauge transformation such that only one component of $\mathbf{A}(x, y, z)$ remains non-zero.

  (b) Determine the motion of the particle.

  (v) Now assume that $B$ varies very slowly with time on a time-scale much longer than $(q B / m)^{-1}$. Find the quantity which remains approximately constant throughout the motion.

  [You may use the expression for the action variable $I=\frac{1}{2 \pi} \oint p_{i} d q_{i}$.]

  comment

Coding and Cryptography

• Paper 1, Section I, H

  Coding and Cryptography | Part II, 2013

  A binary Huffman code is used for encoding symbols $1, \ldots, m$ occurring with respective probabilities $p_{1} \geqslant \cdots \geqslant p_{m}>0$ where $\sum_{1 \leqslant j \leqslant m} p_{j}=1$. Let $s_{1}$ be the length of a shortest codeword and $s_{m}$ the length of a longest codeword. Determine the maximal and minimal values of each of $s_{1}$ and $s_{m}$, and find binary trees for which they are attained.

  comment

• Paper 1, Section II, H

  Coding and Cryptography | Part II, 2013

  Define the bar product $C_{1} \mid C_{2}$ of binary linear codes $C_{1}$ and $C_{2}$, where $C_{2}$ is a subcode of $C_{1}$. Relate the rank and minimum distance of $C_{1} \mid C_{2}$ to those of $C_{1}$ and $C_{2}$ and justify your answer. Show that if $C^{\perp}$ denotes the dual code of $C$, then

  $$\left(C_{1} \mid C_{2}\right)^{\perp}=C_{2}^{\perp} \mid C_{1}^{\perp}$$

  Using the bar product construction, or otherwise, define the Reed-Muller code $\mathrm{RM}(d, r)$ for $0 \leqslant r \leqslant d$. Show that if $0 \leqslant r \leqslant d-1$, then the dual of $\mathrm{RM}(d, r)$ is again a Reed-Muller code.

  comment

• Paper 2, Section I, H

  Coding and Cryptography | Part II, 2013

  Let $A(n, d)$ denote the maximum size of a binary code of length $n$ with minimum distance $d$. For fixed $\delta$ with $0<\delta<1 / 2$, let $\alpha(\delta)=\limsup _{n} \frac{1}{n} \log _{2} A(n, n \delta)$. Show that

  $$1-H(\delta) \leqslant \alpha(\delta) \leqslant 1-H(\delta / 2)$$

  where $H(p)=-p \log _{2} p-(1-p) \log _{2}(1-p)$.

  [You may assume the GSV and Hamming bounds and any form of Stirling's theorem provided you state them clearly.]

  comment

• Paper 2, Section II, H

  Coding and Cryptography | Part II, 2013

  Define a BCH code of length $n$, where $n$ is odd, over the field of 2 elements with design distance $\delta$. Show that the minimum weight of such a code is at least $\delta$. [Results about the van der Monde determinant may be quoted without proof, provided they are stated clearly.]

  Consider a BCH code of length 31 over the field of 2 elements with design distance 8 . Show that the minimum distance is at least 11. [Hint: Let $\alpha$ be a primitive element in the field of $2^{5}$ elements, and consider the minimal polynomial for certain powers of $\left.\alpha .\right]$

  comment

• Paper 3, Section I, H

  Coding and Cryptography | Part II, 2013

  Describe briefly the Rabin cipher with modulus $N$, explaining how it can be deciphered by the intended recipient and why it is difficult for an eavesdropper to decipher it.

  The Cabinet decides to communicate using Rabin ciphers to maintain confidentiality. The Cabinet Secretary encrypts a message, represented as a positive integer $m$, using the Rabin cipher with modulus $N$ (with $0<m<N$ ) and publishes both the encrypted message and the modulus. The Defence Secretary deciphers this message to read it but then foolishly encrypts it again using a Rabin cipher with a different modulus $N^{\prime}$ (with $\left.m<N^{\prime}\right)$ and publishes the newly encrypted message and $N^{\prime}$. Mr Rime (the Leader of the Opposition) knows this has happened. Explain how Rime can work out what the original message was using the two different encrypted versions.

  Can Rime decipher other messages sent out by the Cabinet using the original modulus $N$ ?

  comment

• Paper 4, Section I, $4 \mathrm{H}$

  Coding and Cryptography | Part II, 2013

  Describe how a stream cipher works. What is a one-time pad?

  A one-time pad is used to send the message $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} y_{7}$ which is encoded as 0101011. In error, it is reused to send the message $y_{0} x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ which is encoded as 0100010 . Show that there are two possibilities for the substring $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$, and find them.

  comment

Cosmology

• Paper 1, Section I, D

  Cosmology | Part II, 2013

  The Friedmann equation and the fluid conservation equation for a closed isotropic and homogeneous cosmology are given by

  $$\begin{aligned} &\frac{\dot{a}^{2}}{a^{2}}=\frac{8 \pi G \rho}{3}-\frac{1}{a^{2}} \\ &\dot{\rho}+3 \frac{\dot{a}}{a}(\rho+P)=0 \end{aligned}$$

  where the speed of light is set equal to unity, $G$ is the gravitational constant, $a(t)$ is the expansion scale factor, $\rho$ is the fluid mass density and $P$ is the fluid pressure, and overdots denote differentiation with respect to the time coordinate $t$.

  If the universe contains only blackbody radiation and $a=0$ defines the zero of time $t$, show that

  $$a^{2}(t)=t\left(t_{*}-t\right)$$

  where $t_{*}$ is a constant. What is the physical significance of the time $t_{*}$ ? What is the value of the ratio $a(t) / t$ at the time when the scale factor is largest? Sketch the curve of $a(t)$ and identify its geometric shape.

  Briefly comment on whether this cosmological model is a good description of the observed universe at any time in its history.

  comment

• Paper 1, Section II, D

  Cosmology | Part II, 2013

  A spherically symmetric star of total mass $M_{s}$ has pressure $P(r)$ and mass density $\rho(r)$, where $r$ is the radial distance from its centre. These quantities are related by the equations of hydrostatic equilibrium and mass conservation:

  $$\begin{aligned} \frac{d P}{d r} &=-\frac{G M(r) \rho}{r^{2}} \\ \frac{d M}{d r} &=4 \pi \rho r^{2} \end{aligned}$$

  where $M(r)$ is the mass inside radius $r$.

  By integrating from the centre of the star at $r=0$, where $P=P_{c}$, to the surface of the star at $r=R_{s}$, where $P=P_{s}$, show that

  $$4 \pi R_{s}^{3} P_{s}=\Omega+3 \int_{0}^{M_{s}} \frac{P}{\rho} d M,$$

  where $\Omega$ is the total gravitational potential energy. Show that

  $$-\Omega>\frac{G M_{s}^{2}}{2 R_{s}}$$

  If the surface pressure is negligible and the star is a perfect gas of particles of mass $m$ with number density $n$ and $P=n k_{B} T$ at temperature $T$, and radiation pressure can be ignored, then show that

  $$3 \int_{0}^{M_{s}} \frac{P}{\rho} d M=\frac{3 k_{B}}{m} \bar{T},$$

  where $\bar{T}$ is the mean temperature of the star, which you should define.

  Hence, show that the mean temperature of the star satisfies the inequality

  $$\bar{T}>\frac{G M_{s} m}{6 k_{B} R_{s}}$$

  comment

• Paper 2, Section I, D

  Cosmology | Part II, 2013

  The linearised equation for the growth of small inhomogeneous density perturbations $\delta_{\mathbf{k}}$ with comoving wavevector $\mathbf{k}$ in an isotropic and homogeneous universe is

  $$\ddot{\delta}_{\mathbf{k}}+2 \frac{\dot{a}}{a} \dot{\delta}_{\mathbf{k}}+\left(\frac{c_{s}^{2} k^{2}}{a^{2}}-4 \pi G \rho\right) \delta_{\mathbf{k}}=0$$

  where $\rho$ is the matter density, $c_{s}=(d P / d \rho)^{1 / 2}$ is the sound speed, $P$ is the pressure, $a(t)$ is the expansion scale factor of the unperturbed universe, and overdots denote differentiation with respect to time $t$.

  Define the Jeans wavenumber and explain its physical meaning.

  Assume the unperturbed Friedmann universe has zero curvature and cosmological constant and it contains only zero-pressure matter, so that $a(t)=a_{0} t^{2 / 3}$. Show that the solution for the growth of density perturbations is given by

  $$\delta_{\mathbf{k}}=A(\mathbf{k}) t^{2 / 3}+B(\mathbf{k}) t^{-1}$$

  Comment briefly on the cosmological significance of this result.

  comment

• Paper 3, Section I, D

  Cosmology | Part II, 2013

  The number densities of protons of mass $m_{p}$ or neutrons of mass $m_{n}$ in kinetic equilibrium at temperature $T$, in the absence of any chemical potentials, are each given by (with $i=n$ or $p$ )

  $$n_{i}=g_{i}\left(\frac{m_{i} k_{B} T}{2 \pi \hbar^{2}}\right)^{3 / 2} \exp \left[-m_{i} c^{2} / k_{B} T\right]$$

  where $k_{B}$ is Boltzmann's constant and $g_{i}$ is the spin degeneracy.

  Use this to show, to a very good approximation, that the ratio of the number of neutrons to protons at a temperature $T \simeq 1 \mathrm{MeV} / k_{B}$ is given by

  $$\frac{n_{n}}{n_{p}}=\exp \left[-\left(m_{n}-m_{p}\right) c^{2} / k_{B} T\right]$$

  where $\left(m_{n}-m_{p}\right) c^{2}=1.3 \mathrm{MeV}$. Explain any approximations you have used.

  The reaction rate for weak interactions between protons and neutrons at energies $5 \mathrm{MeV} \geqslant k_{B} T \geqslant 0.8 \mathrm{MeV}$ is given by $\Gamma=\left(k_{B} T / 1 \mathrm{MeV}\right)^{5} \mathrm{~s}^{-1}$ and the expansion rate of the universe at these energies is given by $H=\left(k_{B} T / 1 M e V\right)^{2} s^{-1}$. Give an example of a weak interaction that can maintain equilibrium abundances of protons and neutrons at these energies. Show how the final abundance of neutrons relative to protons can be calculated and use it to estimate the mass fraction of the universe in helium- 4 after nucleosynthesis.

  What would have happened to the helium abundance if the proton and neutron masses had been exactly equal?

  comment

• Paper 3, Section II, D

  Cosmology | Part II, 2013

  The contents of a spatially homogeneous and isotropic universe are modelled as a finite mass $M$ of pressureless material whose radius $r(t)$ evolves from some constant reference radius $r_{0}$ in proportion to the time-dependent scale factor $a(t)$, with

  $$r(t)=a(t) r_{0}$$

  (i) Show that this motion leads to expansion governed by Hubble's Law. If this universe is expanding, explain why there will be a shift in the frequency of radiation between its emission from a distant object and subsequent reception by an observer. Define the redshift $z$ of the observed object in terms of the values of the scale factor $a(t)$ at the times of emission and reception.

  (ii) The expanding universal mass $M$ is given a small rotational perturbation, with angular velocity $\omega$, and its angular momentum is subsequently conserved. If deviations from spherical expansion can be neglected, show that its linear rotational velocity will fall as $V \propto a^{-n}$, where you should determine the value of $n$. Show that this perturbation will become increasingly insignificant compared to the expansion velocity as the universe expands if $a \propto t^{2 / 3}$.

  (iii) A distant cloud of intermingled hydrogen (H) atoms and carbon monoxide (CO) molecules has its redshift determined simultaneously in two ways: by detecting $21 \mathrm{~cm}$ radiation from atomic hydrogen and by detecting radiation from rotational transitions in CO molecules. The ratio of the $21 \mathrm{~cm}$ atomic transition frequency to the CO rotational transition frequency is proportional to $\alpha^{2}$, where $\alpha$ is the fine structure constant. It is suggested that there may be a small difference in the value of the constant $\alpha$ between the times of emission and reception of the radiation from the cloud.

  Show that the difference in the redshift values for the cloud, $\Delta z=z_{C O}-z_{21}$, determined separately by observations of the $\mathrm{H}$ and $\mathrm{CO}$ transitions, is related to $\delta \alpha=$ $\alpha_{r}-\alpha_{e}$, the difference in $\alpha$ values at the times of reception and emission, by

  $$\Delta z=2\left(\frac{\delta \alpha}{\alpha_{r}}\right)\left(1+z_{C O}\right)$$

  (iv) The universe today contains $30 \%$ of its total density in the form of pressureless matter and $70 \%$ in the form of a dark energy with constant redshift-independent density. If these are the only two significant constituents of the universe, show that their densities were equal when the scale factor of the universe was approximately equal to $75 \%$ of its present value.

  comment

• Paper 4, Section I, D

  Cosmology | Part II, 2013

  List the relativistic species of bosons and fermions from the standard model of particle physics that are present in the early universe when the temperature falls to $1 \mathrm{MeV} / \mathrm{k}_{B}$.

  Which of the particles above will be interacting when the temperature is above $1 \mathrm{MeV} / k_{B}$ and between $1 \mathrm{MeV} / k_{B} \geq T \geq 0.51 \mathrm{MeV} / k_{B}$, respectively?

  Explain what happens to the populations of particles present when the temperature falls to $0.51 \mathrm{MeV} / k_{B}$.

  The entropy density of fermion and boson species with temperature $T$ is $s \propto g_{s} T^{3}$, where $g_{s}$ is the number of relativistic spin degrees of freedom, that is,

  $$g_{s}=\sum_{\text {bosons }} g_{i}+\frac{7}{8} \sum_{\text {fermions }} g_{i}$$

  Show that when the temperature of the universe falls below $0.51 \mathrm{MeV} / k_{B}$ the ratio of the neutrino and photon temperatures will be given by

  $$\frac{T_{\nu}}{T_{\gamma}}=\left(\frac{4}{11}\right)^{1 / 3}$$

  comment

Differential Geometry

• Paper 1, Section II, H

  Differential Geometry | Part II, 2013

  For $f: X \rightarrow Y$ a smooth map of manifolds, define the concepts of critical point, critical value and regular value.

  With the obvious identification of $\mathbf{C}$ with $\mathbf{R}^{2}$, and hence also of $\mathbf{C}^{3}$ with $\mathbf{R}^{6}$, show that the complex-valued polynomial $z_{1}^{3}+z_{2}^{2}+z_{3}^{2}$ determines a smooth map $f: \mathbf{R}^{6} \rightarrow \mathbf{R}^{2}$ whose only critical point is at the origin. Hence deduce that $V:=f^{-1}((0,0)) \backslash\{\mathbf{0}\} \subset \mathbf{R}^{6}$ is a 4-dimensional manifold, and find the equations of its tangent space at any given point $\left(z_{1}, z_{2}, z_{3}\right) \in V$.

  Now let $S^{5} \subset \mathbf{C}^{3}=\mathbf{R}^{6}$ be the unit 5 -sphere, defined by $\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}+\left|z_{3}\right|^{2}=1$. Given a point $P=\left(z_{1}, z_{2}, z_{3}\right) \in S^{5} \cap V$, by considering the vector $\left(2 z_{1}, 3 z_{2}, 3 z_{3}\right) \in \mathbf{C}^{3}=\mathbf{R}^{6}$ or otherwise, show that not all tangent vectors to $V$ at $P$ are tangent to $S^{5}$. Deduce that $S^{5} \cap V \subset \mathbf{R}^{6}$ is a compact three-dimensional manifold.

  [Standard results may be quoted without proof if stated carefully.]

  comment

• Paper 2, Section II, H

  Differential Geometry | Part II, 2013

  Let $\alpha:[0, L] \rightarrow \mathbf{R}^{3}$ be a regular curve parametrized by arc length having nowherevanishing curvature. State the Frenet relations between the tangent, normal and binormal vectors at a point, and their derivatives.

  Let $S \subset \mathbf{R}^{3}$ be a smooth oriented surface. Define the Gauss map $N: S \rightarrow S^{2}$, and show that its derivative at $P \in S, d N_{P}: T_{P} S \rightarrow T_{P} S$, is self-adjoint. Define the Gaussian curvature of $S$ at $P$.

  Now suppose that $\alpha:[0, L] \rightarrow \mathbf{R}^{3}$ has image in $S$ and that its normal curvature is zero for all $s \in[0, L]$. Show that the Gaussian curvature of $S$ at a point $P=\alpha(s)$ of the curve is $K(P)=-\tau(s)^{2}$, where $\tau(s)$ denotes the torsion of the curve.

  If $S \subset \mathbf{R}^{3}$ is a standard embedded torus, show that there is a curve on $S$ for which the normal curvature vanishes and the Gaussian curvature of $S$ is zero at all points of the curve.

  comment

• Paper 3, Section II, H

  Differential Geometry | Part II, 2013

  We say that a parametrization $\phi: U \rightarrow S \subset \mathbf{R}^{3}$ of a smooth surface $S$ is isothermal if the coefficients of the first fundamental form satisfy $F=0$ and $E=G=\lambda(u, v)^{2}$, for some smooth non-vanishing function $\lambda$ on $U$. For an isothermal parametrization, prove that

  $$\phi_{u u}+\phi_{v v}=2 \lambda^{2} H \mathbf{N}$$

  where $\mathbf{N}$ denotes the unit normal vector and $H$ the mean curvature, which you may assume is given by the formula

  $$H=\frac{g+e}{2 \lambda^{2}}$$

  where $g=-\left\langle\mathbf{N}_{u}, \phi_{u}\right\rangle$ and $e=-\left\langle\mathbf{N}_{v}, \phi_{v}\right\rangle$ are coefficients in the second fundamental form.

  Given a parametrization $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$ of a surface $S \subset \mathbf{R}^{3}$, we consider the complex valued functions on $U$ :

  $$\theta_{1}=x_{u}-i x_{v}, \quad \theta_{2}=y_{u}-i y_{v}, \quad \theta_{3}=z_{u}-i z_{v}$$

  Show that $\phi$ is isothermal if and only if $\theta_{1}^{2}+\theta_{2}^{2}+\theta_{3}^{2}=0$. If $\phi$ is isothermal, show that $S$ is a minimal surface if and only if $\theta_{1}, \theta_{2}, \theta_{3}$ are holomorphic functions of the complex variable $\zeta=u+i v$

  Consider the holomorphic functions on $D:=\mathbf{C} \backslash \mathbf{R}_{\geqslant 0}$ (with complex coordinate $\zeta=u+i v$ on $\mathbf{C})$ given by

  $$\theta_{1}:=\frac{1}{2}\left(1-\zeta^{-2}\right), \quad \theta_{2}:=-\frac{i}{2}\left(1+\zeta^{-2}\right), \quad \theta_{3}:=-\zeta^{-1}$$

  Find a smooth map $\phi(u, v)=(x(u, v), y(u, v), z(u, v)): D \rightarrow \mathbf{R}^{3}$ for which $\phi(-1,0)=\mathbf{0}$ and the $\theta_{i}$ defined by (2) satisfy the equations (1). Show furthermore that $\phi$ extends to a smooth map $\tilde{\phi}: \mathbf{C}^{*} \rightarrow \mathbf{R}^{3}$. If $w=x+i y$ is the complex coordinate on $\mathbf{C}$, show that

  $$\widetilde{\phi}(\exp (i w))=(\cosh y \cos x+1, \cosh y \sin x, y)$$

  comment

• Paper 4, Section II, H

  Differential Geometry | Part II, 2013

  Define what is meant by the geodesic curvature $k_{g}$ of a regular curve $\alpha: I \rightarrow S$ parametrized by arc length on a smooth oriented surface $S \subset \mathbf{R}^{3}$. If $S$ is the unit sphere in $\mathbf{R}^{3}$ and $\alpha: I \rightarrow S$ is a parametrized geodesic circle of radius $\phi$, with $0<\phi<\pi / 2$, justify the fact that $\left|k_{g}\right|=\cot \phi$.

  State the general form of the Gauss-Bonnet theorem with boundary on an oriented surface $S$, explaining briefly the terms which occur.

  Let $S \subset \mathbf{R}^{3}$ now denote the circular cone given by $z>0$ and $x^{2}+y^{2}=z^{2} \tan ^{2} \phi$, for a fixed choice of $\phi$ with $0<\phi<\pi / 2$, and with a fixed choice of orientation. Let $\alpha: I \rightarrow S$ be a simple closed piecewise regular curve on $S$, with (signed) exterior angles $\theta_{1}, \ldots, \theta_{N}$ at the vertices (that is, $\theta_{i}$ is the angle between limits of tangent directions, with sign determined by the orientation). Suppose furthermore that the smooth segments of $\alpha$ are geodesic curves. What possible values can $\theta_{1}+\cdots+\theta_{N}$ take? Justify your answer.

  [You may assume that a simple closed curve in $\mathbf{R}^{2}$ bounds a region which is homeomorphic to a disc. Given another simple closed curve in the interior of this region, you may assume that the two curves bound a region which is homeomorphic to an annulus.]

  comment

Dynamical Systems

• Paper 1, Section I, C

  Dynamical Systems | Part II, 2013

  Consider the dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{n}$ which has a hyperbolic fixed point at the origin.

  Define the stable and unstable invariant subspaces of the system linearised about the origin. Give a constraint on the dimensions of these two subspaces.

  Define the local stable and unstable manifolds of the origin for the system. How are these related to the invariant subspaces of the linearised system?

  For the system

  $$\begin{aligned} &\dot{x}=-x+x^{2}+y^{2} \\ &\dot{y}=y+y^{2}-x^{2} \end{aligned}$$

  calculate the stable and unstable manifolds of the origin, each correct up to and including cubic order.

  comment

• Paper 2, Section I, $7 \mathrm{C}$

  Dynamical Systems | Part II, 2013

  Let $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ be a two-dimensional dynamical system with a fixed point at $\mathbf{x}=\mathbf{0}$. Define a Lyapunov function $V(\mathbf{x})$ and explain what it means for $\mathbf{x}=\mathbf{0}$ to be Lyapunov stable.

  For the system

  $$\begin{aligned} &\dot{x}=-x-2 y+x^{3} \\ &\dot{y}=-y+x+\frac{1}{2} y^{3}+x^{2} y \end{aligned}$$

  determine the values of $C$ for which $V=x^{2}+C y^{2}$ is a Lyapunov function in a sufficiently small neighbourhood of the origin.

  For the case $C=2$, find $V_{1}$ and $V_{2}$ such that $V(\mathbf{x})<V_{1}$ at $t=0$ implies that $V \rightarrow 0$ as $t \rightarrow \infty$ and $V(\mathbf{x})>V_{2}$ at $t=0$ implies that $V \rightarrow \infty$ as $t \rightarrow \infty$

  comment

• Paper 3, Section I, C

  Dynamical Systems | Part II, 2013

  A one-dimensional map is defined by

  $$x_{n+1}=F\left(x_{n}, \mu\right)$$

  where $\mu$ is a parameter. What is the condition for a bifurcation of a fixed point $x_{*}$ of $F$ ?

  Let $F(x, \mu)=x\left(x^{2}-2 x+\mu\right)$. Find the fixed points and show that bifurcations occur when $\mu=-1, \mu=1$ and $\mu=2$. Sketch the bifurcation diagram, showing the locus and stability of the fixed points in the $(x, \mu)$ plane and indicating the type of each bifurcation.

  comment

• Paper 3, Section II, C

  Dynamical Systems | Part II, 2013

  Let $f: I \rightarrow I$ be a continuous map of an interval $I \subset \mathbb{R}$. Explain what is meant by the statements (a) $f$ has a horseshoe and (b) $f$ is chaotic according to Glendinning's definition of chaos.

  Assume that $f$ has a 3-cycle $\left\{x_{0}, x_{1}, x_{2}\right\}$ with $x_{1}=f\left(x_{0}\right), x_{2}=f\left(x_{1}\right), x_{0}=f\left(x_{2}\right)$, $x_{0}<x_{1}<x_{2}$. Prove that $f^{2}$ has a horseshoe. [You may assume the Intermediate Value Theorem.]

  Represent the effect of $f$ on the intervals $I_{a}=\left[x_{0}, x_{1}\right]$ and $I_{b}=\left[x_{1}, x_{2}\right]$ by means of a directed graph. Explain how the existence of the 3 -cycle corresponds to this graph.

  The map $g: I \rightarrow I$ has a 4-cycle $\left\{x_{0}, x_{1}, x_{2}, x_{3}\right\}$ with $x_{1}=g\left(x_{0}\right), x_{2}=g\left(x_{1}\right)$, $x_{3}=g\left(x_{2}\right)$ and $x_{0}=g\left(x_{3}\right)$. If $x_{0}<x_{3}<x_{2}<x_{1}$ is $g$ necessarily chaotic? [You may use a suitable directed graph as part of your argument.]

  How does your answer change if $x_{0}<x_{2}<x_{1}<x_{3}$ ?

  comment

• Paper 4, Section I, C

  Dynamical Systems | Part II, 2013

  Consider the system

  $$\begin{aligned} &\dot{x}=y+a x+b x^{3} \\ &\dot{y}=-x \end{aligned}$$

  What is the Poincaré index of the single fixed point? If there is a closed orbit, why must it enclose the origin?

  By writing $\dot{x}=\partial H / \partial y+g(x)$ and $\dot{y}=-\partial H / \partial x$ for suitable functions $H(x, y)$ and $g(x)$, show that if there is a closed orbit $\mathcal{C}$ then

  $$\oint_{\mathcal{C}}\left(a x+b x^{3}\right) x d t=0$$

  Deduce that there is no closed orbit when $a b>0$.

  If $a b<0$ and $a$ and $b$ are both $O(\epsilon)$, where $\epsilon$ is a small parameter, then there is a single closed orbit that is to within $O(\epsilon)$ a circle of radius $R$ centred on the origin. Deduce a relation between $a, b$ and $R$.

  comment

• Paper 4, Section II, C

  Dynamical Systems | Part II, 2013

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=(x+y+a)(x-y+a) \\ &\dot{y}=y-x^{2}-b \end{aligned}$$

  where $a>0$.

  Find the fixed points of the dynamical system. Show that for any fixed value of $a$ there exist three values $b_{1}>b_{2} \geqslant b_{3}$ of $b$ where a bifurcation occurs. Show that $b_{2}=b_{3}$ when $a=1 / 2$.

  In the remainder of this question set $a=1 / 2$.

  (i) Being careful to explain your reasoning, show that the extended centre manifold for the bifurcation at $b=b_{1}$ can be written in the form $X=\alpha Y+\beta \mu+p(Y, \mu)$, where $X$ and $Y$ denote the departures from the values of $x$ and $y$ at the fixed point, $b=b_{1}+\mu, \alpha$ and $\beta$ are suitable constants (to be determined) and $p$ is quadratic to leading order. Derive a suitable approximate form for $p$, and deduce the nature of the bifurcation and the stability of the different branches of the steady state solution near the bifurcation.

  (ii) Repeat the calculations of part (i) for the bifurcation at $b=b_{2}$.

  (iii) Sketch the $x$ values of the fixed points as functions of $b$, indicating the nature of the bifurcations and where each branch is stable.

  comment

Electrodynamics

• Paper 1, Section II, 36B

  Electrodynamics | Part II, 2013

  (i) Starting from

  $$F^{\mu \nu}=\left(\begin{array}{cccc} 0 & E_{1} / c & E_{2} / c & E_{3} / c \\ -E_{1} / c & 0 & B_{3} & -B_{2} \\ -E_{2} / c & -B_{3} & 0 & B_{1} \\ -E_{3} / c & B_{2} & -B_{1} & 0 \end{array}\right)$$

  and performing a Lorentz transformation with $\gamma=1 / \sqrt{1-u^{2} / c^{2}}$, using

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma u / c & 0 & 0 \\ -\gamma u / c & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  show how $\mathbf{E}$ and $\mathbf{B}$ transform under a Lorentz transformation.

  (ii) By taking the limit $c \rightarrow \infty$, obtain the behaviour of $\mathbf{E}$ and $\mathbf{B}$ under a Galilei transfomation and verify the invariance under Galilei transformations of the nonrelativistic equation

  $$m \frac{d \mathbf{v}}{d t}=q(\mathbf{E}+\mathbf{v} \times \mathbf{B})$$

  (iii) Show that Maxwell's equations admit solutions of the form

  $$\mathbf{E}=\mathbf{E}_{0} f(t-\mathbf{n} \cdot \mathbf{x} / c), \quad \mathbf{B}=\mathbf{B}_{0} f(t-\mathbf{n} \cdot \mathbf{x} / c)$$

  where $f$ is an arbitrary function, $\mathbf{n}$ is a unit vector, and the constant vectors $\mathbf{E}_{0}$ and $\mathbf{B}_{0}$ are subject to restrictions which should be stated.

  (iv) Perform a Galilei transformation of a solution $(\star)$, with $\mathbf{n}=(1,0,0)$. Show that, by a particular choice of $u$, the solution may brought to the form

  $$\tilde{\mathbf{E}}=\tilde{\mathbf{E}}_{0} g(\tilde{x}), \quad \tilde{\mathbf{B}}=\tilde{\mathbf{B}}_{0} g(\tilde{x}),$$

  where $g$ is an arbitrary function and $\tilde{x}$ is a spatial coordinate in the rest frame. By showing that $(t)$ is not a solution of Maxwell's equations in the boosted frame, conclude that Maxwell's equations are not invariant under Galilei transformations.

  comment

• Paper 3, Section II, 36B

  Electrodynamics | Part II, 2013

  (i) Obtain Maxwell's equations in empty space from the action functional

  $$S\left[A_{\mu}\right]=-\frac{1}{\mu_{0}} \int d^{4} x \frac{1}{4} F_{\mu \nu} F^{\mu \nu}$$

  where $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$.

  (ii) A modification of Maxwell's equations has the action functional

  $$\tilde{S}\left[A_{\mu}\right]=-\frac{1}{\mu_{0}} \int d^{4} x\left\{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+\frac{1}{2 \lambda^{2}} A_{\mu} A^{\mu}\right\},$$

  where again $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ and $\lambda$ is a constant. Obtain the equations of motion of this theory and show that they imply $\partial_{\mu} A^{\mu}=0$.

  (iii) Show that the equations of motion derived from $\tilde{S}$ admit solutions of the form

  $$A^{\mu}=A_{0}^{\mu} e^{i k_{\nu} x^{\nu}}$$

  where $A_{0}^{\mu}$ is a constant 4-vector, and the 4 -vector $k_{\mu}$ satisfies $A_{0}^{\mu} k_{\mu}=0$ and $k_{\mu} k^{\mu}=-1 / \lambda^{2}$.

  (iv) Show further that the tensor

  $$T_{\mu \nu}=\frac{1}{\mu_{0}}\left\{F_{\mu \sigma} F_{\nu}^{\sigma}-\frac{1}{4} \eta_{\mu \nu} F_{\alpha \beta} F^{\alpha \beta}-\frac{1}{2 \lambda^{2}}\left(\eta_{\mu \nu} A_{\alpha} A^{\alpha}-2 A_{\mu} A_{\nu}\right)\right\}$$

  is conserved, that is $\partial^{\mu} T_{\mu \nu}=0$.

  comment

• Paper 4, Section II, 35B

  Electrodynamics | Part II, 2013

  (i) For a time-dependent source, confined within a domain $D$, show that the time derivative $\dot{d}$ of the dipole moment $\mathbf{d}$ satisfies

  $$\dot{\mathbf{d}}=\int_{D} d^{3} y \mathbf{J}(\mathbf{y})$$

  where $\mathbf{J}$ is the current density.

  (ii) The vector potential $\mathbf{A}(\mathbf{x}, t)$ due to a time-dependent source is given by

  $$\mathbf{A}=\frac{1}{r} f(t-r / c) \mathbf{k}$$

  where $r=|\mathbf{x}| \neq 0$, and $\mathbf{k}$ is the unit vector in the $z$ direction. Calculate the resulting magnetic field $\mathbf{B}(\mathbf{x}, t)$. By considering the magnetic field for small $r$ show that the dipole moment of the effective source satisfies

  $$\frac{\mu_{0}}{4 \pi} \dot{\mathbf{d}}=f(t) \mathbf{k}$$

  Calculate the asymptotic form of the magnetic field $\mathbf{B}$ at very large $r$.

  (iii) Using the equation

  $$\frac{\partial \mathbf{E}}{\partial t}=c^{2} \nabla \times \mathbf{B}$$

  calculate $\mathbf{E}$ at very large $r$. Show that $\mathbf{E}, \mathbf{B}$ and $\hat{\mathbf{r}}=\mathbf{x} /|\mathbf{x}|$ form a right-handed triad, and moreover $|\mathbf{E}|=c|\mathbf{B}|$. How do $|\mathbf{E}|$ and $|\mathbf{B}|$ depend on $r ?$ What is the significance of this?

  (iv) Calculate the power $P(\theta, \phi)$ emitted per unit solid angle and sketch its dependence on $\theta$. Show that the emitted radiation is polarised and describe how the plane of polarisation (that is, the plane in which $\mathbf{E}$ and $\hat{\mathbf{r}}$ lie) depends on the direction of the dipole. Suppose the dipole moment has constant amplitude and constant frequency and so the radiation is monochromatic with wavelength $\lambda$. How does the emitted power depend on $\lambda$ ?

  comment

Fluid Dynamics II

• Paper 1, Section II, A

  Fluid Dynamics II | Part II, 2013

  The velocity field $\mathbf{u}$ and stress tensor $\sigma$ satisfy the Stokes equations in a volume $V$ bounded by a surface $S$. Let $\hat{\mathbf{u}}$ be another solenoidal velocity field. Show that

  $$\int_{S} \sigma_{i j} n_{j} \hat{u}_{i} d S=\int_{V} 2 \mu e_{i j} \hat{e}_{i j} d V$$

  where $\mathbf{e}$ and $\hat{\mathbf{e}}$ are the strain-rates corresponding to the velocity fields $\mathbf{u}$ and $\hat{\mathbf{u}}$ respectively, and $\mathbf{n}$ is the unit normal vector out of $V$. Hence, or otherwise, prove the minimum dissipation theorem for Stokes flow.

  A particle moves at velocity $\mathbf{U}$ through a highly viscous fluid of viscosity $\mu$ contained in a stationary vessel. As the particle moves, the fluid exerts a drag force $\mathbf{F}$ on it. Show that

  $$-\mathbf{F} \cdot \mathbf{U}=\int_{V} 2 \mu e_{i j} e_{i j} d V .$$

  Consider now the case when the particle is a small cube, with sides of length $\ell$, moving in a very large vessel. You may assume that

  $$\mathbf{F}=-k \mu \ell \mathbf{U}$$

  for some constant $k$. Use the minimum dissipation theorem, being careful to declare the domain(s) involved, to show that

  $$3 \pi \leqslant k \leqslant 3 \sqrt{3} \pi .$$

  [You may assume Stokes' result for the drag on a sphere of radius $a, \mathbf{F}=-6 \pi \mu a \mathbf{U}$.]

  comment

• Paper 2, Section II, A

  Fluid Dynamics II | Part II, 2013

  Write down the boundary-layer equations for steady two-dimensional flow of a viscous incompressible fluid with velocity $U(x)$ outside the boundary layer. Find the boundary layer thickness $\delta(x)$ when $U(x)=U_{0}$, a constant. Show that the boundarylayer equations can be satisfied in this case by a streamfunction $\psi(x, y)=g(x) f(\eta)$ with suitable scaling function $g(x)$ and similarity variable $\eta$. Find the equation satisfied by $f$ and the associated boundary conditions.

  Find the drag on a thin two-dimensional flat plate of finite length $L$ placed parallel to a uniform flow. Why does the drag not increase in proportion to the length of the plate? [You may assume that the boundary-layer solution is applicable except in negligibly small regions near the leading and trailing edges. You may also assume that $f^{\prime \prime}(0)=0.33$.]

  comment

• Paper 3, Section II, A

  Fluid Dynamics II | Part II, 2013

  A disk hovers on a cushion of air above an air-table - a fine porous plate through which a constant flux of air is pumped. Let the disk have a radius $R$ and a weight $M g$ and hover at a low height $h \ll R$ above the air-table. Let the volume flux of air, which has density $\rho$ and viscosity $\mu$, be $w$ per unit surface area. The conditions are such that $\rho w h^{2} / \mu R \ll 1$. Explain the significance of this restriction.

  Find the pressure distribution in the air under the disk. Show that this pressure balances the weight of the disk if

  $$h=R\left(\frac{3 \pi \mu R w}{2 M g}\right)^{1 / 3}$$

  comment

• Paper 4, Section II, A

  Fluid Dynamics II | Part II, 2013

  Consider the flow of an incompressible fluid of uniform density $\rho$ and dynamic viscosity $\mu$. Show that the rate of viscous dissipation per unit volume is given by

  $$\Phi=2 \mu e_{i j} e_{i j}$$

  where $e_{i j}$ is the strain rate.

  Determine expressions for $e_{i j}$ and $\Phi$ when the flow is irrotational with velocity potential $\phi$.

  In deep water a linearised wave with a surface displacement $\eta=a \cos (k x-\omega t)$ has a velocity potential $\phi=-(\omega a / k) e^{-k z} \sin (k x-\omega t)$. Hence determine the rate of the viscous dissipation, averaged over a wave period $2 \pi / \omega$, for an irrotational surface wave of wavenumber $k$ and small amplitude $a \ll 1 / k$ in a fluid with very small viscosity $\mu \ll \rho \omega / k^{2}$ and great depth $H \gg 1 / k$.

  Calculate the depth-integrated kinetic energy per unit wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order as $e^{-\gamma t}$, where $\gamma$ should be found.

  comment

Further Complex Methods

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2013

  Prove that there are no second order linear ordinary homogeneous differential equations for which all points in the extended complex plane are analytic.

  Find all such equations which have one regular singular point at $z=0$.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2013

  Show that the equation

  $$(z-1) w^{\prime \prime}-z w^{\prime}+(4-2 z) w=0$$

  has solutions of the form $w(z)=\int_{\gamma} \exp (z t) f(t) d t$, where

  $$f(t)=\frac{\exp (-t)}{(t-a)(t-b)^{2}}$$

  and the contour $\gamma$ is any closed curve in the complex plane, where $a$ and $b$ are real constants which should be determined.

  Use this to find the general solution, evaluating the integrals explicitly.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2013

  (i) Find all branch points of $\left(z^{3}-1\right)^{1 / 4}$ on an extended complex plane.

  (ii) Use a branch cut to evaluate the integral

  $$\int_{-2}^{2}\left(4-x^{2}\right)^{1 / 2} d x$$

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2013

  The Beta function is defined for $\operatorname{Re}(z)>0$ as

  $$B(z, q)=\int_{0}^{1} t^{q-1}(1-t)^{z-1} d t, \quad(\operatorname{Re}(q)>0)$$

  and by analytic continuation elsewhere in the complex $z$-plane.

  Show that:

  (i) $(z+q) B(z+1, q)=z B(z, q)$;

  (ii) $\Gamma(z)^{2}=B(z, z) \Gamma(2 z)$.

  By considering $\Gamma\left(z / 2^{m}\right)$ for all positive integers $m$, deduce that $\Gamma(z) \neq 0$ for all $z$ with $\operatorname{Re}(z)>0$.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2013

  Let a real-valued function $u=u(x, y)$ be the real part of a complex-valued function $f=f(z)$ which is analytic in the neighbourhood of a point $z=0$, where $z=x+i y .$ Derive a formula for $f$ in terms of $u$ and use it to find an analytic function $f$ whose real part is

  $$\frac{x^{3}+x^{2}-y^{2}+x y^{2}}{(x+1)^{2}+y^{2}}$$

  and such that $f(0)=0$.

  comment

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2013

  Let the function $f(z)$ be analytic in the upper half-plane and such that $|f(z)| \rightarrow 0$ as $|z| \rightarrow \infty$. Show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x} d x=i \pi f(0),$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  Use the Cauchy integral theorem to show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{u(x, 0)}{x-t} d x=-\pi v(t, 0), \quad \mathcal{P} \int_{-\infty}^{\infty} \frac{v(x, 0)}{x-t} d x=\pi u(t, 0),$$

  where $u(x, y)$ and $v(x, y)$ are the real and imaginary parts of $f(z)$.

  comment

Galois Theory

• Paper 1, Section II, I

  Galois Theory | Part II, 2013

  (i) Give an example of a field $F$, contained in $\mathbb{C}$, such that $X^{4}+1$ is a product of two irreducible quadratic polynomials in $F[X]$. Justify your answer.

  (ii) Let $F$ be any extension of degree 3 over $\mathbb{Q}$. Prove that the polynomial $X^{4}+1$ is irreducible over $F$.

  (iii) Give an example of a prime number $p$ such that $X^{4}+1$ is a product of two irreducible quadratic polynomials in $\mathbb{F}_{p}[X]$. Justify your answer.

  [Standard facts on fields, extensions, and finite fields may be quoted without proof, as long as they are stated clearly.]

  comment

• Paper 2, Section II, I

  Galois Theory | Part II, 2013

  For a positive integer $N$, let $\mathbb{Q}\left(\boldsymbol{\mu}_{N}\right)$ be the cyclotomic field obtained by adjoining all $N$-th roots of unity to $\mathbb{Q}$. Let $F=\mathbb{Q}\left(\boldsymbol{\mu}_{24}\right)$.

  (i) Determine the Galois group of $F$ over $\mathbb{Q}$.

  (ii) Find all $N>1$ such that $\mathbb{Q}\left(\boldsymbol{\mu}_{N}\right)$ is contained in $F$.

  (iii) List all quadratic and quartic extensions of $\mathbb{Q}$ which are contained in $F$, in the form $\mathbb{Q}(\alpha)$ or $\mathbb{Q}(\alpha, \beta)$. Indicate which of these fields occurred in (ii).

  [Standard facts on the Galois groups of cyclotomic fields and the fundamental theorem of Galois theory may be used freely without proof.]

  comment

• Paper 3, Section II, I

  Galois Theory | Part II, 2013

  Let $p$ be a prime number and $F$ a field of characteristic $p$. Let $\operatorname{Fr}_{p}: F \rightarrow F$ be the Frobenius map defined by $\operatorname{Fr}_{p}(x)=x^{p}$ for all $x \in F$.

  (i) Prove that $\operatorname{Fr}_{p}$ is a field automorphism when $F$ is a finite field.

  (ii) Is the same true for an arbitrary algebraic extension $F$ of $\mathbb{F}_{p}$ ? Justify your answer.

  (iii) Let $F=\mathbb{F}_{p}\left(X_{1}, \ldots, X_{n}\right)$ be the rational function field in $n$ variables where $n \geqslant 1$ over $\mathbb{F}_{p}$. Determine the image of $\operatorname{Fr}_{p}: F \rightarrow F$, and show that $\operatorname{Fr}_{p}$ makes $F$ into an extension of degree $p^{n}$ over a subfield isomorphic to $F$. Is it a separable extension?

  comment

• Paper 4, Section II, I

  Galois Theory | Part II, 2013

  (i) Let $\zeta_{N}=\mathrm{e}^{2 \pi i / N} \in \mathbb{C}$ for $N \geqslant 1$. For the cases $N=11,13$, is it possible to express $\zeta_{N}$, starting with integers and using rational functions and (possibly nested) radicals? If it is possible, briefly explain how this is done, assuming standard facts in Galois Theory.

  (ii) Let $F=\mathbb{C}(X, Y, Z)$ be the rational function field in three variables over $\mathbb{C}$, and for integers $a, b, c \geqslant 1$ let $K=\mathbb{C}\left(X^{a}, Y^{b}, Z^{c}\right)$ be the subfield of $F$ consisting of all rational functions in $X^{a}, Y^{b}, Z^{c}$ with coefficients in $\mathbb{C}$. Show that $F / K$ is Galois, and determine its Galois group. [Hint: For $\alpha, \beta, \gamma \in \mathbb{C}^{\times}$, the map $(X, Y, Z) \longmapsto(\alpha X, \beta Y, \gamma Z)$ is an automorphism of $F$.]

  comment

General Relativity

• Paper 1, Section II, 37D

  General Relativity | Part II, 2013

  The curve $\gamma, x^{a}=x^{a}(\lambda)$, is a geodesic with affine parameter $\lambda$. Write down the geodesic equation satisfied by $x^{a}(\lambda)$.

  Suppose the parameter is changed to $\mu(\lambda)$, where $d \mu / d \lambda>0$. Obtain the corresponding equation and find the condition for $\mu$ to be affine. Deduce that, whatever parametrization $\nu$ is used along the curve $\gamma$, the tangent vector $K^{a}$ to $\gamma$ satisfies

  $$\left(\nabla_{\nu} K\right)^{[a} K^{b]}=0 \text {. }$$

  Now consider a spacetime with metric $g_{a b}$, and conformal transformation

  $$\tilde{g}_{a b}=\Omega^{2}\left(x^{c}\right) g_{a b}$$

  The curve $\gamma$ is a geodesic of the metric connection of $g_{a b}$. What further restriction has to be placed on $\gamma$ so that it is also a geodesic of the metric connection of $\tilde{g}_{a b}$ ? Justify your answer.

  comment

• Paper 2, Section II, D

  General Relativity | Part II, 2013

  A spacetime contains a one-parameter family of geodesics $x^{a}=x^{a}(\lambda, \mu)$, where $\lambda$ is a parameter along each geodesic, and $\mu$ labels the geodesics. The tangent to the geodesics is $T^{a}=\partial x^{a} / \partial \lambda$, and $N^{a}=\partial x^{a} / \partial \mu$ is a connecting vector. Prove that

  $$\nabla_{\mu} T^{a}=\nabla_{\lambda} N^{a}$$

  and hence derive the equation of geodesic deviation:

  $$\nabla_{\lambda}^{2} N^{a}+R_{b c d}^{a} T^{b} N^{c} T^{d}=0$$

  [You may assume $R_{b c d}^{a}=-R_{b d c}^{a}$ and the Ricci identity in the form

  $$\left.\left(\nabla_{\lambda} \nabla_{\mu}-\nabla_{\mu} \nabla_{\lambda}\right) T^{a}=R_{b c d}^{a} T^{b} T^{c} N^{d}\right]$$

  Consider the two-dimensional space consisting of the sphere of radius $r$ with line element

  $$d s^{2}=r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right) .$$

  Show that one may choose $T^{a}=(1,0), N^{a}=(0,1)$, and that

  $$\nabla_{\theta} N^{a}=\cot \theta N^{a} .$$

  Hence show that $R=2 / r^{2}$, using the geodesic deviation equation and the identity in any two-dimensional space

  $$R_{b c d}^{a}=\frac{1}{2} R\left(\delta_{c}^{a} g_{b d}-\delta_{d}^{a} g_{b c}\right)$$

  where $R$ is the Ricci scalar.

  Verify your answer by direct computation of $R$.

  [You may assume that the only non-zero connection components are

  $$\Gamma_{\phi \theta}^{\phi}=\Gamma_{\theta \phi}^{\phi}=\cot \theta$$

  and

  $$\Gamma_{\phi \phi}^{\theta}=-\sin \theta \cos \theta .$$

  You may also use the definition

  $$\left.R_{b c d}^{a}=\Gamma_{b d, c}^{a}-\Gamma_{b c, d}^{a}+\Gamma_{e c}^{a} \Gamma_{b d}^{e}-\Gamma_{e d}^{a} \Gamma_{b c}^{e}\right]$$

  comment

• Paper 3, Section II, D

  General Relativity | Part II, 2013

  The Schwarzschild metric for a spherically symmetric black hole is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where we have taken units in which we set $G=c=1$. Consider a photon moving within the equatorial plane $\theta=\frac{\pi}{2}$, along a path $x^{a}(\lambda)$ with affine parameter $\lambda$. Using a variational principle with Lagrangian

  $$L=g_{a b} \frac{d x^{a}}{d \lambda} \frac{d x^{b}}{d \lambda}$$

  or otherwise, show that

  $$\left(1-\frac{2 M}{r}\right)\left(\frac{d t}{d \lambda}\right)=E \quad \text { and } \quad r^{2}\left(\frac{d \phi}{d \lambda}\right)=h$$

  for constants $E$ and $h$. Deduce that

  $$\left(\frac{d r}{d \lambda}\right)^{2}=E^{2}-\frac{h^{2}}{r^{2}}\left(1-\frac{2 M}{r}\right)$$

  Assume now that the photon approaches from infinity. Show that the impact parameter (distance of closest approach) is given by

  $$b=\frac{h}{E}$$

  Denote the right hand side of equation $(*)$ as $f(r)$. By sketching $f(r)$ in each of the cases below, or otherwise, show that:

  (a) if $b^{2}>27 M^{2}$, the photon is deflected but not captured by the black hole;

  (b) if $b^{2}<27 M^{2}$, the photon is captured;

  (c) if $b^{2}=27 M^{2}$, the photon orbit has a particular form, which should be described.

  comment

• Paper 4, Section II, D

  General Relativity | Part II, 2013

  Consider the metric describing the interior of a star,

  $$d s^{2}=-e^{2 \alpha(r)} d t^{2}+e^{2 \beta(r)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  defined for $0 \leqslant r \leqslant r_{0}$ by

  $$e^{\alpha(r)}=\frac{3}{2} e^{-\beta_{0}}-\frac{1}{2} e^{-\beta(r)},$$

  with

  $$e^{-2 \beta(r)}=1-A r^{2}$$

  Here $A=2 M / r_{0}^{3}$, where $M$ is the mass of the star, $\beta_{0}=\beta\left(r_{0}\right)$, and we have taken units in which we have set $G=c=1$.

  (i) The star is made of a perfect fluid with energy-momentum tensor

  $$T_{a b}=(p+\rho) u_{a} u_{b}+p g_{a b}$$

  Here $u^{a}$ is the 4-velocity of the fluid which is at rest, the density $\rho$ is constant throughout the star $\left(0 \leqslant r \leqslant r_{0}\right)$ and the pressure $p=p(r)$ depends only on the radial coordinate. Write down the Einstein field equations and show that they may be written as

  $$R_{a b}=8 \pi(p+\rho) u_{a} u_{b}+4 \pi(\rho-p) g_{a b}$$

  (ii) Using the formulae given below, or otherwise, show that for $0 \leqslant r \leqslant r_{0}$, one has

  $$\begin{aligned} &4 \pi(\rho+p)=\frac{\left(\alpha^{\prime}+\beta^{\prime}\right)}{r} e^{-2 \beta(r)} \\ &4 \pi(\rho-p)=\left(\frac{\beta^{\prime}-\alpha^{\prime}}{r}-\frac{1}{r^{2}}\right) e^{-2 \beta(r)}+\frac{1}{r^{2}} \end{aligned}$$

  where primes denote differentiation with respect to $r$. Hence show that

  $$\rho=\frac{3 A}{8 \pi} \quad, \quad p(r)=\frac{3 A}{8 \pi}\left(\frac{e^{-\beta(r)}-e^{-\beta_{0}}}{3 e^{-\beta_{0}}-e^{-\beta(r)}}\right)$$

  [The non-zero components of the Ricci tensor are

  $$\begin{aligned} &R_{00}=e^{2 \alpha-2 \beta}\left(\alpha^{\prime \prime}-\alpha^{\prime} \beta^{\prime}+\alpha^{\prime 2}+\frac{2 \alpha^{\prime}}{r}\right) \\ &R_{11}=-\alpha^{\prime \prime}+\alpha^{\prime} \beta^{\prime}-\alpha^{\prime 2}+\frac{2 \beta^{\prime}}{r} \\ &R_{22}=1+e^{-2 \beta}\left[\left(\beta^{\prime}-\alpha^{\prime}\right) r-1\right] \\ &R_{33}=\sin ^{2} \theta R_{22} \end{aligned}$$

  Note that

  $$\left.\alpha^{\prime}=\frac{1}{2} A r e^{\beta-\alpha} \quad, \quad \beta^{\prime}=A r e^{2 \beta} .\right]$$

  comment

Geometry and Groups

• Paper 1, Section I, G

  Geometry and Groups | Part II, 2013

  Show that any pair of lines in hyperbolic 3-space that does not have a common endpoint must have a common normal. Is this still true when the pair of lines does have a common endpoint?

  comment

• Paper 1, Section II, G

  Geometry and Groups | Part II, 2013

  Define the modular group $\Gamma$ acting on the upper half-plane.

  Describe the set $S$ of points $z$ in the upper half-plane that have $\operatorname{Im}(T(z)) \leqslant \operatorname{Im}(z)$ for each $T \in \Gamma$. Hence find a fundamental set for $\Gamma$ acting on the upper half-plane.

  Let $A$ and $J$ be the two Möbius transformations

  $$A: z \mapsto z+1 \quad \text { and } \quad J: z \mapsto-1 / z$$

  When is $\operatorname{Im}(J(z))>\operatorname{Im}(z) ?$

  For any point $z$ in the upper half-plane, show that either $z \in S$ or else there is an integer $k$ with

  $$\operatorname{Im}\left(J\left(A^{k}(z)\right)\right)>\operatorname{Im}(z)$$

  Deduce that the modular group is generated by $A$ and $J$.

  comment

• Paper 2, Section I, G

  Geometry and Groups | Part II, 2013

  Let $\ell_{1}, \ell_{2}$ be two straight lines in Euclidean 3-space. Show that there is a rotation about some axis through an angle $\pi$ that maps $\ell_{1}$ onto $\ell_{2}$. Is this rotation unique?

  comment

• Paper 3, Section I, $3 G$

  Geometry and Groups | Part II, 2013

  Let $\Lambda$ be a rank 2 lattice in the Euclidean plane. Show that the group $G$ of all Euclidean isometries of the plane that map $\Lambda$ onto itself is a discrete group. List the possible sizes of the point groups for $G$ and give examples to show that point groups of these sizes do arise.

  [You may quote any standard results without proof.]

  comment

• Paper 4, Section I, $3 G$

  Geometry and Groups | Part II, 2013

  Let $\Delta_{1}, \Delta_{2}$ be two disjoint closed discs in the Riemann sphere with bounding circles $\Gamma_{1}, \Gamma_{2}$ respectively. Let $J_{k}$ be inversion in the circle $\Gamma_{k}$ and let $T$ be the Möbius transformation $J_{2} \circ J_{1}$.

  Show that, if $w \notin \Delta_{1}$, then $T(w) \in \Delta_{2}$ and so $T^{n}(w) \in \Delta_{2}$ for $n=1,2,3, \ldots$ Deduce that $T$ has a fixed point in $\Delta_{2}$ and a second in $\Delta_{1}$.

  Deduce that there is a Möbius transformation $A$ with

  $$A\left(\Delta_{1}\right)=\{z:|z| \leqslant 1\} \quad \text { and } \quad A\left(\Delta_{2}\right)=\{z:|z| \geqslant R\}$$

  for some $R>1$.

  comment

• Paper 4, Section II, $12 \mathrm{G}$

  Geometry and Groups | Part II, 2013

  Define the limit set for a Kleinian group. If your definition of the limit set requires an arbitrary choice of a base point, you should prove that the limit set does not depend on this choice.

  Let $\Delta_{1}, \Delta_{2}, \Delta_{3}, \Delta_{4}$ be the four discs $\{z \in \mathbb{C}:|z-c| \leqslant 1\}$ where $c$ is the point $1+i, 1-i,-1-i,-1+i$ respectively. Show that there is a parabolic Möbius transformation $A$ that maps the interior of $\Delta_{1}$ onto the exterior of $\Delta_{2}$ and fixes the point where $\Delta_{1}$ and $\Delta_{2}$ touch. Show further that we can choose $A$ so that it maps the unit disc onto itself.

  Let $B$ be the similar parabolic transformation that maps the interior of $\Delta_{3}$ onto the exterior of $\Delta_{4}$, fixes the point where $\Delta_{3}$ and $\Delta_{4}$ touch, and maps the unit disc onto itself. Explain why the group generated by $A$ and $B$ is a Kleinian group $G$. Find the limit set for the group $G$ and justify your answer.

  comment

Graph Theory

• Paper 1, Section II, F

  Graph Theory | Part II, 2013

  State and prove Hall's theorem about matchings in bipartite graphs.

  Show that a regular bipartite graph has a matching meeting every vertex.

  A graph is almost r-regular if each vertex has degree $r-1$ or $r$. Show that, if $r \geqslant 2$, an almost $r$-regular graph $G$ must contain an almost $(r-1)$-regular graph $H$ with $V(H)=V(G)$.

  [Hint: First, if possible, remove edges from $G$ whilst keeping it almost r-regular.]

  comment

• Paper 2, Section II, F

  Graph Theory | Part II, 2013

  Let $G$ be a graph with $|G| \geqslant 3$. State and prove a necessary and sufficient condition for $G$ to be Eulerian (that is, for $G$ to have an Eulerian circuit).

  Prove that if $\delta(G) \geqslant|G| / 2$ then $G$ is Hamiltonian (that is, $G$ has a Hamiltonian circuit).

  The line graph $L(G)$ of $G$ has vertex set $V(L(G))=E(G)$ and edge set

  $$E(L(G))=\{e f: e, f \in E(G), e \text { and } f \text { are incident }\} .$$

  Show that $L(G)$ is Eulerian if $G$ is regular and connected.

  Must $L(G)$ be Hamiltonian if $G$ is Eulerian? Must $G$ be Eulerian if $L(G)$ is Hamiltonian? Justify your answers.

  comment

• Paper 3, Section II, F

  Graph Theory | Part II, 2013

  Let $G$ be a graph of order $n$ and average degree $d$. Let $A$ be the adjacency matrix of $G$ and let $x^{n}+c_{1} x^{n-1}+c_{2} x^{n-2}+\cdots+c_{n}$ be its characteristic polynomial. Show that $c_{1}=0$ and $c_{2}=-n d / 2$. Show also that $-c_{3}$ is twice the number of triangles in $G$.

  The eigenvalues of $A$ are $\lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{n}$. Prove that $\lambda_{1} \geqslant d$.

  Evaluate $\lambda_{1}+\cdots+\lambda_{n}$. Show that $\lambda_{1}^{2}+\cdots+\lambda_{n}^{2}=n d$ and infer that $\lambda_{1} \leqslant \sqrt{d(n-1)}$. Does there exist, for each $n$, a graph $G$ with $d>0$ for which $\lambda_{2}=\cdots=\lambda_{n}$ ?

  comment

• Paper 4, Section II, F

  Graph Theory | Part II, 2013

  Define the maximum degree $\Delta(G)$ and the chromatic index $\chi^{\prime}(G)$ of the graph $G$.

  State and prove Vizing's theorem relating $\Delta(G)$ and $\chi^{\prime}(G)$.

  Let $G$ be a connected graph such that $\chi^{\prime}(G)=\Delta(G)+1$ but, for every subgraph $H$ of $G, \chi^{\prime}(H)=\Delta(H)$ holds. Show that $G$ is a circuit of odd length.

  comment

Integrable Systems

• Paper 1, Section II, C

  Integrable Systems | Part II, 2013

  Quoting carefully all necessary results, use the theory of inverse scattering to derive the 1-soliton solution of the $\mathrm{KdV}$ equation

  $$u_{t}=6 u u_{x}-u_{x x x}$$

  comment

• Paper 2, Section II, 32C

  Integrable Systems | Part II, 2013

  Consider the Hamiltonian system

  $$\mathbf{p}^{\prime}=-\frac{\partial H}{\partial \mathbf{q}}, \quad \mathbf{q}^{\prime}=\frac{\partial H}{\partial \mathbf{p}}$$

  where $H=H(\mathbf{p}, \mathbf{q})$.

  When is the transformation $\mathbf{P}=\mathbf{P}(\mathbf{p}, \mathbf{q}), \mathbf{Q}=\mathbf{Q}(\mathbf{p}, \mathbf{q})$ canonical?

  Prove that, if the transformation is canonical, then the equations in the new variables $(\mathbf{P}, \mathbf{Q})$ are also Hamiltonian, with the same Hamiltonian function $H$.

  Let $\mathbf{P}=C^{-1} \mathbf{p}+B q, \mathbf{Q}=C \mathbf{q}$, where $C$ is a symmetric nonsingular matrix. Determine necessary and sufficient conditions on $C$ for the transformation to be canonical.

  comment

• Paper 3, Section II, C

  Integrable Systems | Part II, 2013

  Let $U=U(x, y)$ and $V=V(x, y)$ be two $n \times n$ complex-valued matrix functions, smoothly differentiable in their variables. We wish to explore the solution of the overdetermined linear system

  $$\frac{\partial \mathbf{v}}{\partial y}=U(x, y) \mathbf{v}, \quad \frac{\partial \mathbf{v}}{\partial x}=V(x, y) \mathbf{v}$$

  for some twice smoothly differentiable vector function $\mathbf{v}(x, y)$.

  Prove that, if the overdetermined system holds, then the functions $U$ and $V$ obey the zero curvature representation

  $$\frac{\partial U}{\partial x}-\frac{\partial V}{\partial y}+U V-V U=0$$

  Let $u=u(x, y)$ and

  $$U=\left[\begin{array}{cc} i \lambda & i \bar{u} \\ i u & -i \lambda \end{array}\right], \quad V=\left[\begin{array}{cc} 2 i \lambda^{2}-i|u|^{2} & 2 i \lambda \bar{u}+\bar{u}_{y} \\ 2 i \lambda u-u_{y} & -2 i \lambda^{2}+i|u|^{2} \end{array}\right]$$

  where subscripts denote derivatives, $\bar{u}$ is the complex conjugate of $u$ and $\lambda$ is a constant. Find the compatibility condition on the function $u$ so that $U$ and $V$ obey the zero curvature representation.

  comment

Linear Analysis

• Paper 1, Section II, F

  Linear Analysis | Part II, 2013

  State and prove the Closed Graph Theorem. [You may assume any version of the Baire Category Theorem provided it is clearly stated. If you use any other result from the course, then you must prove it.]

  Let $X$ be a closed subspace of $\ell_{\infty}$ such that $X$ is also a subset of $\ell_{1}$. Show that the left-shift $L: X \rightarrow \ell_{1}$, given by $L\left(x_{1}, x_{2}, x_{3}, \ldots\right)=\left(x_{2}, x_{3}, \ldots\right)$, is bounded when $X$ is equipped with the sup-norm.

  comment

• Paper 2, Section II, F

  Linear Analysis | Part II, 2013

  Let $X$ be a Banach space. Let $T: X \rightarrow \ell_{\infty}$ be a bounded linear operator. Show that there is a bounded sequence $\left(f_{n}\right)_{n=1}^{\infty}$ in $X^{*}$ such that $T x=\left(f_{n} x\right)_{n=1}^{\infty}$ for all $x \in X$.

  Fix $1<p<\infty$. Define the Banach space $\ell_{p}$ and briefly explain why it is separable. Show that for $x \in \ell_{p}$ there exists $f \in \ell_{p}^{*}$ such that $\|f\|=1$ and $f(x)=\|x\|_{p}$. [You may use Hölder's inequality without proof.]

  Deduce that $\ell_{p}$ embeds isometrically into $\ell_{\infty}$.

  comment

• Paper 3, Section II, F

  Linear Analysis | Part II, 2013

  State the Stone-Weierstrass Theorem for real-valued functions.

  State Riesz's Lemma.

  Let $K$ be a compact, Hausdorff space and let $A$ be a subalgebra of $C(K)$ separating the points of $K$ and containing the constant functions. Fix two disjoint, non-empty, closed subsets $E$ and $F$ of $K$.

  (i) If $x \in E$ show that there exists $g \in A$ such that $g(x)=0,0 \leqslant g<1$ on $K$, and $g>0$ on $F$. Explain briefly why there is $M \in \mathbb{N}$ such that $g \geqslant \frac{2}{M}$ on $F$.

  (ii) Show that there is an open cover $U_{1}, U_{2}, \ldots, U_{m}$ of $E$, elements $g_{1}, g_{2}, \ldots, g_{m}$ of $A$ and positive integers $M_{1}, M_{2}, \ldots, M_{m}$ such that

  $$0 \leqslant g_{r}<1 \text { on } K, \quad g_{r} \geqslant \frac{2}{M_{r}} \text { on } F, \quad g_{r}<\frac{1}{2 M_{r}} \text { on } U_{r}$$

  for each $r=1,2, \ldots, m$.

  (iii) Using the inequality

  $$1-N t \leqslant(1-t)^{N} \leqslant \frac{1}{N t} \quad(0<t<1, N \in \mathbb{N})$$

  show that for sufficiently large positive integers $n_{1}, n_{2}, \ldots, n_{m}$, the element

  $$h_{r}=1-\left(1-g_{r}^{n_{r}}\right)^{M_{r}^{n_{r}}}$$

  of $A$ satisfies

  $$0 \leqslant h_{r} \leqslant 1 \text { on } K, \quad h_{r} \leqslant \frac{1}{4} \text { on } U_{r}, \quad h_{r} \geqslant\left(\frac{3}{4}\right)^{\frac{1}{m}} \text { on } F$$

  for each $r=1,2, \ldots, m$.

  (iv) Show that the element $h=h_{1} \cdot h_{2} \cdots \cdot h_{m}-\frac{1}{2}$ of $A$ satisfies

  $$-\frac{1}{2} \leqslant h \leqslant \frac{1}{2} \text { on } K, \quad h \leqslant-\frac{1}{4} \text { on } E, \quad h \geqslant \frac{1}{4} \text { on } F \text {. }$$

  Now let $f \in C(K)$ with $\|f\| \leqslant 1$. By considering the sets $\left\{x \in K: f(x) \leqslant-\frac{1}{4}\right\}$ and $\left\{x \in K: f(x) \geqslant \frac{1}{4}\right\}$, show that there exists $h \in A$ such that $\|f-h\| \leqslant \frac{3}{4}$. Deduce that $A$ is dense in $C(K)$.

  comment

• Paper 4, Section II, F

  Linear Analysis | Part II, 2013

  Let $T: X \rightarrow X$ be a bounded linear operator on a complex Banach space $X$. Define the spectrum $\sigma(T)$ of $T$. What is an approximate eigenvalue of $T$ ? What does it mean to say that $T$ is compact?

  Assume now that $T$ is compact. Show that if $\lambda$ is in the boundary of $\sigma(T)$ and $\lambda \neq 0$, then $\lambda$ is an eigenvalue of $T$. [You may use without proof the result that every $\lambda$ in the boundary of $\sigma(T)$ is an approximate eigenvalue of $T$.]

  Let $T: H \rightarrow H$ be a compact Hermitian operator on a complex Hilbert space $H$. Prove the following:

  (a) If $\lambda \in \sigma(T)$ and $\lambda \neq 0$, then $\lambda$ is an eigenvalue of $T$.

  (b) $\sigma(T)$ is countable.

  comment

Logic and Set Theory

• Paper 1, Section II, G

  Logic and Set Theory | Part II, 2013

  Write down the recursive definitions of ordinal addition, multiplication and exponentiation.

  Given that $F: \mathbf{O n} \rightarrow \mathbf{O n}$ is a strictly increasing function-class (i.e. $\alpha<\beta$ implies $F(\alpha)<F(\beta))$, show that $\alpha \leqslant F(\alpha)$ for all $\alpha$.

  Show that every ordinal $\alpha$ has a unique representation in the form

  $$\alpha=\omega^{\alpha_{1}} \cdot a_{1}+\omega^{\alpha_{2}} \cdot a_{2}+\cdots+\omega^{\alpha_{n}} \cdot a_{n}$$

  where $n \in \omega, \alpha \geqslant \alpha_{1}>\alpha_{2}>\cdots>\alpha_{n}$, and $a_{1}, a_{2}, \ldots, a_{n} \in \omega \backslash\{0\}$.

  Under what conditions can an ordinal $\alpha$ be represented in the form

  $$\omega^{\beta_{1}} \cdot b_{1}+\omega^{\beta_{2}} \cdot b_{2}+\cdots+\omega^{\beta_{m}} \cdot b_{m}$$

  where $\beta_{1}<\beta_{2}<\cdots<\beta_{m}$ and $b_{1}, b_{2}, \ldots, b_{m} \in \omega \backslash\{0\} ?$ Justify your answer.

  [The laws of ordinal arithmetic (associative, distributive, etc.) may be assumed without proof.]

  comment

• Paper 2, Section II, G

  Logic and Set Theory | Part II, 2013

  Explain what is meant by a chain-complete poset. State the Bourbaki-Witt fixedpoint theorem for such posets.

  A poset $P$ is called directed if every finite subset of $P$ (including the empty subset) has an upper bound in $P ; P$ is called directed-complete if every subset of $P$ which is directed (in the induced ordering) has a least upper bound in $P$. Show that the set of all chains in an arbitrary poset $P$, ordered by inclusion, is directed-complete.

  Given a poset $P$, let $[P \rightarrow P]$ denote the set of all order-preserving maps $P \rightarrow P$, ordered pointwise (i.e. $f \leqslant g$ if and only if $f(x) \leqslant g(x)$ for all $x$ ). Show that $[P \rightarrow P]$ is directed-complete if $P$ is.

  Now suppose $P$ is directed-complete, and that $f: P \rightarrow P$ is order-preserving and inflationary. Show that there is a unique smallest set $C \subseteq[P \rightarrow P]$ satisfying

  (a) $f \in C$;

  (b) $C$ is closed under composition (i.e. $g, h \in C \Rightarrow g \circ h \in C$ ); and

  (c) $C$ is closed under joins of directed subsets.

  Show that

  (i) all maps in $C$ are inflationary;

  (ii) $C$ is directed;

  (iii) if $g=\bigvee C$, then all values of $g$ are fixed points of $f$;

  (iv) for every $x \in P$, there exists $y \in P$ with $x \leqslant y=f(y)$.

  comment

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2013

  Explain carefully what is meant by syntactic entailment and semantic entailment in the propositional calculus. State the Completeness Theorem for the propositional calculus, and deduce the Compactness Theorem.

  Suppose $P, Q$ and $R$ are pairwise disjoint sets of primitive propositions, and let $\phi \in \mathcal{L}(P \cup Q)$ and $\psi \in \mathcal{L}(Q \cup R)$ be propositional formulae such that $(\phi \Rightarrow \psi)$ is a theorem of the propositional calculus. Consider the set

  $$X=\{\chi \in \mathcal{L}(Q) \mid \phi \vdash \chi\}$$

  Show that $X \cup\{\neg \psi\}$ is inconsistent, and deduce that there exists $\chi \in \mathcal{L}(Q)$ such that both $(\phi \Rightarrow \chi)$ and $(\chi \Rightarrow \psi)$ are theorems. [Hint: assuming $X \cup\{\neg \psi\}$ is consistent, take a suitable valuation $v$ of $Q \cup R$ and show that

  $$\{\phi\} \cup\{q \in Q \mid v(q)=1\} \cup\{\neg q \mid q \in Q, v(q)=0\}$$

  is inconsistent. The Deduction Theorem may be assumed without proof.]

  comment

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2013

  State the Axiom of Foundation and the Principle of $\in$-Induction, and show that they are equivalent in the presence of the other axioms of ZF set theory. [You may assume the existence of transitive closures.]

  Given a model $(V, \in)$ for all the axioms of ZF except Foundation, show how to define a transitive class $R$ which, with the restriction of the given relation $\in$, is a model of ZF.

  Given a model $(V, \in)$ of $\mathrm{ZF}$, indicate briefly how one may modify the relation $\in$ so that the resulting structure $\left(V, \in^{\prime}\right)$ fails to satisfy Foundation, but satisfies all the other axioms of $\mathrm{ZF}$. [You need not verify that all the other axioms hold in $\left(V, \in^{\prime}\right)$.]

  comment

Mathematical Biology

• Paper 1, Section I, A

  Mathematical Biology | Part II, 2013

  In a discrete-time model, a proportion $\mu$ of mature bacteria divides at each time step. When a mature bacterium divides it is destroyed and two new immature bacteria are produced. A proportion $\lambda$ of the immature bacteria matures at each time step, and a proportion $k$ of mature bacteria dies at each time step. Show that this model may be represented by the equations

  $$\begin{aligned} &a_{t+1}=a_{t}+2 \mu b_{t}-\lambda a_{t} \\ &b_{t+1}=b_{t}-\mu b_{t}+\lambda a_{t}-k b_{t} \end{aligned}$$

  Give an expression for the general solution to these equations and show that the population may grow if $\mu>k$.

  At time $T$, the population is treated with an antibiotic that completely stops bacteria from maturing, but otherwise has no direct effects. Explain what will happen to the population of bacteria afterwards, and give expressions for $a_{t}$ and $b_{t}$ for $t>T$ in terms of $a_{T}, b_{T}, \mu$ and $k$.

  comment

• Paper 2, Section I, A

  Mathematical Biology | Part II, 2013

  The population density $n(a, t)$ of individuals of age $a$ at time $t$ satisfies

  $$\frac{\partial n(a, t)}{\partial t}+\frac{\partial n(a, t)}{\partial a}=-\mu(a) n(a, t)$$

  with

  $$n(0, t)=\int_{0}^{\infty} b(a) n(a, t) d a$$

  where $\mu(a)$ is the age-dependent death rate and $b(a)$ is the birth rate per individual of age

  Seek a similarity solution of the form $n(a, t)=e^{\gamma t} r(a)$ and show that

  $$r(a)=r(0) e^{-\gamma a-\int_{0}^{a} \mu(s) d s}, \quad r(0)=\int_{0}^{\infty} b(s) r(s) d s .$$

  Show also that if

  $$\phi(\gamma)=\int_{0}^{\infty} b(a) e^{-\gamma a-\int_{0}^{a} \mu(s) d s} d a=1$$

  then there is such a similarity solution. Give a biological interpretation of $\phi(0)$.

  Suppose now that all births happen at age $a^{*}$, at which time an individual produces $B$ offspring, and that the death rate is constant with age (i.e. $\mu(a)=\mu)$. Find the similarity solution and give the condition for this to represent a growing population.

  comment

• Paper 2, Section II, A

  Mathematical Biology | Part II, 2013

  The concentration $c(x, t)$ of insects at position $x$ at time $t$ satisfies the nonlinear diffusion equation

  $$\frac{\partial c}{\partial t}=\frac{\partial}{\partial x}\left(c^{m} \frac{\partial c}{\partial x}\right)$$

  with $m>0$. Find the value of $\alpha$ which allows a similarity solution of the form $c(x, t)=t^{\alpha} f(\xi)$, with $\xi=t^{\alpha} x$.

  Show that

  $$f(\xi)=\left\{\begin{array}{cl} {\left[\frac{\alpha m}{2}\left(\xi^{2}-\xi_{0}^{2}\right)\right]^{1 / m}} & \text { for }-\xi_{0}<\xi<\xi_{0} \\ 0 & \text { otherwise } \end{array}\right.$$

  where $\xi_{0}$ is a constant. From the original partial differential equation, show that the total number of insects $c_{0}$ does not change in time. From this result, find a general expression relating $\xi_{0}$ and $c_{0}$. Find a closed-form solution for $\xi_{0}$ in the case $m=2$.

  comment

• Paper 3, Section I, A

  Mathematical Biology | Part II, 2013

  An immune system creates a burst of $N$ new white blood cells with probability $b$ per unit time. White blood cells die with probability $d$ each per unit time. Write down the master equation for $P_{n}(t)$, the probability that there are $n$ white blood cells at time $t$.

  Given that $n=n_{0}$ initially, find an expression for the mean of $n$.

  Show that the variance of $n$ has the form $A e^{-2 d t}+B e^{-d t}+C$ and find $A, B$ and $C$.

  If the immune system were modified to produce $k$ times as many cells per burst but with probability per unit time divided by a factor $k$, how would the mean and variance of the number of cells change?

  comment

• Paper 3, Section II, A

  Mathematical Biology | Part II, 2013

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} &\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}+u-u v+a u^{2} \\ &\frac{\partial v}{\partial t}=d \frac{\partial^{2} v}{\partial x^{2}}+u^{2}-b u v \end{aligned}$$

  where $a, b, d>0$.

  Find and sketch the range of $a, b$ for which the spatially homogeneous system has a stable stationary solution with $u>0$ and $v>0$.

  Considering spatial perturbations of the form $\cos (k x)$ about the solution found above, find conditions for the system to be unstable. Sketch this region in the $(d, b)$ plane for fixed $a \in(0,1)$.

  Find $k_{c}$, the critical wavenumber at the onset of the instability, in terms of $a$ and $b$.

  comment

• Paper 4, Section I, A

  Mathematical Biology | Part II, 2013

  A model of two populations competing for resources takes the form

  $$\begin{aligned} \frac{d n_{1}}{d t} &=r_{1} n_{1}\left(1-n_{1}-a_{12} n_{2}\right) \\ \frac{d n_{2}}{d t} &=r_{2} n_{2}\left(1-n_{2}-a_{21} n_{1}\right) \end{aligned}$$

  where all parameters are positive. Give a brief biological interpretation of $a_{12}, a_{21}, r_{1}$ and $r_{2}$. Briefly describe the dynamics of each population in the absence of the other.

  Give conditions for there to exist a steady-state solution with both populations present (that is, $n_{1}>0$ and $n_{2}>0$ ), and give conditions for this solution to be stable.

  In the case where there exists a solution with both populations present but the solution is not stable, what is the likely long-term outcome for the biological system? Explain your answer with the aid of a phase diagram in the $\left(n_{1}, n_{2}\right)$ plane.

  comment

Number Fields

• Paper 1, Section II, H

  Number Fields | Part II, 2013

  Let $f \in \mathbb{Z}[X]$ be a monic irreducible polynomial of degree $n$. Let $K=\mathbb{Q}(\alpha)$, where $\alpha$ is a root of $f$.

  (i) Show that if $\operatorname{disc}(f)$ is square-free then $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$.

  (ii) In the case $f(X)=X^{3}-3 X-25$ find the minimal polynomial of $\beta=3 /(1-\alpha)$ and hence compute the discriminant of $K$. What is the index of $\mathbb{Z}[\alpha]$ in $\mathcal{O}_{K}$ ?

  [Recall that the discriminant of $X^{3}+p X+q$ is $-4 p^{3}-27 q^{2}$.]

  comment

• Paper 2, Section II, H

  Number Fields | Part II, 2013

  (i) State Dirichlet's unit theorem.

  (ii) Let $K$ be a number field. Show that if every conjugate of $\alpha \in \mathcal{O}_{K}$ has absolute value at most 1 then $\alpha$ is either zero or a root of unity.

  (iii) Let $k=\mathbb{Q}(\sqrt{3})$ and $K=\mathbb{Q}(\zeta)$ where $\zeta=e^{i \pi / 6}=(i+\sqrt{3}) / 2$. Compute $N_{K / k}(1+\zeta)$. Show that

  $$\mathcal{O}_{K}^{*}=\left\{(1+\zeta)^{m} u: 0 \leqslant m \leqslant 11, u \in \mathcal{O}_{k}^{*}\right\}$$

  Hence or otherwise find fundamental units for $k$ and $K$.

  [You may assume that the only roots of unity in $K$ are powers of $\zeta .$ ]

  comment

• Paper 4, Section II, H

  Number Fields | Part II, 2013

  State Dedekind's criterion. Use it to factor the primes up to 5 in the ring of integers $\mathcal{O}_{K}$ of $K=\mathbb{Q}(\sqrt{65})$. Show that every ideal in $\mathcal{O}_{K}$ of norm 10 is principal, and compute the class group of $K$.

  comment

Number Theory

• Paper 1, Section I, I

  Number Theory | Part II, 2013

  State and prove Gauss's Lemma for the Legendre symbol $\left(\frac{a}{p}\right)$. For which odd primes $p$ is 2 a quadratic residue modulo $p ?$ Justify your answer.

  comment

• Paper 2, Section I, I

  Number Theory | Part II, 2013

  Define Euler's totient function $\phi(n)$, and show that $\sum_{d \mid n} \phi(d)=n$. Hence or otherwise prove that for any prime $p$ the multiplicative group $(\mathbb{Z} / p \mathbb{Z})^{\times}$is cyclic.

  comment

• Paper 3, Section I, I

  Number Theory | Part II, 2013

  State the Chinese Remainder Theorem.

  A composite number $n$ is defined to be a Carmichael number if $b^{n-1} \equiv 1 \bmod n$ whenever $(b, n)=1$. Show that a composite $n$ is Carmichael if and only if $n$ is square-free and $(p-1)$ divides $(n-1)$ for all prime factors $p$ of $n$. [You may assume that, for $p$ an odd prime and $\alpha \geqslant 1$ an integer, $\left(\mathbb{Z} / p^{\alpha} \mathbb{Z}\right)^{\times}$is a cyclic group.]

  Show that if $n=(6 t+1)(12 t+1)(18 t+1)$ with all three factors prime, then $n$ is Carmichael.

  comment

• Paper 3, Section II, I

  Number Theory | Part II, 2013

  Define equivalence of binary quadratic forms and show that equivalent forms have the same discriminant.

  Show that an integer $n$ is properly represented by a binary quadratic form of discriminant $d$ if and only if $x^{2} \equiv d \bmod 4 n$ is soluble in integers. Which primes are represented by a form of discriminant $-20$ ?

  What does it mean for a positive definite form to be reduced? Find all reduced forms of discriminant $-20$. For each member of your list find the primes less than 100 represented by the form.

  comment

• Paper 4, Section I, I

  Number Theory | Part II, 2013

  Let $s=\sigma+i t$ with $\sigma, t \in \mathbb{R}$. Define the Riemann zeta function $\zeta(s)$ for $\sigma>1$. Show that for $\sigma>1$,

  $$\zeta(s)=\prod_{p}\left(1-p^{-s}\right)^{-1}$$

  where the product is taken over all primes. Deduce that there are infinitely many primes.

  comment

• Paper 4, Section II, I

  Number Theory | Part II, 2013

  (i) What is meant by the continued fraction expansion of a real number $\theta$ ? Suppose that $\theta$ has continued fraction $\left[a_{0}, a_{1}, a_{2}, \ldots\right]$. Define the convergents $p_{n} / q_{n}$ to $\theta$ and give the recurrence relations satisfied by the $p_{n}$ and $q_{n}$. Show that the convergents $p_{n} / q_{n}$ do indeed converge to $\theta$.

  [You need not justify the basic order properties of finite continued fractions.]

  (ii) Find two solutions in strictly positive integers to each of the equations

  $$x^{2}-10 y^{2}=1 \quad \text { and } \quad x^{2}-11 y^{2}=1$$

  comment

Numerical Analysis

• Paper 1, Section II, 40C

  Numerical Analysis | Part II, 2013

  Let

  $$A(\alpha)=\left(\begin{array}{ccc} 1 & \alpha & \alpha \\ \alpha & 1 & \alpha \\ \alpha & \alpha & 1 \end{array}\right), \quad \alpha \in \mathbb{R}$$

  (i) For which values of $\alpha$ is $A(\alpha)$ positive definite?

  (ii) Formulate the Gauss-Seidel method for the solution $\mathbf{x} \in \mathbb{R}^{3}$ of a system

  $$A(\alpha) \mathbf{x}=\mathbf{b}$$

  with $A(\alpha)$ as defined above and $\mathbf{b} \in \mathbb{R}^{3}$. Prove that the Gauss-Seidel method converges to the solution of the above system whenever $A$ is positive definite. [You may state and use the Householder-John theorem without proof.]

  (iii) For which values of $\alpha$ does the Jacobi iteration applied to the solution of the above system converge?

  comment

• Paper 2, Section II, C

  Numerical Analysis | Part II, 2013

  Consider the advection equation $u_{t}=u_{x}$ on the unit interval $x \in[0,1]$ and $t \geqslant 0$, where $u=u(x, t)$, subject to the initial condition $u(x, 0)=\varphi(x)$ and the boundary condition $u(1, t)=0$, where $\varphi$ is a given smooth function on $[0,1]$.

  (i) We commence by discretising the advection equation above with finite differences on the equidistant space-time grid $\{(m \Delta x, n \Delta t), m=0, \ldots, M+1, n=0, \ldots, T\}$ with $\Delta x=1 /(M+1)$ and $\Delta t>0$. We obtain an equation for $u_{m}^{n} \approx u(m \Delta x, n \Delta t)$ that reads

  $$u_{m}^{n+1}=u_{m}^{n}+\frac{1}{2} \mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right), \quad m=1, \ldots, M, n \in \mathbb{Z}^{+}$$

  with the condition $u_{0}^{n}=0$ for all $n \in \mathbb{Z}^{+}$and $\mu=\Delta t / \Delta x$.

  What is the order of approximation (that is, the order of the local error) in space and time of the above discrete solution to the exact solution of the advection equation? Write the scheme in matrix form and deduce for which choices of $\mu$ this approximation converges to the exact solution. State (without proof) any theorems you use. [You may use the fact that for a tridiagonal $M \times M$ matrix

  $$\left(\begin{array}{cccc} \alpha & \beta & 0 & 0 \\ -\beta & \ddots & \ddots & 0 \\ 0 & \ddots & \ddots & \beta \\ 0 & 0 & -\beta & \alpha \end{array}\right)$$

  the eigenvalues are given by $\lambda_{\ell}=\alpha+2 i \beta \cos \frac{\ell \pi}{M+1}$.]

  (ii) How does the order change when we replace the central difference approximation of the first derivative in space by forward differences, that is $u_{m+1}^{n}-u_{m}^{n}$ instead of $\left(u_{m+1}^{n}-u_{m-1}^{n}\right) / 2 ?$ For which choices of $\mu$ is this new scheme convergent?

  (iii) Instead of the approximation in (i) we consider the following method for numerically solving the advection equation,

  $$u_{m}^{n+1}=\mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right)+u_{m}^{n-1}$$

  where we additionally assume that $u_{m}^{1}$ is given. What is the order of this method for a fixed $\mu$ ?

  comment

• Paper 3, Section II, C

  Numerical Analysis | Part II, 2013

  (i) Suppose that $A$ is a real $n \times n$ matrix, and that $\mathbf{w} \in \mathbb{R}^{n}$ and $\lambda_{1} \in \mathbb{R}$ are given so that $A \mathbf{w}=\lambda_{1} \mathbf{w}$. Further, let $S$ be a non-singular matrix such that $S \mathbf{w}=c \mathbf{e}_{1}$, where $\mathbf{e}_{1}$ is the first coordinate vector and $c \neq 0$. Let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are $\lambda_{1}$ together with the eigenvalues of the bottom right $(n-1) \times(n-1)$ submatrix of $\widehat{A}$.

  (ii) Suppose again that $A$ is a real $n \times n$ matrix, and that two linearly independent vectors $\mathbf{v}, \mathbf{w} \in \mathbb{R}^{n}$ are given such that the linear subspace $\mathcal{L}\{\mathbf{v}, \mathbf{w}\}$ spanned by $\mathbf{v}$ and $w$ is invariant under the action of $A$, that is

  $$x \in \mathcal{L}\{\mathbf{v}, \mathbf{w}\} \quad \Rightarrow \quad A x \in \mathcal{L}\{\mathbf{v}, \mathbf{w}\} .$$

  Denote by $V$ an $n \times 2$ matrix whose two columns are the vectors $\mathbf{v}$ and $\mathbf{w}$, and let $S$ be a non-singular matrix such that $R=S V$ is upper triangular, that is

  $$R=S V=S \times\left(\begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \\ \vdots & \vdots \\ v_{n} & w_{n} \end{array}\right)=\left(\begin{array}{cc} r_{11} & r_{12} \\ 0 & r_{22} \\ 0 & 0 \\ \vdots & \vdots \\ 0 & 0 \end{array}\right)$$

  Again, let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are the eigenvalues of the top left $2 \times 2$ submatrix of $\widehat{A}$together with the eigenvalues of the bottom right $(n-2) \times(n-2)$ submatrix of $\widehat{A} .$

  comment

• Paper 4, Section II, C

  Numerical Analysis | Part II, 2013

  Consider the solution of the two-point boundary value problem

  $$(2-\sin \pi x) u^{\prime \prime}+u=1, \quad-1 \leqslant x \leqslant 1$$

  with periodic boundary conditions at $x=-1$ and $x=1$. Construct explicitly the linear algebraic system that arises from the application of a spectral method to the above equation.

  The Fourier coefficients of $u$ are defined by

  $$\hat{u}_{n}=\frac{1}{2} \int_{-1}^{1} u(\tau) e^{-i \pi n \tau} d \tau$$

  Prove that the computation of the Fourier coefficients for the truncated system with $-N / 2+1 \leqslant n \leqslant N / 2$ (where $N$ is an even and positive integer, and assuming that $\hat{u}_{n}=0$ outside this range of $n$ ) reduces to the solution of a tridiagonal system of algebraic equations, which you should specify.

  Explain the term convergence with spectral speed and justify its validity for the derived approximation of $u$.

  comment

Optimization and Control

• Paper 2, Section II, K

  Optimization and Control | Part II, 2013

  Suppose $\left\{x_{t}\right\}_{t \geqslant 0}$ is a Markov chain. Consider the dynamic programming equation

  $$F_{s}(x)=\max \left\{r(x), \beta E\left[F_{s-1}\left(x_{1}\right) \mid x_{0}=x\right]\right\}, \quad s=1,2, \ldots,$$

  with $r(x)>0, \beta \in(0,1)$, and $F_{0}(x)=0$. Prove that:

  (i) $F_{s}(x)$ is nondecreasing in $s$;

  (ii) $F_{s}(x) \leqslant F(x)$, where $F(x)$ is the value function of an infinite-horizon problem that you should describe;

  (iii) $F_{\infty}(x)=\lim _{s \rightarrow \infty} F_{s}(x)=F(x)$.

  A coin lands heads with probability $p$. A statistician wishes to choose between: $H_{0}: p=1 / 3$ and $H_{1}: p=2 / 3$, one of which is true. Prior probabilities of $H_{1}$ and $H_{0}$ in the ratio $x: 1$ change after one toss of the coin to ratio $2 x: 1$ (if the toss was a head) or to ratio $x: 2$ (if the toss was a tail). What problem is being addressed by the following dynamic programming equation?

  $$F(x)=\max \left\{\frac{1}{1+x}, \frac{x}{1+x}, \beta\left[\left(\frac{1}{1+x} \frac{2}{3}+\frac{x}{1+x} \frac{1}{3}\right) F(x / 2)+\left(\frac{1}{1+x} \frac{1}{3}+\frac{x}{1+x} \frac{2}{3}\right) F(2 x)\right]\right\}$$

  Prove that $G(x)=(1+x) F(x)$ is a convex function of $x$.

  By sketching a graph of $G$, describe the form of the optimal policy.

  comment

• Paper 3, Section II, K

  Optimization and Control | Part II, 2013

  A particle follows a discrete-time trajectory in $\mathbb{R}^{2}$ given by

  $$\left(\begin{array}{l} x_{t+1} \\ y_{t+1} \end{array}\right)=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)\left(\begin{array}{l} x_{t} \\ y_{t} \end{array}\right)+\left(\begin{array}{c} t \\ 1 \end{array}\right) u_{t}+\left(\begin{array}{c} \epsilon_{t} \\ 0 \end{array}\right)$$

  where $\left\{\epsilon_{t}\right\}$ is a white noise sequence with $E \epsilon_{t}=0$ and $E \epsilon_{t}^{2}=v$. Given $\left(x_{0}, y_{0}\right)$, we wish to choose $\left\{u_{t}\right\}_{t=0}^{9}$ to minimize $C=E\left[x_{10}^{2}+\sum_{t=0}^{9} u_{t}^{2}\right]$.

  Show that for some $\left\{a_{t}\right\}$ this problem can be reduced to one of controlling a scalar state $\xi_{t}=x_{t}+a_{t} y_{t}$.

  Find, in terms of $x_{0}, y_{0}$, the optimal $u_{0}$. What is the change in minimum $C$ achievable when the system starts in $\left(x_{0}, y_{0}\right)$ as compared to when it starts in $(0,0)$ ?

  Consider now a trajectory starting at $\left(x_{-1}, y_{-1}\right)=(11,-1)$. What value of $u_{-1}$ is optimal if we wish to minimize $5 u_{-1}^{2}+C$ ?

  comment

• Paper 4, Section II, K

  Optimization and Control | Part II, 2013

  Given $r, \rho, \mu, T$, all positive, it is desired to choose $u(t)>0$ to maximize

  $$\mu x(T)+\int_{0}^{T} e^{-\rho t} \log u(t) d t$$

  subject to $\dot{x}(t)=r x(t)-u(t), x(0)=10$.

  Explain what Pontryagin's maximum principle guarantees about a solution to this problem.

  Show that no matter whether $x(T)$ is constrained or unconstrained there is a constant $\alpha$ such that the optimal control is of the form $u(t)=\alpha e^{-(\rho-r) t}$. Find an expression for $\alpha$ under the constraint $x(T)=5$.

  Show that if $x(T)$ is unconstrained then $\alpha=(1 / \mu) e^{-r T}$.

  comment

Partial Differential Equations

• Paper 1, Section II, C

  Partial Differential Equations | Part II, 2013

  (i) Discuss briefly the concept of well-posedness of a Cauchy problem for a partial differential equation.

  Solve the Cauchy problem

  $$\partial_{2} u+x_{1} \partial_{1} u=a u^{2}, \quad u\left(x_{1}, 0\right)=\phi\left(x_{1}\right),$$

  where $a \in \mathbb{R}, \phi \in C^{1}(\mathbb{R})$ and $\partial_{i}$ denotes the partial derivative with respect to $x_{i}$ for $i=1,2$.

  For the case $a=0$ show that the solution satisfies $\max _{x_{1} \in \mathbb{R}}\left|u\left(x_{1}, x_{2}\right)\right|=\|\phi\|_{C^{0}}$, where the $C^{r}$ norm on functions $\phi=\phi\left(x_{1}\right)$ of one variable is defined by

  $$\|\phi\|_{C^{r}}=\sum_{i=0}^{r} \max _{x \in \mathbb{R}}\left|\partial_{1}^{i} \phi\left(x_{1}\right)\right|$$

  Deduce that the Cauchy problem is then well-posed in the uniform metric (i.e. the metric determined by the $C^{0}$ norm).

  (ii) State the Cauchy-Kovalevskaya theorem and deduce that the following Cauchy problem for the Laplace equation,

  $$\partial_{1}^{2} u+\partial_{2}^{2} u=0, \quad u\left(x_{1}, 0\right)=0, \partial_{2} u\left(x_{1}, 0\right)=\phi\left(x_{1}\right)$$

  has a unique analytic solution in some neighbourhood of $x_{2}=0$ for any analytic function $\phi=\phi\left(x_{1}\right)$. Write down the solution for the case $\phi\left(x_{1}\right)=\sin \left(n x_{1}\right)$, and hence give a sequence of initial data $\left\{\phi_{n}\left(x_{1}\right)\right\}_{n=1}^{\infty}$ with the property that

  $$\left\|\phi_{n}\right\|_{C^{r}} \rightarrow 0, \quad \text { as } n \rightarrow \infty, \text { for each } r \in \mathbb{N},$$

  whereas $u_{n}$, the corresponding solution of $(*)$, satisfies

  $$\max _{x_{1} \in \mathbb{R}}\left|u_{n}\left(x_{1}, x_{2}\right)\right| \rightarrow+\infty, \quad \text { as } n \rightarrow \infty$$

  for any $x_{2} \neq 0$.

  comment

• Paper 2, Section II, C

  Partial Differential Equations | Part II, 2013

  State the Lax-Milgram lemma.

  Let $\mathbf{V}=\mathbf{V}\left(x_{1}, x_{2}, x_{3}\right)$ be a smooth vector field which is $2 \pi$-periodic in each coordinate $x_{j}$ for $j=1,2,3$. Write down the definition of a weak $H_{p e r}^{1}$ solution for the equation

  $$-\Delta u+\sum_{j} V_{j} \partial_{j} u+u=f$$

  to be solved for $u=u\left(x_{1}, x_{2}, x_{3}\right)$ given $f=f\left(x_{1}, x_{2}, x_{3}\right)$ in $H^{0}$, with both $u$ and $f$ also $2 \pi$-periodic in each co-ordinate. [In this question use the definition

  $$H_{p e r}^{s}=\left\{u=\sum_{m \in \mathbb{Z}^{3}} \hat{u}(m) e^{i m \cdot x} \in L^{2}:\|u\|_{H^{s}}^{2}=\sum_{m \in \mathbb{Z}^{3}}\left(1+\|m\|^{2}\right)^{s}|\hat{u}(m)|^{2}<\infty\right\}$$

  for the Sobolev spaces of functions $2 \pi$-periodic in each coordinate $x_{j}$ and for $\left.s=0,1,2, \ldots\right]$

  If the vector field is divergence-free, prove that there exists a unique weak $H_{p e r}^{1}$ solution for all such $f$.

  Supposing that $\mathbf{V}$ is the constant vector field with components $(1,0,0)$, write down the solution of $(*)$ in terms of Fourier series and show that there exists $C>0$ such that

  $$\|u\|_{H^{2}} \leqslant C\|f\|_{H^{0}}$$

  comment

• Paper 3, Section II, C

  Partial Differential Equations | Part II, 2013

  Define the parabolic boundary $\partial_{p a r} \Omega_{T}$ of the domain $\Omega_{T}=[0,1] \times(0, T]$ for $T>0$.

  Let $u=u(x, t)$ be a smooth real-valued function on $\Omega_{T}$ which satisfies the inequality

  $$u_{t}-a u_{x x}+b u_{x}+c u \leqslant 0$$

  Assume that the coefficients $a, b$ and $c$ are smooth functions and that there exist positive constants $m, M$ such that $m \leqslant a \leqslant M$ everywhere, and $c \geqslant 0$. Prove that

  $$\max _{(x, t) \in \bar{\Omega}_{T}} u(x, t) \leqslant \max _{(x, t) \in \partial_{\text {par }} \Omega_{T}} u^{+}(x, t) .$$

  [Here $u^{+}=\max \{u, 0\}$ is the positive part of the function $u$.]

  Consider a smooth real-valued function $\phi$ on $\Omega_{T}$ such that

  $$\phi_{t}-\phi_{x x}-\left(1-\phi^{2}\right) \phi=0, \quad \phi(x, 0)=f(x)$$

  everywhere, and $\phi(0, t)=1=\phi(1, t)$ for all $t \geqslant 0$. Deduce from $(*)$ that if $f(x) \leqslant 1$ for all $x \in[0,1]$ then $\phi(x, t) \leqslant 1$ for all $(x, t) \in \Omega_{T}$. [Hint: Consider $u=\phi^{2}-1$ and compute $\left.u_{t}-u_{x x} \cdot\right]$

  comment

• Paper 4, Section II, C

  Partial Differential Equations | Part II, 2013

  (i) Show that an arbitrary $C^{2}$ solution of the one-dimensional wave equation $u_{t t}-u_{x x}=0$ can be written in the form $u=F(x-t)+G(x+t)$.

  Hence, deduce the formula for the solution at arbitrary $t>0$ of the Cauchy problem

  $$u_{t t}-u_{x x}=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x)$$

  where $u_{0}, u_{1}$ are arbitrary Schwartz functions.

  Deduce from this formula a theorem on finite propagation speed for the onedimensional wave equation.

  (ii) Define the Fourier transform of a tempered distribution. Compute the Fourier transform of the tempered distribution $T_{t} \in \mathcal{S}^{\prime}(\mathbb{R})$ defined for all $t>0$ by the function

  $$T_{t}(y)= \begin{cases}\frac{1}{2} & \text { if }|y| \leqslant t \\ 0 & \text { if }|y|>t\end{cases}$$

  that is, $\left\langle T_{t}, f\right\rangle=\frac{1}{2} \int_{-t}^{+t} f(y) d y$ for all $f \in \mathcal{S}(\mathbb{R})$. By considering the Fourier transform in $x$, deduce from this the formula for the solution of $(*)$ that you obtained in part (i) in the case $u_{0}=0$.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, E

  Principles of Quantum Mechanics | Part II, 2013

  Consider a composite system of several identical particles. Describe how the multiparticle state is constructed from single-particle states. For the case of two identical particles, describe how considering the interchange symmetry leads to the definition of bosons and fermions.

  Consider two non-interacting, identical particles, each with spin 1 . The singleparticle, spin-independent Hamiltonian $H\left(\hat{\mathbf{x}}_{i}, \hat{\mathbf{p}}_{i}\right)$ has non-degenerate eigenvalues $E_{n}$ and wavefunctions $\psi_{n}\left(\mathbf{x}_{i}\right)$ where $i=1,2$ labels the particle and $n=0,1,2,3, \ldots$ In terms of these single-particle wavefunctions and single-particle spin states $|1\rangle,|0\rangle$ and $|-1\rangle$, write down all of the two-particle states and energies for:

  (i) the ground state;

  (ii) the first excited state.

  Assume now that $E_{n}$ is a linear function of $n$. Find the degeneracy of the $N^{\text {th }}$energy level of the two-particle system for:

  (iii) $N$ even;

  (iv) $N$ odd.

  comment

• Paper 2, Section II, 33E

  Principles of Quantum Mechanics | Part II, 2013

  (i) In units where $\hbar=1$, angular momentum states $|j m\rangle$ obey

  $$J^{2}|j m\rangle=j(j+1)|j m\rangle, \quad J_{3}|j m\rangle=m|j m\rangle$$

  Use the algebra of angular momentum $\left[J_{i}, J_{j}\right]=i \epsilon_{i j k} J_{k}$ to derive the following in terms of $J^{2}, J_{\pm}=J_{1} \pm i J_{2}$ and $J_{3}$ : (a) $\left[J^{2}, J_{i}\right]$; (b) $\left[J_{3}, J_{\pm}\right]$; (c) $\left[J^{2}, J_{\pm}\right]$.

  (ii) Find $J_{+} J_{-}$in terms of $J^{2}$ and $J_{3}$. Thus calculate the quantum numbers of the state $J_{\pm}|j m\rangle$ in terms of $j$ and $m$. Derive the normalisation of the state $J_{-}|j m\rangle$. Therefore, show that

  $$\left\langle j j-1\left|J_{+}^{j-1} J_{-}^{j}\right| j j\right\rangle=\sqrt{A}(2 j-1) !$$

  finding $A$ in terms of $j$.

  (iii) Consider the combination of a spinless particle with an electron of spin $1 / 2$ and orbital angular momentum 1. Calculate the probability that the electron has a spin of $+1 / 2$ in the $z$-direction if the combined system has an angular momentum of $+1 / 2$ in the $z$-direction and a total angular momentum of $+3 / 2$. Repeat the calculation for a total angular momentum of $+1 / 2$.

  comment

• Paper 3, Section II, E

  Principles of Quantum Mechanics | Part II, 2013

  A particle moves in one dimension in an infinite square-well potential $V(x)=0$ for $|x|<a$ and $\infty$ for $|x|>a$. Find the energy eigenstates. Show that the energy eigenvalues are given by $E_{n}=E_{1} n^{2}$ for integer $n$, where $E_{1}$ is a constant which you should find.

  The system is perturbed by the potential $\delta V=\epsilon x / a$. Show that the energy of the $n^{\text {th }}$level $E_{n}$ remains unchanged to first order in $\epsilon$. Show that the ground-state wavefunction is

  $$\psi_{1}(x)=\frac{1}{\sqrt{a}}\left[\cos \frac{\pi x}{2 a}+\frac{D \epsilon}{\pi^{2} E_{1}} \sum_{n=2,4, \ldots}(-1)^{A n} \frac{n^{B}}{\left(n^{2}-1\right)^{C}} \sin \frac{n \pi x}{2 a}+\mathcal{O}\left(\epsilon^{2}\right)\right]$$

  where $A, B, C$ and $D$ are numerical constants which you should find. Briefly comment on the conservation of parity in the unperturbed and perturbed systems.

  comment

• Paper 4, Section II, E

  Principles of Quantum Mechanics | Part II, 2013

  (i) The creation and annihilation operators for a harmonic oscillator of angular frequency $\omega$ satisfy the commutation relation $\left[a, a^{\dagger}\right]=1$. Write down an expression for the Hamiltonian $H$ and number operator $N$ in terms of $a$ and $a^{\dagger}$. Explain how the space of eigenstates $|n\rangle, n=0,1,2, \ldots$, of $H$ is formed, and deduce the eigenenergies for these states. Show that

  $$a|n\rangle=\sqrt{n}|n-1\rangle, \quad a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle$$

  (ii) The operator $K_{r}$ is defined to be

  $$K_{r}=\frac{\left(a^{\dagger}\right)^{r} a^{r}}{r !}$$

  for $r=0,1,2, \ldots$ Show that $K_{r}$ commutes with $N$. Show that if $r \leqslant n$, then

  $$K_{r}|n\rangle=\frac{n !}{(n-r) ! r !}|n\rangle,$$

  and $K_{r}|n\rangle=0$ otherwise. By considering the action of $K_{r}$ on the state $|n\rangle$, deduce that

  $$\sum_{r=0}^{\infty}(-1)^{r} K_{r}=|0\rangle\langle 0|$$

  comment

Principles of Statistics

• Paper 1, Section II, K

  Principles of Statistics | Part II, 2013

  When the real parameter $\Theta$ takes value $\theta$, variables $X_{1}, X_{2}, \ldots$ arise independently from a distribution $P_{\theta}$ having density function $p_{\theta}(x)$ with respect to an underlying measure $\mu$. Define the score variable $U_{n}(\theta)$ and the information function $I_{n}(\theta)$ for estimation of $\Theta$ based on $\boldsymbol{X}^{n}:=\left(X_{1}, \ldots, X_{n}\right)$, and relate $I_{n}(\theta)$ to $i(\theta):=I_{1}(\theta)$.

  State and prove the Cramér-Rao inequality for the variance of an unbiased estimator of $\Theta$. Under what conditions does this inequality become an equality? What is the form of the estimator in this case? [You may assume $\mathbb{E}_{\theta}\left\{U_{n}(\theta)\right\}=0, \operatorname{var}_{\theta}\left\{U_{n}(\theta)\right\}=I_{n}(\theta)$, and any further required regularity conditions, without comment.]

  Let $\widehat{\Theta}_{n}$ be the maximum likelihood estimator of $\Theta$ based on $\boldsymbol{X}^{n}$. What is the asymptotic distribution of $n^{\frac{1}{2}}\left(\widehat{\Theta}_{n}-\Theta\right)$ when $\Theta=\theta$ ?

  Suppose that, for each $n, \widehat{\Theta}_{n}$ is unbiased for $\Theta$, and the variance of $n^{\frac{1}{2}}\left(\widehat{\Theta}_{n}-\Theta\right)$ is exactly equal to its asymptotic variance. By considering the estimator $\alpha \widehat{\Theta}_{k}+(1-\alpha) \widehat{\Theta}_{n}$, or otherwise, show that, for $k<n, \operatorname{cov}_{\theta}\left(\widehat{\Theta}_{k}, \widehat{\Theta}_{n}\right)=\operatorname{var}_{\theta}\left(\widehat{\Theta}_{n}\right)$.

  comment

• Paper 2, Section II, K

  Principles of Statistics | Part II, 2013

  Describe the Weak Sufficiency Principle (WSP) and the Strong Sufficiency Principle (SSP). Show that Bayesian inference with a fixed prior distribution respects WSP.

  A parameter $\Phi$ has a prior distribution which is normal with mean 0 and precision (inverse variance) $h_{\Phi} .$ Given $\Phi=\phi$, further parameters $\Theta:=\left(\Theta{ }_{i}: i=1, \ldots, I\right)$ have independent normal distributions with mean $\phi$ and precision $h_{\Theta}$. Finally, given both $\Phi=\phi$ and $\boldsymbol{\Theta}=\boldsymbol{\theta}:=\left(\theta_{1}, \ldots, \theta_{I}\right)$, observables $\boldsymbol{X}:=\left(X_{i j}: i=1, \ldots, I ; j=1, \ldots, J\right)$ are independent, $X_{i j}$ being normal with mean $\theta_{i}$, and precision $h_{X}$. The precision parameters $\left(h_{\Phi}, h_{\Theta}, h_{X}\right)$ are all fixed and known. Let $\overline{\boldsymbol{X}}:=\left(\bar{X}_{1}, \ldots, \bar{X}_{I}\right)$, where $\bar{X}_{i}:=\sum_{j=1}^{J} X_{i j} / J$. Show, directly from the definition of sufficiency, that $\overline{\boldsymbol{X}}$ is sufficient for $(\Phi, \Theta)$. [You may assume without proof that, if $Y_{1}, \ldots, Y_{n}$ have independent normal distributions with the same variance, and $\bar{Y}:=n^{-1} \sum_{i=1}^{n} Y_{i}$, then the vector $\left(Y_{1}-\bar{Y}, \ldots, Y_{n}-\bar{Y}\right)$ is independent of $\bar{Y}$.]

  For data-values $\boldsymbol{x}:=\left(x_{i j}: i=1, \ldots, I ; j=1, \ldots, J\right)$, determine the joint distribution, $\Pi_{\phi}$ say, of $\Theta$, given $\boldsymbol{X}=\boldsymbol{x}$ and $\Phi=\phi .$ What is the distribution of $\Phi$, given $\boldsymbol{\Theta}=\boldsymbol{\theta}$ and $\boldsymbol{X}=\boldsymbol{x} ?$

  Using these results, describe clearly how Gibbs sampling combined with RaoBlackwellisation could be applied to estimate the posterior joint distribution of $\Theta$, given $\boldsymbol{X}=\boldsymbol{x}$.

  comment

• Paper 3, Section II, K

  Principles of Statistics | Part II, 2013

  What is meant by a convex decision problem? State and prove a theorem to the effect that, in a convex decision problem, there is no point in randomising. [You may use standard terms without defining them.]

  The sample space, parameter space and action space are each the two-point set $\{1,2\}$. The observable $X$ takes value 1 with probability $2 / 3$ when the parameter $\Theta=1$, and with probability $3 / 4$ when $\Theta=2$. The loss function $L(\theta, a)$ is 0 if $a=\theta$, otherwise 1 . Describe all the non-randomised decision rules, compute their risk functions, and plot these as points in the unit square. Identify an inadmissible non-randomised decision rule, and a decision rule that dominates it.

  Show that the minimax rule has risk function $(8 / 17,8 / 17)$, and is Bayes against a prior distribution that you should specify. What is its Bayes risk? Would a Bayesian with this prior distribution be bound to use the minimax rule?

  comment

• Paper 4, Section II, $27 \mathrm{~K}$

  Principles of Statistics | Part II, 2013

  Assuming only the existence and properties of the univariate normal distribution, define $\mathcal{N}_{p}(\underline{\mu}, \Sigma)$, the multivariate normal distribution with mean (row-)vector $\underline{\mu}$ and dispersion matrix $\Sigma$; and $W_{p}(\nu ; \Sigma)$, the Wishart distribution on integer $\nu>1$ degrees of freedom and with scale parameter $\Sigma$. Show that, if $\underline{X} \sim \mathcal{N}_{p}(\underline{\mu}, \Sigma), S \sim W_{p}(\nu ; \Sigma)$, and $\underline{b}(1 \times q), A(p \times q)$ are fixed, then $\underline{b}+\underline{X} A \sim \mathcal{N}_{q}(\underline{b}+\underline{\mu} A, \Phi), A^{\mathrm{T}} S A \sim W_{p}(\nu ; \Phi)$, where $\Phi=A^{\mathrm{T}} \Sigma A$.

  The random $(n \times p)$ matrix $X$ has rows that are independently distributed as $\mathcal{N}_{p}(\underline{\mathrm{M}}, \Sigma)$, where both parameters $\underline{\mathrm{M}}$ and $\Sigma$ are unknown. Let $\underline{\bar{X}}:=n^{-1} \mathbf{1}^{\mathrm{T}} X$, where 1 is the $(n \times 1)$ vector of $1 \mathrm{~s}$; and $S^{c}:=X^{\mathrm{T}} \Pi X$, with $\Pi:=I_{n}-n^{-1} 11^{\mathrm{T}}$. State the joint distribution of $\bar{X}$ and $S^{c}$ given the parameters.

  Now suppose $n>p$ and $\Sigma$ is positive definite. Hotelling's $T^{2}$ is defined as

  $$T^{2}:=n(\underline{\bar{X}}-\underline{\mathrm{M}})\left(\bar{S}^{c}\right)^{-1}(\underline{\bar{X}}-\underline{\mathrm{M}})^{\mathrm{T}}$$

  where $\bar{S}^{c}:=S^{c} / \nu$ with $\nu:=(n-1)$. Show that, for any values of $\underline{\mathrm{M}}$ and $\Sigma$,

  $$\left(\frac{\nu-p+1}{\nu p}\right) T^{2} \sim F_{\nu-p+1}^{p},$$

  the $F$ distribution on $p$ and $\nu-p+1$ degrees of freedom.

  [You may assume that:

  1. If $S \sim W_{p}(\nu ; \Sigma)$ and $\mathbf{a}$ is a fixed $(p \times 1)$ vector, then

  $$\frac{\mathbf{a}^{\mathrm{T}} \Sigma^{-1} \mathbf{a}}{\mathbf{a}^{\mathrm{T}} S^{-1} \mathbf{a}} \sim \chi_{\nu-p+1}^{2}$$

  2. If $V \sim \chi_{p}^{2}, W \sim \chi_{\lambda}^{2}$ are independent, then

  $$\frac{V / p}{W / \lambda} \sim F_{\lambda}^{p} \text {. }$$

  comment

Probability and Measure

• Paper 1, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2013

  State Dynkin's $\pi$-system $/ d$-system lemma.

  Let $\mu$ and $\nu$ be probability measures on a measurable space $(E, \mathcal{E})$. Let $\mathcal{A}$ be a $\pi$-system on $E$ generating $\mathcal{E}$. Suppose that $\mu(A)=\nu(A)$ for all $A \in \mathcal{A}$. Show that $\mu=\nu$.

  What does it mean to say that a sequence of random variables is independent?

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables, all uniformly distributed on $[0,1]$. Let $Y$ be another random variable, independent of $\left(X_{n}: n \in \mathbb{N}\right)$. Define random variables $Z_{n}$ in $[0,1]$ by $Z_{n}=\left(X_{n}+Y\right) \bmod 1$. What is the distribution of $Z_{1}$ ? Justify your answer.

  Show that the sequence of random variables $\left(Z_{n}: n \in \mathbb{N}\right)$ is independent.

  comment

• Paper 2, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2013

  Let $\left(f_{n}: n \in \mathbb{N}\right)$ be a sequence of non-negative measurable functions defined on a measure space $(E, \mathcal{E}, \mu)$. Show that $\liminf _{n} f_{n}$ is also a non-negative measurable function.

  State the Monotone Convergence Theorem.

  State and prove Fatou's Lemma.

  Let $\left(f_{n}: n \in \mathbb{N}\right)$ be as above. Suppose that $f_{n}(x) \rightarrow f(x)$ as $n \rightarrow \infty$ for all $x \in E$. Show that

  $$\mu\left(\min \left\{f_{n}, f\right\}\right) \rightarrow \mu(f) .$$

  Deduce that, if $f$ is integrable and $\mu\left(f_{n}\right) \rightarrow \mu(f)$, then $f_{n}$ converges to $f$ in $L^{1}$. [Still assume that $f_{n}$ and $f$ are as above.]

  comment

• Paper 3, Section II, $25 K$

  Probability and Measure | Part II, 2013

  Let $X$ be an integrable random variable with $\mathbb{E}(X)=0$. Show that the characteristic function $\phi_{X}$ is differentiable with $\phi_{X}^{\prime}(0)=0$. [You may use without proof standard convergence results for integrals provided you state them clearly.]

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables, all having the same distribution as $X$. Set $S_{n}=X_{1}+\cdots+X_{n}$. Show that $S_{n} / n \rightarrow 0$ in distribution. Deduce that $S_{n} / n \rightarrow 0$ in probability. [You may not use the Strong Law of Large Numbers.]

  comment

• Paper 4, Section II, K

  Probability and Measure | Part II, 2013

  State Birkhoff's almost-everywhere ergodic theorem.

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables such that

  $$\mathbb{P}\left(X_{n}=0\right)=\mathbb{P}\left(X_{n}=1\right)=1 / 2$$

  Define for $k \in \mathbb{N}$

  $$Y_{k}=\sum_{n=1}^{\infty} X_{k+n-1} / 2^{n}$$

  What is the distribution of $Y_{k} ? \quad$ Show that the random variables $Y_{1}$ and $Y_{2}$ are not independent.

  Set $S_{n}=Y_{1}+\cdots+Y_{n}$. Show that $S_{n} / n$ converges as $n \rightarrow \infty$ almost surely and determine the limit. [You may use without proof any standard theorem provided you state it clearly.]

  comment

Representation Theory

• Paper 1, Section II, 19G

  Representation Theory | Part II, 2013

  State and prove Maschke's Theorem for complex representations of finite groups.

  Without using character theory, show that every irreducible complex representation of the dihedral group of order $10, D_{10}$, has dimension at most two. List the irreducible complex representations of $D_{10}$ up to isomorphism.

  Let $V$ be the set of vertices of a regular pentagon with the usual action of $D_{10}$. Explicitly decompose the permutation representation $\mathbb{C} V$ into a direct sum of irreducible subrepresentations.

  comment

• Paper 2, Section II, G

  Representation Theory | Part II, 2013

  Recall that a regular icosahedron has 20 faces, 30 edges and 12 vertices. Let $G$ be the group of rotational symmetries of a regular icosahedron.

  Compute the conjugacy classes of $G$. Hence, or otherwise, construct the character table of $G$. Using the character table explain why $G$ must be a simple group.

  [You may use any general theorems provided that you state them clearly.]

  comment

• Paper 3, Section II, G

  Representation Theory | Part II, 2013

  Suppose that $\left(\rho_{1}, V_{1}\right)$ and $\left(\rho_{2}, V_{2}\right)$ are complex representations of the finite groups $G_{1}$ and $G_{2}$ respectively. Use $\rho_{1}$ and $\rho_{2}$ to construct a representation $\rho_{1} \otimes \rho_{2}$ of $G_{1} \times G_{2}$ on $V_{1} \otimes V_{2}$ and show that its character satisfies

  $$\chi \rho_{1} \otimes \rho_{2}\left(g_{1}, g_{2}\right)=\chi_{\rho_{1}}\left(g_{1}\right) \chi \rho_{2}\left(g_{2}\right)$$

  for each $g_{1} \in G_{1}, g_{2} \in G_{2}$.

  Prove that if $\rho_{1}$ and $\rho_{2}$ are irreducible then $\rho_{1} \otimes \rho_{2}$ is irreducible as a representation of $G_{1} \times G_{2}$. Moreover, show that every irreducible complex representation of $G_{1} \times G_{2}$ arises in this way.

  Is it true that every complex representation of $G_{1} \times G_{2}$ is of the form $\rho_{1} \otimes \rho_{2}$ with $\rho_{i}$ a complex representation of $G_{i}$ for $i=1,2 ?$ Justify your answer.

  comment

• Paper 4, Section II, G

  Representation Theory | Part II, 2013

  State and prove Burnside's $p^{a} q^{b}$-theorem.

  comment

Riemann Surfaces

• Paper 1, Section II, I

  Riemann Surfaces | Part II, 2013

  (i) Let $f(z)=\sum_{n=0}^{\infty} a_{n} z^{n}$ be a power series with radius of convergence $r$ in $(0, \infty)$. Show that there is at least one point $a$ on the circle $C=\{z \in \mathbb{C}:|z|=r\}$ which is a singular point of $f$, that is, there is no direct analytic continuation of $f$ in any neighbourhood of $a$.

  (ii) Let $X$ and $Y$ be connected Riemann surfaces. Define the space $\mathcal{G}$ of germs of function elements of $X$ into $Y$. Define the natural topology on $\mathcal{G}$ and the natural $\operatorname{map} \pi: \mathcal{G} \rightarrow X$. [You may assume without proof that the topology on $\mathcal{G}$ is Hausdorff.] Show that $\pi$ is continuous. Define the natural complex structure on $\mathcal{G}$ which makes it into a Riemann surface. Finally, show that there is a bijection between the connected components of $\mathcal{G}$ and the complete holomorphic functions of $X$ into $Y$.

  comment

• Paper 2, Section II, I

  Riemann Surfaces | Part II, 2013

  (i) Show that the open unit $\operatorname{disc} D=\{z \in \mathbb{C}:|z|<1\}$ is biholomorphic to the upper half-plane $\mathbb{H}=\{z \in \mathbb{C}: \operatorname{Im}(z)>0\}$.

  (ii) Define the degree of a non-constant holomorphic map between compact connected Riemann surfaces. State the Riemann-Hurwitz formula without proof. Now let $X$ be a complex torus and $f: X \rightarrow Y$ a holomorphic map of degree 2 , where $Y$ is the Riemann sphere. Show that $f$ has exactly four branch points.

  (iii) List without proof those Riemann surfaces whose universal cover is the Riemann sphere or $\mathbb{C}$. Now let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a holomorphic map such that there are two distinct elements $a, b \in \mathbb{C}$ outside the image of $f$. Assuming the uniformization theorem and the monodromy theorem, show that $f$ is constant.

  comment

• Paper 3, Section II, I

  Riemann Surfaces | Part II, 2013

  Let $\Lambda=\mathbb{Z}+\mathbb{Z} \lambda$ be a lattice in $\mathbb{C}$ where $\operatorname{Im}(\lambda)>0$, and let $X$ be the complex torus $\mathbb{C} / \Lambda .$

  (i) Give the definition of an elliptic function with respect to $\Lambda$. Show that there is a bijection between the set of elliptic functions with respect to $\Lambda$ and the set of holomorphic maps from $X$ to the Riemann sphere. Next, show that if $f$ is an elliptic function with respect to $\Lambda$ and $f^{-1}\{\infty\}=\emptyset$, then $f$ is constant.

  (ii) Assume that

  $$f(z)=\frac{1}{z^{2}}+\sum_{\omega \in \Lambda \backslash\{0\}}\left(\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}}\right)$$

  defines a meromorphic function on $\mathbb{C}$, where the sum converges uniformly on compact subsets of $\mathbb{C} \backslash \Lambda$. Show that $f$ is an elliptic function with respect to $\Lambda$. Calculate the order of $f$.

  Let $g$ be an elliptic function with respect to $\Lambda$ on $\mathbb{C}$, which is holomorphic on $\mathbb{C} \backslash \Lambda$ and whose only zeroes in the closed parallelogram with vertices $\{0,1, \lambda, \lambda+1\}$ are simple zeroes at the points $\left\{\frac{1}{2}, \frac{\lambda}{2}, \frac{1}{2}+\frac{\lambda}{2}\right\}$. Show that $g$ is a non-zero constant multiple of $f^{\prime}$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2013

  Variables $Y_{1}, \ldots, Y_{n}$ are independent, with $Y_{i}$ having a density $p\left(y \mid \mu_{i}\right)$ governed by an unknown parameter $\mu_{i}$. Define the deviance for a model $M$ that imposes relationships between the $\left(\mu_{i}\right)$.

  From this point on, suppose $Y_{i} \sim \operatorname{Poisson}\left(\mu_{i}\right)$. Write down the log-likelihood of data $y_{1}, \ldots, y_{n}$ as a function of $\mu_{1}, \ldots, \mu_{n}$.

  Let $\widehat{\mu}_{i}$ be the maximum likelihood estimate of $\mu_{i}$ under model $M$. Show that the deviance for this model is given by

  $$2 \sum_{i=1}^{n}\left\{y_{i} \log \frac{y_{i}}{\widehat{\mu}_{i}}-\left(y_{i}-\widehat{\mu}_{i}\right)\right\}$$

  Now suppose that, under $M, \log \mu_{i}=\beta^{\mathrm{T}} x_{i}, i=1, \ldots, n$, where $x_{1}, \ldots, x_{n}$ are known $p$-dimensional explanatory variables and $\beta$ is an unknown $p$-dimensional parameter. Show that $\widehat{\mu}:=\left(\widehat{\mu}_{1}, \ldots, \widehat{\mu}_{n}\right)^{\mathrm{T}}$ satisfies $X^{\mathrm{T}} y=X^{\mathrm{T}} \widehat{\mu}$, where $y=\left(y_{1}, \ldots, y_{n}\right)^{\mathrm{T}}$ and $X$ is the $(n \times p)$ matrix with rows $x_{1}^{\mathrm{T}}, \ldots, x_{n}^{\mathrm{T}}$, and express this as an equation for the maximum likelihood estimate $\widehat{\beta}$ of $\beta$. [You are not required to solve this equation.]

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2013

  A cricket ball manufacturing company conducts the following experiment. Every day, a bowling machine is set to one of three levels, "Medium", "Fast" or "Spin", and then bowls 100 balls towards the stumps. The number of times the ball hits the stumps and the average wind speed (in kilometres per hour) during the experiment are recorded, yielding the following data (abbreviated):

  $\begin{array}{llll}\text { Day } & \text { Wind } & \text { Level } & \text { Stumps } \\ 1 & 10 & \text { Medium } & 26 \\ 2 & 8 & \text { Medium } & 37 \\ \vdots & \vdots & \vdots & \vdots \\ 50 & 12 & \text { Medium } & 32 \\ 51 & 7 & \text { Fast } & 31 \\ \vdots & \vdots & \vdots & \vdots \\ 120 & 3 & \text { Fast } & 28 \\ 121 & 5 & \text { Spin } & 35 \\ \vdots & \vdots & \vdots & \vdots \\ 150 & 6 & \text { Spin } & 31\end{array}$

  Write down a reasonable model for $Y_{1}, \ldots, Y_{150}$, where $Y_{i}$ is the number of times the ball hits the stumps on the $i^{t h}$ day. Explain briefly why we might want to include interactions between the variables. Write $R$ code to fit your model.

  The company's statistician fitted her own generalized linear model using $\mathrm{R}$, and obtained the following summary (abbreviated):

  $\begin{array}{lrrrrr}\text { >summary(ball) } & & & & \\ \text { Coefficients: } & & & & & \\ & \text { Estimate } & \text { Std. Error } & \text { z value } & \operatorname{Pr}(>|z|) & \\ \text { (Intercept) } & -0.37258 & 0.05388 & -6.916 & 4.66 \mathrm{e}-12 & * * * \\ \text { Wind } & 0.09055 & 0.01595 & 5.676 & 1.38 \mathrm{e}-08 & * * * \\ \text { LevelFast } & -0.10005 & 0.08044 & -1.244 & 0.213570 & \\ \text { LevelSpin } & 0.29881 & 0.08268 & 3.614 & 0.000301 & * * * \\ \text { Wind: LevelFast } & 0.03666 & 0.02364 & 1.551 & 0.120933 & \\ \text { Wind: LevelSpin } & -0.07697 & 0.02845 & -2.705 & 0.006825 & * *\end{array}$

  Why are LevelMedium and Wind: LevelMedium not listed?

  Suppose that, on another day, the bowling machine is set to "Spin", and the wind speed is 5 kilometres per hour. What linear function of the parameters should the statistician use in constructing a predictor of the number of times the ball hits the stumps that day?

  Based on the above output, how might you improve the model? How could you fit your new model in $R$ ?

  comment

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2013

  Consider a linear model $Y=X \beta+\epsilon$, where $Y$ and $\epsilon$ are $(n \times 1)$ with $\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$, $\beta$ is $(p \times 1)$, and $X$ is $(n \times p)$ of full $\operatorname{rank} p<n$. Let $\gamma$ and $\delta$ be sub-vectors of $\beta$. What is meant by orthogonality between $\gamma$ and $\delta$ ?

  Now suppose

  $$Y_{i}=\beta_{0}+\beta_{1} x_{i}+\beta_{2} x_{i}^{2}+\beta_{3} P_{3}\left(x_{i}\right)+\epsilon_{i} \quad(i=1, \ldots, n),$$

  where $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent $N\left(0, \sigma^{2}\right)$ random variables, $x_{1}, \ldots, x_{n}$ are real-valued known explanatory variables, and $P_{3}(x)$ is a cubic polynomial chosen so that $\beta_{3}$ is orthogonal to $\left(\beta_{0}, \beta_{1}, \beta_{2}\right)^{\mathrm{T}}$ and $\beta_{1}$ is orthogonal to $\left(\beta_{0}, \beta_{2}\right)^{\mathrm{T}}$.

  Let $\widetilde{\beta}=\left(\beta_{0}, \beta_{2}, \beta_{1}, \beta_{3}\right)^{\mathrm{T}}$. Describe the matrix $\widetilde{X}$such that $Y=\widetilde{X} \widetilde{\beta}+\epsilon$. Show that $\widetilde{X}^{\mathrm{T}} \widetilde{X}$is block diagonal. Assuming further that this matrix is non-singular, show that the least-squares estimators of $\beta_{1}$ and $\beta_{3}$ are, respectively,

  $$\widehat{\beta}_{1}=\frac{\sum_{i=1}^{n} x_{i} Y_{i}}{\sum_{i=1}^{n} x_{i}^{2}} \quad \text { and } \quad \widehat{\beta}_{3}=\frac{\sum_{i=1}^{n} P_{3}\left(x_{i}\right) Y_{i}}{\sum_{i=1}^{n} P_{3}\left(x_{i}\right)^{2}}$$

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2013

  Consider the linear model $Y=X \beta+\epsilon$ where $Y=\left(Y_{1}, \ldots, Y_{n}\right)^{\mathrm{T}}, \beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{\mathrm{T}}$, and $\epsilon=\left(\epsilon_{1}, \ldots, \epsilon_{n}\right)^{\mathrm{T}}$, with $\epsilon_{1}, \ldots, \epsilon_{n}$ independent $N\left(0, \sigma^{2}\right)$ random variables. The $(n \times p)$ matrix $X$ is known and is of full rank $p<n$. Give expressions for the maximum likelihood estimators $\widehat{\beta}$ and $\widehat{\sigma}^{2}$ of $\beta$ and $\sigma^{2}$ respectively, and state their joint distribution. Show that $\widehat{\beta}$ is unbiased whereas $\widehat{\sigma}^{2}$ is biased.

  Suppose that a new variable $Y^{*}$ is to be observed, satisfying the relationship

  $$Y^{*}=x^{* \mathrm{~T}} \beta+\epsilon^{*}$$

  where $x^{*}(p \times 1)$ is known, and $\epsilon^{*} \sim N\left(0, \sigma^{2}\right)$ independently of $\epsilon$. We propose to predict $Y^{*}$ by $\widetilde{Y}=x^{* \mathrm{~T}} \widehat{\beta}$. Identify the distribution of

  $$\frac{Y^{*}-\tilde{Y}}{\tau \tilde{\sigma}}$$

  where

  $$\begin{aligned} \tilde{\sigma}^{2} &=\frac{n}{n-p} \widehat{\sigma}^{2} \\ \tau^{2} &=x^{* \mathrm{~T}}\left(X^{\mathrm{T}} X\right)^{-1} x^{*}+1 \end{aligned}$$

  comment

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2013

  The output $X$ of a process depends on the levels of two adjustable variables: $A$, a factor with four levels, and $B$, a factor with two levels. For each combination of a level of $A$ and a level of $B$, nine independent values of $X$ are observed.

  Explain and interpret the $R$ commands and (abbreviated) output below. In particular, describe the model being fitted, and describe and comment on the hypothesis tests performed under the summary and anova commands.

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2013

  Let $f_{0}$ be a probability density function, with cumulant generating function $K$. Define what it means for a random variable $Y$ to have a model function of exponential dispersion family form, generated by $f_{0}$.

  A random variable $Y$ is said to have an inverse Gaussian distribution, with parameters $\phi$ and $\lambda$ (both positive), if its density function is

  $$f(y ; \phi, \lambda)=\frac{\sqrt{\lambda}}{\sqrt{2 \pi y^{3}}} e^{\sqrt{\lambda \phi}} \exp \left\{-\frac{1}{2}\left(\frac{\lambda}{y}+\phi y\right)\right\} \quad(y>0)$$

  Show that the family of all inverse Gaussian distributions for $Y$ is of exponential dispersion family form. Deduce directly the corresponding expressions for $E(Y)$ and $\operatorname{Var}(Y)$ in terms of $\phi$ and $\lambda$. What are the corresponding canonical link function and variance function?

  Consider a generalized linear model, $M$, for independent variables $Y_{i}(i=1, \ldots, n)$, whose random component is defined by the inverse Gaussian distribution with link function $g(\mu)=\log (\mu):$ thus $g\left(\mu_{i}\right)=x_{i}^{\mathrm{T}} \beta$, where $\beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{\mathrm{T}}$ is the vector of unknown regression coefficients and $x_{i}=\left(x_{i 1}, \ldots, x_{i p}\right)^{\mathrm{T}}$ is the vector of known values of the explanatory variables for the $i^{\text {th }}$observation. The vectors $x_{i}(i=1, \ldots, n)$ are linearly independent. Assuming that the dispersion parameter is known, obtain expressions for the score function and Fisher information matrix for $\beta$. Explain how these can be used to compute the maximum likelihood estimate $\widehat{\beta}$ of $\beta$.

  comment

Statistical Physics

• Paper 1, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) What is the occupation number of a state $i$ with energy $E_{i}$ according to the Fermi-Dirac statistics for a given chemical potential $\mu$ ?

  (ii) Assuming that the energy $E$ is spin independent, what is the number $g_{s}$ of electrons which can occupy an energy level?

  (iii) Consider a semi-infinite metal slab occupying $z \leqslant 0$ (and idealized to have infinite extent in the $x y$ plane) and a vacuum environment at $z>0$. An electron with momentum $\left(p_{x}, p_{y}, p_{z}\right)$ inside the slab will escape the metal in the $+z$ direction if it has a sufficiently large momentum $p_{z}$ to overcome a potential barrier $V_{0}$ relative to the Fermi energy $\epsilon_{\mathrm{F}}$, i.e. if

  $$\frac{p_{z}^{2}}{2 m} \geqslant \epsilon_{\mathrm{F}}+V_{0}$$

  where $m$ is the electron mass.

  At fixed temperature $T$, some fraction of electrons will satisfy this condition, which results in a current density $j_{z}$ in the $+z$ direction (an electron having escaped the metal once is considered lost, never to return). Each electron escaping provides a contribution $\delta j_{z}=-e v_{z}$ to this current density, where $v_{z}$ is the velocity and $e$ the elementary charge.

  (a) Briefly describe the Fermi-Dirac distribution as a function of energy in the limit $k_{\mathrm{B}} T \ll \epsilon_{\mathrm{F}}$, where $k_{\mathrm{B}}$ is the Boltzmann constant. What is the chemical potential $\mu$ in this limit?

  (b) Assume that the electrons behave like an ideal, non-relativistic Fermi gas and that $k_{\mathrm{B}} T \ll V_{0}$ and $k_{\mathrm{B}} T \ll \epsilon_{\mathrm{F}}$. Calculate the current density $j_{z}$ associated with the electrons escaping the metal in the $+z$ direction. How could we easily increase the strength of the current?

  comment

• Paper 2, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) The first law of thermodynamics is $d E=T d S-p d V+\mu d N$, where $\mu$ is the chemical potential. Briefly describe its meaning.

  (ii) What is equipartition of energy? Under which conditions is it valid? Write down the heat capacity $C_{V}$ at constant volume for a monatomic ideal gas.

  (iii) Starting from the first law of thermodynamics, and using the fact that for an ideal gas $(\partial E / \partial V)_{T}=0$, show that the entropy of an ideal gas containing $N$ particles can be written as

  $$S(T, V)=N\left(\int \frac{c_{V}(T)}{T} d T+k_{\mathrm{B}} \ln \frac{V}{N}+\mathrm{const}\right)$$

  where $T$ and $V$ are temperature and volume of the gas, $k_{\mathrm{B}}$ is the Boltzmann constant, and we define the heat capacity per particle as $c_{V}=C_{V} / N$.

  (iv) The Gibbs free energy $G$ is defined as $G=E+p V-T S$. Verify that it is a function of temperature $T$, pressure $p$ and particle number $N$. Explain why $G$ depends on the particle number $N$ through $G=\mu(T, p) N$.

  (v) Calculate the chemical potential $\mu$ for an ideal gas with heat capacity per particle $c_{V}(T)$. Calculate $\mu$ for the special case of a monatomic gas.

  comment

• Paper 3, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) Briefly describe the microcanonical ensemble.

  (ii) For quantum mechanical systems the energy levels are discrete. Explain why we can write the probability distribution in this case as

  $$p\left(\left\{n_{i}\right\}\right)= \begin{cases}\text { const }>0 & \text { for } E \leqslant E\left(\left\{n_{i}\right\}\right)<E+\Delta E \\ 0 & \text { otherwise }\end{cases}$$

  What assumption do we make for the energy interval $\Delta E$ ?

  Consider $N$ independent linear harmonic oscillators of equal frequency $\omega$. Their total energy is given by

  $$E\left(\left\{n_{i}\right\}\right)=\sum_{i=1}^{N} \hbar \omega\left(n_{i}+\frac{1}{2}\right)=M \hbar \omega+\frac{N}{2} \hbar \omega \quad \text { with } \quad M=\sum_{i=1}^{N} n_{i}$$

  Here $n_{i}=0,1,2, \ldots$ is the excitation number of oscillator $i$.

  (iii) Show that, for fixed $N$ and $M$, the number $g_{N}(M)$ of possibilities to distribute the $M$ excitations over $N$ oscillators (i.e. the number of different choices $\left\{n_{i}\right\}$ consistent with $M$ ) is given by

  $$g_{N}(M)=\frac{(M+N-1) !}{M !(N-1) !}$$

  [Hint: You may wish to consider the set of $N$ oscillators plus $M-1$ "additional" excitations and what it means to choose $M$ objects from this set.]

  (iv) Using the probability distribution of part (ii), calculate the probability distribution $p\left(E_{1}\right)$ for the "first" oscillator as a function of its energy $E_{1}=n_{1} \hbar \omega+\frac{1}{2} \hbar \omega$.

  (v) If $\Delta E=\hbar \omega \ll E$ then exactly one value of $M$ will correspond to a total energy inside the interval $(E, E+\Delta E)$. In this case, show that

  $$p\left(E_{1}\right) \approx \frac{g_{N-1}\left(M-n_{1}\right)}{g_{N}(M)} .$$

  Approximate this result in the limit $N \gg 1, M \gg n_{1}$.

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2013

  A classical particle of mass $m$ moving non-relativistically in two-dimensional space is enclosed inside a circle of radius $R$ and attached by a spring with constant $\kappa$ to the centre of the circle. The particle thus moves in a potential

  $$V(r)= \begin{cases}\frac{1}{2} \kappa r^{2} & \text { for } r<R \\ \infty & \text { for } r \geqslant R\end{cases}$$

  where $r^{2}=x^{2}+y^{2}$. Let the particle be coupled to a heat reservoir at temperature $T$.

  (i) Which of the ensembles of statistical physics should be used to model the system?

  (ii) Calculate the partition function for the particle.

  (iii) Calculate the average energy $\langle E\rangle$ and the average potential energy $\langle V\rangle$ of the particle.

  (iv) What is the average energy in:

  (a) the limit $\frac{1}{2} \kappa R^{2} \gg k_{\mathrm{B}} T$ (strong coupling)?

  (b) the limit $\frac{1}{2} \kappa R^{2} \ll k_{\mathrm{B}} T$ (weak coupling)?

  Compare the two results with the values expected from equipartition of energy.

  comment

Stochastic Financial Models

• Paper 1, Section II, 29J

  Stochastic Financial Models | Part II, 2013

  (i) Suppose that the price $S_{t}$ of an asset at time $t$ is given by

  $$S_{t}=S_{0} \exp \left\{\sigma B_{t}+\left(r-\frac{1}{2} \sigma^{2}\right) t\right\}$$

  where $B$ is a Brownian motion, $S_{0}$ and $\sigma$ are positive constants, and $r$ is the riskless rate of interest, assumed constant. In this model, explain briefly why the time-0 price of a derivative which delivers a bounded random variable $Y$ at time $T$ should be given by $E\left(e^{-r T} Y\right)$. What feature of this model ensures that the price is unique?

  Derive an expression $C\left(S_{0}, K, T, r, \sigma\right)$ for the time- 0 price of a European call option with strike $K$ and expiry $T$. Explain the italicized terms.

  (ii) Suppose now that the price $X_{t}$ of an asset at time $t$ is given by

  $$X_{t}=\sum_{j=1}^{n} w_{j} \exp \left\{\sigma_{j} B_{t}+\left(r-\frac{1}{2} \sigma_{j}^{2}\right) t\right\}$$

  where the $w_{j}$ and $\sigma_{j}$ are positive constants, and the other notation is as in part (i) above. Show that the time-0 price of a European call option with strike $K$ and expiry $T$ written on this asset can be expressed as

  $$\sum_{j=1}^{n} C\left(w_{j}, k_{j}, T, r, \sigma_{j}\right)$$

  where the $k_{j}$ are constants. Explain how the $k_{j}$ are characterized.

  comment

• Paper 2, Section II, J

  Stochastic Financial Models | Part II, 2013

  What does it mean to say that $\left(Y_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a supermartingale?

  State and prove Doob's Upcrossing Inequality for a supermartingale.

  Let $\left(M_{n}, \mathcal{F}_{n}\right)_{n \leqslant 0}$ be a martingale indexed by negative time, that is, for each $n \leqslant 0$, $\mathcal{F}_{n-1} \subseteq \mathcal{F}_{n}, M_{n} \in L^{1}\left(\mathcal{F}_{n}\right)$ and $E\left[M_{n} \mid \mathcal{F}_{n-1}\right]=M_{n-1}$. Using Doob's Upcrossing Inequality, prove that the limit $\lim _{n \rightarrow-\infty} M_{n}$ exists almost surely.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models | Part II, 2013

  Suppose that $\left(\varepsilon_{t}\right)_{t=0,1, \ldots, T}$ is a sequence of independent and identically distributed random variables such that $E \exp \left(z \varepsilon_{1}\right)<\infty$ for all $z \in \mathbb{R}$. Each day, an agent receives an income, the income on day $t$ being $\varepsilon_{t}$. After receiving this income, his wealth is $w_{t}$. From this wealth, he chooses to consume $c_{t}$, and invests the remainder $w_{t}-c_{t}$ in a bank account which pays a daily interest rate of $r>0$. Write down the equation for the evolution of $w_{t}$.

  Suppose we are given constants $\beta \in(0,1), A_{T}, \gamma>0$, and define the functions

  $$U(x)=-\exp (-\gamma x), \quad U_{T}(x)=-A_{T} \exp (-\nu x)$$

  where $\nu:=\gamma r /(1+r)$. The agent's objective is to attain

  $$V_{0}(w):=\sup E\left\{\sum_{t=0}^{T-1} \beta^{t} U\left(c_{t}\right)+\beta^{T} U_{T}\left(w_{T}\right) \mid w_{0}=w\right\},$$

  where the supremum is taken over all adapted sequences $\left(c_{t}\right)$. If the value function is defined for $0 \leqslant n<T$ by

  $$V_{n}(w)=\sup E\left\{\sum_{t=n}^{T-1} \beta^{t-n} U\left(c_{t}\right)+\beta^{T-n} U_{T}\left(w_{T}\right) \mid w_{n}=w\right\}$$

  with $V_{T}=U_{T}$, explain briefly why you expect the $V_{n}$ to satisfy

  $$V_{n}(w)=\sup _{c}\left[U(c)+\beta E\left\{V_{n+1}\left((1+r)(w-c)+\varepsilon_{n+1}\right)\right\}\right]$$

  Show that the solution to $(*)$ has the form

  $$V_{n}(w)=-A_{n} \exp (-\nu w),$$

  for constants $A_{n}$ to be identified. What is the form of the consumption choices that achieve the supremum in $(*)$ ?

  comment

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2013

  Let $S_{t}:=\left(S_{t}^{1}, S_{t}^{2}, \ldots, S_{t}^{n}\right)^{\mathrm{T}}$ denote the time- $t$ prices of $n$ risky assets in which an agent may invest, $t=0,1$. He may also invest his money in a bank account, which will return interest at rate $r>0$. At time 0 , he knows $S_{0}$ and $r$, and he knows that $S_{1} \sim N(\mu, V)$. If he chooses at time 0 to invest cash value $\theta_{i}$ in risky asset $i$, express his wealth $w_{1}$ at time 1 in terms of his initial wealth $w_{0}>0$, the choices $\theta:=\left(\theta_{1}, \ldots, \theta_{n}\right)^{\mathrm{T}}$, the value of $S_{1}$, and $r$.

  Suppose that his goal is to minimize the variance of $w_{1}$ subject to the requirement that the mean $E\left(w_{1}\right)$ should be at least $m$, where $m \geqslant(1+r) w_{0}$ is given. What portfolio $\theta$ should he choose to achieve this?

  Suppose instead that his goal is to minimize $E\left(w_{1}^{2}\right)$ subject to the same constraint. Show that his optimal portfolio is unchanged.

  comment

Topics in Analysis

• Paper 1, Section I, $2 F$

  Topics in Analysis | Part II, 2013

  Show that $\sin (1)$ is irrational. [The angle is measured in radians.]

  comment

• Paper 2, Section I, F

  Topics in Analysis | Part II, 2013

  (i) Show that for every $\epsilon>0$ there is a polynomial $p: \mathbb{R} \rightarrow \mathbb{R}$ such that $\left|\frac{1}{x}-p(x)\right| \leqslant \epsilon$ for all $x \in \mathbb{R}$ satisfying $\frac{1}{2} \leqslant|x| \leqslant 2$.

  [You may assume standard results provided they are stated clearly.]

  (ii) Show that there is no polynomial $p: \mathbb{C} \rightarrow \mathbb{C}$ such that $\left|\frac{1}{z}-p(z)\right|<1$ for all $z \in \mathbb{C}$ satisfying $\frac{1}{2} \leqslant|z| \leqslant 2$.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2013

  (i) Let $n \geqslant 4$ be an integer. Show that

  $$1+\frac{1}{n+\frac{1}{1+\frac{1}{n+\ldots}}} \geqslant 1+\frac{1}{2 n} .$$

  (ii) Let us say that an irrational number $\alpha$ is badly approximable if there is some constant $c>0$ such that

  $$\left|\alpha-\frac{p}{q}\right| \geqslant \frac{c}{q^{2}}$$

  for all $q \geqslant 1$ and for all integers $p$. Show that if the integers $a_{n}$ in the continued fraction expansion $\alpha=\left[a_{0}, a_{1}, a_{2}, \ldots\right]$ are bounded then $\alpha$ is badly approximable.

  Give, with proof, an example of an irrational number which is not badly approximable.

  [Standard facts about continued fractions may be used without proof provided they are stated clearly.]

  comment

• Paper 3, Section I, $2 F$

  Topics in Analysis | Part II, 2013

  State Brouwer's fixed point theorem. Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ be a continuous function with the property that $|f(x)-x| \leqslant 1$ for all $x$. Show that $f$ is surjective.

  comment

• Paper 3, Section II, F

  Topics in Analysis | Part II, 2013

  Suppose that $x_{0}, x_{1}, \ldots, x_{n} \in[-1,1]$ are distinct points. Let $f$ be an infinitely differentiable real-valued function on an open interval containing $[-1,1]$. Let $p$ be the unique polynomial of degree at most $n$ such that $f\left(x_{r}\right)=p\left(x_{r}\right)$ for $r=0,1, \ldots, n$. Show that for each $x \in[-1,1]$ there is some $\xi \in(-1,1)$ such that

  $$f(x)-p(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right) \ldots\left(x-x_{n}\right)$$

  Now take $x_{r}=\cos \frac{2 r+1}{2 n+2} \pi$. Show that

  $$|f(x)-p(x)| \leqslant \frac{1}{2^{n}(n+1) !} \sup _{\xi \in[-1,1]}\left|f^{(n+1)}(\xi)\right|$$

  for all $x \in[-1,1]$. Deduce that there is a polynomial $p$ of degree at most $n$ such that

  $$\left|\frac{1}{3+x}-p(x)\right| \leqslant \frac{1}{4^{n+1}}$$

  for all $x \in[-1,1]$.

  comment

• Paper 4, Section I, F

  Topics in Analysis | Part II, 2013

  State the Baire Category Theorem. A set $X \subseteq \mathbb{R}$ is said to be a $G_{\delta}$-set if it is the intersection of countably many open sets. Show that the set $\mathbb{Q}$ of rationals is not a $G_{\delta}$-set.

  [You may assume that the rationals are countable and that $\mathbb{R}$ is complete.]

  comment

Waves

• Paper 1, Section II, 39C

  Waves | Part II, 2013

  Starting from the equations for the one-dimensional unsteady flow of a perfect gas of uniform entropy, show that the Riemann invariants

  $$R_{\pm}=u \pm \frac{2}{\gamma-1}\left(c-c_{0}\right)$$

  are constant on characteristics $C_{\pm}$given by $d x / d t=u \pm c$, where $u(x, t)$ is the velocity of the gas, $c(x, t)$ is the local speed of sound, $c_{0}$ is a constant and $\gamma$ is the ratio of specific heats.

  Such a gas initially occupies the region $x>0$ to the right of a piston in an infinitely long tube. The gas and the piston are initially at rest with $c=c_{0}$. At time $t=0$ the piston starts moving to the left at a constant velocity $V$. Find $u(x, t)$ and $c(x, t)$ in the three regions

  $$\begin{array}{cc} \text { (i) } & c_{0} t \leqslant x \\ \text { (ii) } & a t \leqslant x \leqslant c_{0} t \\ \text { (iii) } & -V t \leqslant x \leqslant a t, \end{array}$$

  where $a=c_{0}-\frac{1}{2}(\gamma+1) V$. What is the largest value of $V$ for which $c$ is positive throughout region (iii)? What happens if $V$ exceeds this value?

  comment

• Paper 2, Section II, C

  Waves | Part II, 2013

  Show that the equations governing linear elasticity have plane-wave solutions, distinguishing between $\mathrm{P}, \mathrm{SV}$ and $\mathrm{SH}$ waves.

  A semi-infinite elastic medium in $y<0$ (where $y$ is the vertical coordinate) with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ is overlaid by a layer of thickness $h($ in $0<y<h)$ of a second elastic medium with density $\rho^{\prime}$ and Lamé moduli $\lambda^{\prime}$ and $\mu^{\prime}$. The top surface at $y=h$ is free, that is, the surface tractions vanish there. The speed of the S-waves is lower in the layer, that is, $c_{S}^{\prime 2}=\mu^{\prime} / \rho^{\prime}<\mu / \rho=c_{S}^{2}$. For a time-harmonic SH-wave with horizontal wavenumber $k$ and frequency $\omega$, which oscillates in the slow top layer and decays exponentially into the fast semi-infinite medium, derive the dispersion relation for the apparent horizontal wave speed $c(k)=\omega / k$ :

  $$\tan \left(k h \sqrt{\left(c^{2} / c_{S}^{\prime 2}\right)-1}\right)=\frac{\mu \sqrt{1-\left(c^{2} / c_{S}^{2}\right)}}{\mu^{\prime} \sqrt{\left(c^{2} / c_{S}^{\prime 2}\right)-1}}$$

  Show graphically that for a given value of $k$ there is always at least one real value of $c$ which satisfies equation $(*)$. Show further that there are one or more higher modes if $\sqrt{c_{S}^{2} / c_{S}^{\prime 2}-1}>\pi / k h .$

  comment

• Paper 3, Section II, C

  Waves | Part II, 2013

  The dispersion relation for sound waves of frequency $\omega$ in a stationary homogeneous gas is $\omega=c_{0}|\mathbf{k}|$, where $c_{0}$ is the speed of sound and $\mathbf{k}$ is the wavenumber. Derive the dispersion relation for sound waves of frequency $\omega$ in a uniform flow with velocity U.

  For a slowly-varying medium with local dispersion relation $\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$, derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  explaining carefully the meaning of the notation used.

  Suppose that two-dimensional sound waves with initial wavenumber $\left(k_{0}, l_{0}, 0\right)$ are generated at the origin in a gas occupying the half-space $y>0$. If the gas has a slowlyvarying mean velocity $(\gamma y, 0,0)$, where $\gamma>0$, show:

  (a) that if $k_{0}>0$ and $l_{0}>0$ the waves reach a maximum height (which should be identified), and then return to the level $y=0$ in a finite time;

  (b) that if $k_{0}<0$ and $l_{0}>0$ then there is no bound on the height to which the waves propagate.

  Comment briefly on the existence, or otherwise, of a quiet zone.

  comment

• Paper 4, Section II, 38C

  Waves | Part II, 2013

  A wave disturbance satisfies the equation

  $$\frac{\partial^{2} \psi}{\partial t^{2}}-c^{2} \frac{\partial^{2} \psi}{\partial x^{2}}+c^{2} \psi=0$$

  where $c$ is a positive constant. Find the dispersion relation, and write down the solution to the initial-value problem for which $\partial \psi / \partial t(x, 0)=0$ for all $x$, and $\psi(x, 0)$ is given in the form

  $$\psi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  where $A(k)$ is a real function with $A(k)=A(-k)$, so that $\psi(x, 0)$ is real and even.

  Use the method of stationary phase to obtain an approximation to $\psi(x, t)$ for large $t$, with $x / t$ taking the constant value $V$, and $0 \leqslant V<c$. Explain briefly why your answer is inappropriate if $V>c$.

  [You are given that

  $$\left.\int_{-\infty}^{\infty} \exp \left(i u^{2}\right) d u=\pi^{1 / 2} e^{i \pi / 4} .\right]$$

  comment