Part II, 2005, Paper 4

Algebraic Topology

• 4.II.21H

  Algebraic Topology | Part II, 2005

  Let $X$ be a simplicial complex. Suppose $X=B \cup C$ for subcomplexes $B$ and $C$, and let $A=B \cap C$. Show that the inclusion of $A$ in $B$ induces an isomorphism $H_{*} A \rightarrow H_{*} B$ if and only if the inclusion of $C$ in $X$ induces an isomorphism $H_{*} C \rightarrow H_{*} X$.

  comment

Applications of Quantum Mechanics

• 4.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  A semiconductor has a valence energy band with energies $E \leqslant 0$ and density of states $g_{v}(E)$, and a conduction energy band with energies $E \geqslant E_{g}$ and density of states $g_{c}(E)$. Assume that $g_{v}(E) \sim A_{v}(-E)^{\frac{1}{2}}$ as $E \rightarrow 0$, and that $g_{c}(E) \sim A_{c}\left(E-E_{g}\right)^{\frac{1}{2}}$ as $E \rightarrow E_{g}$. At zero temperature all states in the valence band are occupied and the conduction band is empty. Let $p$ be the number of holes in the valence band and $n$ the number of electrons in the conduction band at temperature $T$. Under suitable approximations derive the result

  $$p n=N_{v} N_{c} e^{-E_{g} / k T}$$

  where

  $$N_{v}=\frac{1}{2} \sqrt{\pi} A_{v}(k T)^{\frac{3}{2}}, \quad N_{c}=\frac{1}{2} \sqrt{\pi} A_{c}(k T)^{\frac{3}{2}} .$$

  Briefly describe how a semiconductor may conduct electricity but with a conductivity that is strongly temperature dependent.

  Describe how doping of the semiconductor leads to $p \neq n$. A $p n$ junction is formed between an $n$-type semiconductor, with $N_{d}$ donor atoms, and a $p$-type semiconductor, with $N_{a}$ acceptor atoms. Show that there is a potential difference $V_{n p}=\Delta E /|e|$ across the junction, where $e$ is the electron charge, and

  $$\Delta E=E_{g}-k T \ln \frac{N_{v} N_{c}}{N_{d} N_{a}} .$$

  Two semiconductors, one $p$-type and one $n$-type, are joined to make a closed circuit with two $p n$ junctions. Explain why a current will flow around the circuit if the junctions are at different temperatures.

  [The Fermi-Dirac distribution function at temperature $T$ and chemical potential $\mu$ is $\frac{g(E)}{e^{(E-\mu) / k T}+1}$, where $g(E)$ is the number of states with energy $E$.

  Note that $\int_{0}^{\infty} x^{\frac{1}{2}} e^{-x} d x=\frac{1}{2} \sqrt{\pi}$.]

  comment

Applied Probability

• 4.II.26I

  Applied Probability | Part II, 2005

  A particle performs a continuous-time nearest neighbour random walk on a regular triangular lattice inside an angle $\pi / 3$, starting from the corner. See the diagram below. The jump rates are $1 / 3$ from the corner and $1 / 6$ in each of the six directions if the particle is inside the angle. However, if the particle is on the edge of the angle, the rate is $1 / 3$ along the edge away from the corner and $1 / 6$ to each of three other neighbouring sites in the angle. See the diagram below, where a typical trajectory is also shown.

  

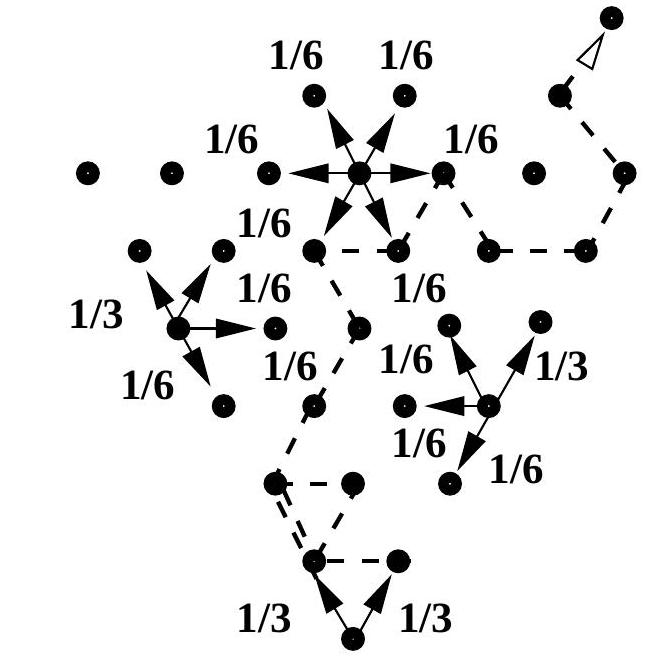
  The particle position at time $t \geqslant 0$ is determined by its vertical level $V_{t}$ and its horizontal position $G_{t}$. For $k \geqslant 0$, if $V_{t}=k$ then $G_{t}=0, \ldots, k$. Here $1, \ldots, k-1$ are positions inside, and 0 and $k$ positions on the edge of the angle, at vertical level $k$.

  Let $J_{1}^{V}, J_{2}^{V}, \ldots$ be the times of subsequent jumps of process $\left(V_{t}\right)$ and consider the embedded discrete-time Markov chains

  $$Y_{n}^{\text {in }}=\left(\widehat{G}_{n}^{\text {in }}, \widehat{V}_{n}\right) \text { and } Y_{n}^{\text {out }}=\left(\widehat{G}_{n}^{\text {out }}, \widehat{V}_{n}\right)$$

  where $\widehat{V}_{n}$ is the vertical level immediately after time $J_{n}^{V}, \widehat{G}_{n}^{\text {in }}$ is the horizontal position immediately after time $J_{n}^{V}$, and $\widehat{G}_{n}^{\text {out }}$ is the horizontal position immediately before time $J_{n+1}^{V}$. (a) Assume that $\left(\widehat{V}_{n}\right)$ is a Markov chain with transition probabilities

  $$\mathbb{P}\left(\widehat{V}_{n}=k+1 \mid \widehat{V}_{n-1}=k\right)=\frac{k+2}{2(k+1)}, \mathbb{P}\left(\widehat{V}_{n}=k-1 \mid \widehat{V}_{n-1}=k\right)=\frac{k}{2(k+1)},$$

  and that $\left(V_{t}\right)$ is a continuous-time Markov chain with rates

  $$q_{k k-1}=\frac{k}{3(k+1)}, \quad q_{k k}=-\frac{2}{3}, \quad q_{k k+1}=\frac{k+2}{3(k+1)}$$

  [You will be asked to justify these assumptions in part (b) of the question.] Determine whether the chains $\left(\widehat{V}_{n}\right)$ and $\left(V_{t}\right)$ are transient, positive recurrent or null recurrent.

  (b) Now assume that, conditional on $\widehat{V}_{n}=k$ and previously passed vertical levels, the horizontal positions $\widehat{G}_{n}^{\text {in }}$ and $\widehat{G}_{n}^{\text {out }}$ are uniformly distributed on $\{0, \ldots, k\}$. In other words, for all attainable values $k, k_{n-1}, \ldots, k_{1}$ and for all $i=0, \ldots, k$,

  $$\begin{aligned} &\mathbb{P}\left(\widehat{G}_{n}^{\text {in }}=i \mid \widehat{V}_{n}=k, \widehat{V}_{n-1}=k_{n-1}, \ldots, \widehat{V}_{1}=k_{1}, \widehat{V}_{0}=0\right) \\ &\quad=\mathbb{P}\left(\widehat{G}_{n}^{\text {out }}=i \mid \widehat{V}_{n}=k, \widehat{V}_{n-1}=k_{n-1}, \ldots, \widehat{V}_{1}=k_{1}, \widehat{V}_{0}=0\right)=\frac{1}{k+1} \end{aligned}$$

  Deduce that $\left(\widehat{V}_{n}\right)$ and $\left(V_{t}\right)$ are indeed Markov chains with transition probabilities and rates as in (a).

  (c) Finally, prove property $(*)$.

  comment

Asymptotic Methods

• 4.II $. 31 \mathrm{~A}$

  Asymptotic Methods | Part II, 2005

  Consider the differential equation

  $$\frac{d^{2} w}{d x^{2}}=q(x) w$$

  where $q(x) \geqslant 0$ in an interval $(a, \infty)$. Given a solution $w(x)$ and a further smooth function $\xi(x)$, define

  $$W(x)=\left[\xi^{\prime}(x)\right]^{1 / 2} w(x) .$$

  Show that, when $\xi$ is regarded as the independent variable, the function $W(\xi)$ obeys the differential equation

  $$\frac{d^{2} W}{d \xi^{2}}=\left\{\dot{x}^{2} q(x)+\dot{x}^{1 / 2} \frac{d^{2}}{d \xi^{2}}\left[\dot{x}^{-1 / 2}\right]\right\} W$$

  where $\dot{x}$ denotes $d x / d \xi$.

  Taking the choice

  $$\xi(x)=\int q^{1 / 2}(x) d x$$

  show that equation $(*)$ becomes

  $$\frac{d^{2} W}{d \xi^{2}}=(1+\phi) W$$

  where

  $$\phi=-\frac{1}{q^{3 / 4}} \frac{d^{2}}{d x^{2}}\left(\frac{1}{q^{1 / 4}}\right)$$

  In the case that $\phi$ is negligible, deduce the Liouville-Green approximate solutions

  $$w_{\pm}=q^{-1 / 4} \exp \left(\pm \int q^{1 / 2} d x\right)$$

  Consider the Whittaker equation

  $$\frac{d^{2} w}{d x^{2}}=\left[\frac{1}{4}+\frac{s(s-1)}{x^{2}}\right] w$$

  where $s$ is a real constant. Show that the Liouville-Green approximation suggests the existence of solutions $w_{A, B}(x)$ with asymptotic behaviour of the form

  $$w_{A} \sim \exp (x / 2)\left(1+\sum_{n=1}^{\infty} a_{n} x^{-n}\right), \quad w_{B} \sim \exp (-x / 2)\left(1+\sum_{n=1}^{\infty} b_{n} x^{-n}\right)$$

  as $x \rightarrow \infty$.

  Given that these asymptotic series may be differentiated term-by-term, show that

  $$a_{n}=\frac{(-1)^{n}}{n !}(s-n)(s-n+1) \ldots(s+n-1) \text {. }$$

  comment

Classical Dynamics

• 4.I.9C

  Classical Dynamics | Part II, 2005

  Define a canonical transformation for a one-dimensional system with coordinates $(q, p) \rightarrow(Q, P)$. Show that if the transformation is canonical then $\{Q, P\}=1$.

  Find the values of constants $\alpha$ and $\beta$ such that the following transformations are canonical: (i) $Q=p q^{\beta}, P=\alpha q^{-1}$. (ii) $Q=q^{\alpha} \cos (\beta p), P=q^{\alpha} \sin (\beta p)$.

  comment

Coding and Cryptography

• 4.I.4J

  Coding and Cryptography | Part II, 2005

  What does it mean to transmit reliably at rate $r$ through a binary symmetric channel (BSC) with error probability $p$ ? Assuming Shannon's second coding theorem, compute the supremum of all possible reliable transmission rates of a BSC. What happens if (i) $p$ is very small, (ii) $p=1 / 2$, or (iii) $p>1 / 2$ ?

  comment

Cosmology

• 4.I.10D

  Cosmology | Part II, 2005

  The linearised equation for the growth of a density fluctuation $\delta_{k}$ in a homogeneous and isotropic universe is

  $$\frac{d^{2} \delta_{k}}{d t^{2}}+2 \frac{\dot{a}}{a} \frac{d \delta_{k}}{d t}-\left(4 \pi G \rho_{\mathrm{m}}-\frac{v_{s}^{2} k^{2}}{a^{2}}\right) \delta_{k}=0,$$

  where $\rho_{\mathrm{m}}$ is the non-relativistic matter density, $k$ is the comoving wavenumber and $v_{s}$ is the sound speed $\left(v_{s}^{2} \equiv d P / d \rho\right)$.

  (a) Define the Jeans length $\lambda_{\mathrm{J}}$ and discuss its significance for perturbation growth.

  (b) Consider an Einstein-de Sitter universe with $a(t)=\left(t / t_{0}\right)^{2 / 3}$ filled with pressure-free matter $(P=0)$. Show that the perturbation equation $(*)$ can be re-expressed as

  $$\ddot{\delta}_{k}+\frac{4}{3 t} \dot{\delta}_{k}-\frac{2}{3 t^{2}} \delta_{k}=0 .$$

  By seeking power law solutions, find the growing and decaying modes of this equation.

  (c) Qualitatively describe the evolution of non-relativistic matter perturbations $(k>a H)$ in the radiation era, $a(t) \propto t^{1 / 2}$, when $\rho_{\mathrm{r}} \gg \rho_{\mathrm{m}}$. What feature in the power spectrum is associated with the matter-radiation transition?

  comment

• 4.II.15D

  Cosmology | Part II, 2005

  For an ideal gas of bosons, the average occupation number can be expressed as

  $$\bar{n}_{k}=\frac{g_{k}}{e^{\left(E_{k}-\mu\right) / k T}-1},$$

  where $g_{k}$ has been included to account for the degeneracy of the energy level $E_{k}$. In the approximation in which a discrete set of energies $E_{k}$ is replaced with a continuous set with momentum $p$, the density of one-particle states with momentum in the range $p$ to $p+d p$ is $g(p) d p$. Explain briefly why

  $$g(p) \propto p^{2} V,$$

  where $V$ is the volume of the gas. Using this formula with equation $(*)$, obtain an expression for the total energy density $\epsilon=E / V$ of an ultra-relativistic gas of bosons at zero chemical potential as an integral over $p$. Hence show that

  $$\epsilon \propto T^{\alpha}$$

  where $\alpha$ is a number you should find. Why does this formula apply to photons?

  Prior to a time $t \sim 100,000$ years, the universe was filled with a gas of photons and non-relativistic free electrons and protons. Subsequently, at around $t \sim 400,000$ years, the protons and electrons began combining to form neutral hydrogen,

  $$p+e^{-} \leftrightarrow H+\gamma$$

  Deduce Saha's equation for this recombination process stating clearly the steps required:

  $$\frac{n_{\mathrm{e}}^{2}}{n_{\mathrm{H}}}=\left(\frac{2 \pi m_{\mathrm{e}} k T}{h^{2}}\right)^{3 / 2} \exp (-I / k T)$$

  where $I$ is the ionization energy of hydrogen. [Note that the equilibrium number density of a non-relativistic species $\left(k T \ll m c^{2}\right)$ is given by $n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left[\left(\mu-m c^{2}\right) / k T\right]$, while the photon number density is $n_{\gamma}=16 \pi \zeta(3)\left(\frac{k T}{h c}\right)^{3}$, where $\left.\zeta(3) \approx 1.20 \ldots\right]$

  Consider now the fractional ionization $X_{\mathrm{e}}=n_{\mathrm{e}} / n_{\mathrm{B}}$, where $n_{B}=n_{\mathrm{p}}+n_{\mathrm{H}}=\eta n_{\gamma}$ is the baryon number of the universe and $\eta$ is the baryon-to-photon ratio. Find an expression for the ratio

  $$\left(1-X_{\mathrm{e}}\right) / X_{\mathrm{e}}^{2}$$

  in terms only of $k T$ and constants such as $\eta$ and $I$. One might expect neutral hydrogen to form at a temperature given by $k T \approx I \approx 13 \mathrm{eV}$, but instead in our universe it forms at the much lower temperature $k T \approx 0.3 \mathrm{eV}$. Briefly explain why.

  comment

Differential Geometry

• 4.II.24H

  Differential Geometry | Part II, 2005

  (i) Define what is meant by an isothermal parametrization. Let $\phi: U \rightarrow \mathbb{R}^{3}$ be an isothermal parametrization. Prove that

  $$\phi_{u u}+\phi_{v v}=2 \lambda^{2} \mathbf{H}$$

  where $\mathbf{H}$ is the mean curvature vector and $\lambda^{2}=\left\langle\phi_{u}, \phi_{u}\right\rangle$.

  Define what it means for $\phi$ to be minimal, and deduce that $\phi$ is minimal if and only if $\Delta \phi=0$.

  [You may assume that the mean curvature $H$ can be written as

  $$\left.H=\frac{e G-2 f F+g E}{2\left(E G-F^{2}\right)} .\right]$$

  (ii) Write $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$. Consider the complex valued functions

  $$\varphi_{1}=x_{u}-i x_{v}, \quad \varphi_{2}=y_{u}-i y_{v}, \quad \varphi_{3}=z_{u}-i z_{v}$$

  Show that $\phi$ is isothermal if and only if $\varphi_{1}^{2}+\varphi_{2}^{2}+\varphi_{3}^{2} \equiv 0$.

  Suppose now that $\phi$ is isothermal. Prove that $\phi$ is minimal if and only if $\varphi_{1}, \varphi_{2}$ and $\varphi_{3}$ are holomorphic functions.

  (iii) Consider the immersion $\phi: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}$ given by

  $$\phi(u, v)=\left(u-u^{3} / 3+u v^{2},-v+v^{3} / 3-u^{2} v, u^{2}-v^{2}\right)$$

  Find $\varphi_{1}, \varphi_{2}$ and $\varphi_{3}$. Show that $\phi$ is an isothermal parametrization of a minimal surface.

  comment

Dynamical Systems

• 4.I.7B

  Dynamical Systems | Part II, 2005

  Find and classify the fixed points of the system

  $$\begin{aligned} &\dot{x}=x(1-y) \\ &\dot{y}=-y+x^{2} . \end{aligned}$$

  Sketch the phase plane.

  What is the $\omega$-limit for the point $(2,-1)$ ? Which points have $(0,0)$ as their $\omega$-limit?

  comment

Electrodynamics

• 4.II $. 35 \mathrm{~B} \quad$

  Electrodynamics | Part II, 2005

  In Ginzburg-Landau theory, superconductivity is due to "supercarriers" of mass $m_{s}$ and charge $q_{s}$, which are described by a macroscopic wavefunction $\psi$ with "Mexican hat" potential

  $$V=\alpha(T)|\psi|^{2}+\frac{1}{2} \beta|\psi|^{4}$$

  Here, $\beta>0$ is constant and $\alpha(T)$ is a function of temperature $T$ such that $\alpha(T)>0$ for $T>T_{c}$ but $\alpha(T)<0$ for $T<T_{c}$, where $T_{c}$ is a critical temperature. In the presence of a magnetic field $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$, the total energy of the superconducting system is

  $$E\left[\psi, \psi^{*}, \mathbf{A}\right]=\int d^{3} x\left[\frac{1}{2 \mu_{0}} A_{k, j}\left(A_{k, j}-A_{j, k}\right)+\frac{\hbar^{2}}{2 m_{s}}\left|\psi_{, k}+i \frac{q_{s}}{\hbar} A_{k} \psi\right|^{2}+V\right]$$

  Use this to derive the equations

  $$-\frac{\hbar^{2}}{2 m_{s}}\left(\nabla-i \frac{q_{s}}{\hbar} \mathbf{A}\right)^{2} \psi+\left(\alpha+\beta|\psi|^{2}\right) \psi=0$$

  and

  $$\boldsymbol{\nabla} \times \mathbf{B} \equiv \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{A})-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{j}$$

  where

  $$\begin{aligned} \mathbf{j} &=-\frac{i q_{s} \hbar}{2 m_{s}}\left(\psi^{*} \boldsymbol{\nabla} \psi-\psi \boldsymbol{\nabla} \psi^{*}\right)-\frac{q_{s}^{2}}{m_{s}}|\psi|^{2} \mathbf{A} \\ &=\frac{q_{s}}{2 m_{s}}\left[\psi^{*}\left(-i \hbar \boldsymbol{\nabla}-q_{s} \mathbf{A}\right) \psi+\psi\left(i \hbar \boldsymbol{\nabla}-q_{s} \mathbf{A}\right) \psi^{*}\right] \end{aligned}$$

  Suppose that we write the wavefunction as

  $$\psi=\sqrt{n_{s}} e^{i \theta}$$

  where $n_{s}$ is the (real positive) supercarrier density and $\theta$ is a real phase function. Given that

  $$\left(\boldsymbol{\nabla}-\frac{i q_{s}}{\hbar} \mathbf{A}\right) \psi=0$$

  show that $n_{s}$ is constant and that $\hbar \boldsymbol{\nabla} \theta=q_{s} \mathbf{A}$. Given also that $T<T_{c}$, deduce that (*) allows such solutions for a certain choice of $n_{s}$, which should be determined. Verify that your results imply $\mathbf{j}=\mathbf{0}$. Show also that $\mathbf{B}=\mathbf{0}$ and hence that ( $\dagger$ ) is solved.

  Let $\mathcal{S}$ be a surface within the superconductor with closed boundary $\mathcal{C}$. Show that the magnetic flux through $\mathcal{S}$ is

  $$\Phi \equiv \int_{\mathcal{S}} \mathbf{B} \cdot \mathbf{d} \mathbf{S}=\frac{\hbar}{q_{s}}[\theta]_{\mathcal{C}}$$

  Discuss, briefly, flux quantization.

  comment

Fluid Dynamics II

• 4.II.37E

  Fluid Dynamics II | Part II, 2005

  Consider flow of an incompressible fluid of uniform density $\rho$ and dynamic viscosity $\mu$. Show that the rate of viscous dissipation per unit volume is given by

  $$\Phi=2 \mu e_{i j} e_{i j},$$

  where $e_{i j}$ is the strain rate.

  Determine expressions for $e_{i j}$ and $\Phi$ when the flow is irrotational with velocity potential $\phi$. Hence determine the rate of viscous dissipation, averaged over a wave period $2 \pi / \omega$, for an irrotational two-dimensional surface wave of wavenumber $k$ and small amplitude $a \ll k^{-1}$ in a fluid of very small viscosity $\mu \ll \rho \omega / k^{2}$ and great depth $H \gg 1 / k$.

  [You may use without derivation that in deep water a linearised wave with surface displacement $\eta=a \cos (k x-w t)$ has velocity potential $\phi=-(\omega a / k) e^{-k z} \sin (k x-\omega t)$.]

  Calculate the depth-integrated time-averaged kinetic energy per wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order like $e^{-\gamma t}$, where

  $$\gamma=4 \mu k^{2} / \rho$$

  comment

Further Complex Methods

• 4.I.8A

  Further Complex Methods | Part II, 2005

  Write down necessary and sufficient conditions on the functions $p(z)$ and $q(z)$ for the point $z=0$ to be (i) an ordinary point and (ii) a regular singular point of the equation

  $$w^{\prime \prime}+p(z) w^{\prime}+q(z) w=0 .$$

  Show that the point $z=\infty$ is an ordinary point if and only if

  $$p(z)=2 z^{-1}+z^{-2} P\left(z^{-1}\right), \quad q(z)=z^{-4} Q\left(z^{-1}\right),$$

  where $P$ and $Q$ are analytic in a neighbourhood of the origin.

  Find the most general equation of the form $(*)$ that has a regular singular point at $z=0$ but no other singular points.

  comment

• 4.II.14A

  Further Complex Methods | Part II, 2005

  Two representations of the zeta function are

  $$\zeta(z)=\frac{\Gamma(1-z)}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \frac{t^{z-1}}{e^{-t}-1} d t \quad \text { and } \quad \zeta(z)=\sum_{1}^{\infty} n^{-z}$$

  where, in the integral representation, the path is the Hankel contour and the principal branch of $t^{z-1}$, for which $|\arg z|<\pi$, is to be used. State the range of $z$ for which each representation is valid.

  Evaluate the integral

  $$\int_{\gamma} \frac{t^{z-1}}{e^{-t}-1} d t$$

  where $\gamma$ is a closed path consisting of the straight line $z=\pi i+x$, with $|x|<2 N \pi$, and the semicircle $|z-\pi i|=2 N \pi$, with $\operatorname{Im} z>\pi$, where $N$ is a positive integer.

  Making use of this result and assuming, when necessary, that the integral along the curved part of $\gamma$ is negligible when $N$ is large, derive the functional equation

  $$\zeta(z)=2^{z} \pi^{z-1} \sin (\pi z / 2) \Gamma(1-z) \zeta(1-z)$$

  for $z \neq 1$.

  comment

Galois Theory

• 4.II.18G

  Galois Theory | Part II, 2005

  (i) Let $K$ be the splitting field of the polynomial

  $$x^{4}-4 x^{2}-1$$

  over $\mathbb{Q}$. Show that $[K: \mathbb{Q}]=8$, and hence show that the Galois group of $K / \mathbb{Q}$ is the dihedral group of order 8 .

  (ii) Let $L$ be the splitting field of the polynomial

  $$x^{4}-4 x^{2}+1$$

  over $\mathbb{Q}$. Show that $[L: \mathbb{Q}]=4$. Show that the Galois group of $L / \mathbb{Q}$ is $C_{2} \times C_{2}$.

  comment

General Relativity

• 4.II.36C

  General Relativity | Part II, 2005

  State clearly, but do not prove, Birkhoff's Theorem about spherically symmetric spacetimes. Let $(r, \theta, \phi)$ be standard spherical polar coordinates and define $F(r)=$ $1-2 M / r$, where $M$ is a constant. Consider the metric

  $$d s^{2}=\frac{d r^{2}}{F(r)}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-F(r) d t^{2}$$

  Explain carefully why this is appropriate for the region outside a spherically symmetric star that is collapsing to form a black hole.

  By considering radially infalling timelike geodesics $x^{a}=(r(\tau), 0,0, t(\tau))$, where $\tau$ is proper time along the curve, show that a freely falling observer will reach the event horizon after a finite proper time. Show also that a distant observer would see the horizon crossing only after an infinite time.

  comment

Geometry of Group Actions

• 4.I.3G

  Geometry of Group Actions | Part II, 2005

  Show that a set $F \subset \mathbb{R}^{n}$ with Hausdorff dimension strictly less than one is totally disconnected.

  What does it mean for a Möbius transformation to pair two discs? By considering a pair of disjoint discs and a pair of tangent discs, or otherwise, explain in words why there is a 2-generator Schottky group with limit set $\Lambda \subset \mathbb{S}^{2}$ which has Hausdorff dimension at least 1 but which is not homeomorphic to a circle.

  comment

• 4.II.12G

  Geometry of Group Actions | Part II, 2005

  For real $s \geqslant 0$ and $F \subset \mathbb{R}^{n}$, give a careful definition of the $s$-dimensional Hausdorff measure of $F$ and of the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of $F$.

  For $1 \leqslant i \leqslant k$, suppose $S_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is a similarity with contraction factor $c_{i} \in(0,1)$. Prove there is a unique non-empty compact invariant set $I$ for the $\left\{S_{i}\right\}$. State a formula for the Hausdorff dimension of $I$, under an assumption on the $S_{i}$ you should state.

  Hence show the Hausdorff dimension of the fractal $F$ given by iterating the scheme below (at each stage replacing each edge by a new copy of the generating template) is $\operatorname{dim}_{H}(F)=3 / 2$.

  

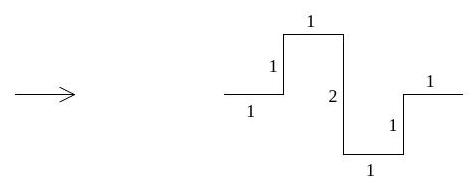
  [Numbers denote lengths]

  comment

Graph Theory

• 4.II.17F

  Graph Theory | Part II, 2005

  Write an essay on extremal graph theory. Your essay should include the proof of at least one extremal theorem. You should state the Erdős-Stone theorem, as well as describing its proof and showing how it can be applied.

  comment

Linear Analysis

• 4.II.22F

  Linear Analysis | Part II, 2005

  Let $X$ and $Y$ be normed vector spaces. Show that a linear map $T: X \rightarrow Y$ is continuous if and only if it is bounded.

  Now let $X, Y, Z$ be Banach spaces. We say that a map $F: X \times Y \rightarrow Z$ is bilinear

  $$\begin{aligned} &F(\alpha x+\beta y, z)=\alpha F(x, z)+\beta F(y, z), \text { for all scalars } \alpha, \beta \text { and } x, y \in X, z \in Y \\ &F(x, \alpha y+\beta z)=\alpha F(x, y)+\beta F(x, z), \text { for all scalars } \alpha, \beta \text { and } x \in X, y, z \in Y . \end{aligned}$$

  Suppose that $F$ is bilinear and is continuous in each variable separately. Show that there exists a constant $M \geqslant 0$ such that

  $$\|F(x, y)\| \leqslant M\|x\|\|y\|$$

  for all $x \in X, y \in Y$.

  [Hint: For each fixed $x \in X$, consider the map $y \mapsto F(x, y)$ from $Y$ to $Z$.]

  comment

Logic and Set Theory

• 4.II.16F

  Logic and Set Theory | Part II, 2005

  State and prove the Completeness Theorem for Propositional Logic. [You do not need to give definitions of the various terms involved. You may assume that the set of primitive propositions is countable. You may also assume the Deduction Theorem, provided that you state it clearly.]

  Where in your argument have you used the third axiom, namely $(\neg \neg p) \Rightarrow p ?$

  State the Compactness Theorem, and deduce it from the Completeness Theorem.

  comment

Mathematical Biology

• 4.I.6E

  Mathematical Biology | Part II, 2005

  The output of a linear perceptron is given by $y=\mathbf{w} \cdot \mathbf{x}$, where $\mathbf{w}$ is a vector of weights connecting a fluctuating input vector $x$ to an output unit. The weights are given random initial values and are then updated according to a learning rule that has a time-constant $\tau$ much greater than the fluctuation timescale of the inputs.

  (a) Find the behaviour of $|\mathbf{w}|$ for each of the following two rules (i) $\tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}$ (ii) $\tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}-\alpha y^{2} \mathbf{w}|\mathbf{w}|^{2}$, where $\alpha$ is a positive constant.

  (b) Consider a third learning rule

  $$\text { (iii) } \tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}-\mathbf{w}|\mathbf{w}|^{2} \text {. }$$

  Show that in a steady state the vector of weights satisfies the eigenvalue equation

  $$\mathbf{C w}=\lambda \mathbf{w}$$

  where the matrix $\mathbf{C}$ and eigenvalue $\lambda$ should be identified.

  (c) Comment briefly on the biological implications of the three rules.

  comment

Number Fields

• 4.II.20G

  Number Fields | Part II, 2005

  State Dedekind's theorem on the factorisation of rational primes into prime ideals.

  A rational prime is said to ramify totally in a field with degree $n$ if it is the $n$-th power of a prime ideal in the field. Show that, in the quadratic field $\mathbb{Q}(\sqrt{d})$ with $d$ a squarefree integer, a rational prime ramifies totally if and only if it divides the discriminant of the field.

  Verify that the same holds in the cyclotomic field $\mathbb{Q}(\zeta)$, where $\zeta=e^{2 \pi i / q}$ with $q$ an odd prime, and also in the cubic field $\mathbb{Q}(\sqrt[3]{2})$.

  $[$ The cases $d \equiv 2,3(\bmod 4)$ and $d \equiv 1(\bmod 4)$ for the quadratic field should be carefully distinguished. It can be assumed that $\mathbb{Q}(\zeta)$ has a basis $1, \zeta, \ldots, \zeta^{q-2}$ and discriminant $(-1)^{(q-1) / 2} q^{q-1}$, and that $\mathbb{Q}(\sqrt[3]{2})$ has a basis $1, \sqrt[3]{2},(\sqrt[3]{2})^{2}$ and discriminant $\left.-108 .\right]$

  comment

Number Theory

• 4.I.1H

  Number Theory | Part II, 2005

  If $n$ is an odd integer and $b$ is an integer prime with $n$, state what it means for $n$ to be a pseudoprime to the base $b$. What is a Carmichael number? State a criterion for $n$ to be a Carmichael number and use the criterion to show that:

  (i) Every Carmichael number is the product of at least three distinct primes.

  (ii) 561 is a Carmichael number.

  comment

• 4.II.11H

  Number Theory | Part II, 2005

  (a) Let $N$ be a non-square integer. Describe the integer solutions of the Pell equation $x^{2}-N y^{2}=1$ in terms of the convergents to $\sqrt{N}$. Show that the set of integer solutions forms an abelian group. Denote the addition law in this group by $\circ$; given solutions $\left(x_{0}, y_{0}\right)$ and $\left(x_{1}, y_{1}\right)$, write down an explicit formula for $\left(x_{0}, y_{0}\right) \circ\left(x_{1}, y_{1}\right)$. If $(x, y)$ is a solution, write down an explicit formula for $(x, y) \circ(x, y) \circ(x, y)$ in the group law.

  (b) Find the continued fraction expansion of $\sqrt{11}$. Find the smallest solution in integers $x, y>0$ of the Pell equation $x^{2}-11 y^{2}=1$. Use the formula in Part (a) to compute $(x, y) \circ(x, y) \circ(x, y)$.

  comment

Numerical Analysis

• 4.II.39A

  Numerical Analysis | Part II, 2005

  An $n \times n$ skew-symmetric matrix $A$ is converted into an upper-Hessenberg form $B$, say, by Householder reflections.

  (a) Describe each step of the procedure and observe that $B$ is tridiagonal. Your algorithm should take advantage of the special form of $A$ to reduce the number of computations.

  (b) Compare the cost (counting only products and looking only at the leading term) of converting a skew-symmetric and a symmetric matrix to an upper-Hessenberg form using Householder reflections.

  comment

Optimization and Control

• 4.II.29I

  Optimization and Control | Part II, 2005

  A continuous-time control problem is defined in terms of state variable $x(t) \in \mathbb{R}^{n}$ and control $u(t) \in \mathbb{R}^{m}, 0 \leqslant t \leqslant T$. We desire to minimize $\int_{0}^{T} c(x, t) d t+K(x(T))$, where $T$ is fixed and $x(T)$ is unconstrained. Given $x(0)$ and $\dot{x}=a(x, u)$, describe further boundary conditions that can be used in conjunction with Pontryagin's maximum principle to find $x, u$ and the adjoint variables $\lambda_{1}, \ldots, \lambda_{n}$.

  Company 1 wishes to steal customers from Company 2 and maximize the profit it obtains over an interval $[0, T]$. Denoting by $x_{i}(t)$ the number of customers of Company $i$, and by $u(t)$ the advertising effort of Company 1 , this leads to a problem

  $$\operatorname{minimize} \int_{0}^{T}\left[x_{2}(t)+3 u(t)\right] d t$$

  where $\dot{x}_{1}=u x_{2}, \dot{x}_{2}=-u x_{2}$, and $u(t)$ is constrained to the interval $[0,1]$. Assuming $x_{2}(0)>3 / T$, use Pontryagin's maximum principle to show that the optimal advertising policy is bang-bang, and that there is just one change in advertising effort, at a time $t^{*}$, where

  $$3 e^{t^{*}}=x_{2}(0)\left(T-t^{*}\right) .$$

  comment

Partial Differential Equations

• 4.II.30C

  Partial Differential Equations | Part II, 2005

  Write down the solution of the three-dimensional wave equation

  $$u_{t t}-\Delta u=0, \quad u(0, x)=0, \quad u_{t}(0, x)=g(x),$$

  for a Schwartz function $g$. Here $\Delta$ is taken in the variables $x \in \mathbb{R}^{3}$ and $u_{t}=\partial u / \partial t$ etc. State the "strong" form of Huygens principle for this solution. Using the method of descent, obtain the solution of the corresponding problem in two dimensions. State the "weak" form of Huygens principle for this solution.

  Let $u \in C^{2}\left([0, T] \times \mathbb{R}^{3}\right)$ be a solution of

  $$u_{t t}-\Delta u+|x|^{2} u=0, \quad u(0, x)=0, \quad u_{t}(0, x)=0$$

  Show that

  $$\partial_{t} e+\nabla \cdot \mathbf{p}=0$$

  where

  $$e=\frac{1}{2}\left(u_{t}^{2}+|\nabla u|^{2}+|x|^{2} u^{2}\right), \quad \text { and } \quad \mathbf{p}=-u_{t} \nabla u .$$

  Hence deduce, by integration of $(* *)$ over the region

  $$K=\left\{(t, x): 0 \leqslant t \leqslant t_{0}-a \leqslant t_{0},\left|x-x_{0}\right| \leqslant t_{0}-t\right\}$$

  or otherwise, that $(*)$ satisfies the weak Huygens principle.

  comment

Principles of Quantum Mechanics

• 4.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  The Hamiltonian for a quantum system in the Schrödinger picture is

  $$H_{0}+\lambda V(t),$$

  where $H_{0}$ is independent of time and the parameter $\lambda$ is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Let $|a\rangle$ and $|b\rangle$ be eigenstates of $H_{0}$ with distinct eigenvalues $E_{a}$ and $E_{b}$ respectively. Show that if the system is initially in state $|a\rangle$ then the probability of measuring it to be in state $|b\rangle$ after a time $t$ is

  $$\frac{\lambda^{2}}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle b\left|V\left(t^{\prime}\right)\right| a\right\rangle e^{i\left(E_{b}-E_{a}\right) t^{\prime} / \hbar}\right|^{2}+O\left(\lambda^{3}\right)$$

  Deduce that if $V(t)=e^{-\mu t / \hbar} W$, where $W$ is a time-independent operator and $\mu$ is a positive constant, then the probability for such a transition to have occurred after a very long time is approximately

  $$\frac{\lambda^{2}}{\mu^{2}+\left(E_{b}-E_{a}\right)^{2}}|\langle b|W| a\rangle|^{2}$$

  comment

Principles of Statistics

• 4.II.27I

  Principles of Statistics | Part II, 2005

  A group of $n$ hospitals is to be 'appraised'; the 'performance' $\theta_{i}$ of hospital $i$ has a $N(0,1 / \tau)$ prior distribution, different hospitals being independent. The 'performance' cannot be measured directly, so an expensive firm of management consultants has been hired to arrive at each hospital's Standardised Index of Quality [SIQ], this being a number $X_{i}$ for hospital $i$ related to $\theta_{i}$ by the commercially-sensitive formula

  $$X_{i}=\theta_{i}+\varepsilon_{i}$$

  where the $\varepsilon_{i}$ are independent with common $N\left(0,1 / \tau_{\varepsilon}\right)$ distribution.

  (i) Assume that $\tau$ and $\tau_{\varepsilon}$ are known. What is the posterior distribution of $\theta$ given $X$ ? Suppose that hospital $j$ was the hospital with the lowest SIQ, with a value $X_{j}=x$; conditional on $X$, what is the distribution of $\theta_{j}$ ?

  (ii) Now, instead of assuming $\tau$ and $\tau_{\varepsilon}$ known, suppose that $\tau$ has a Gamma prior with parameters $(\alpha, \beta)$, density

  $$f(t)=(\beta t)^{\alpha-1} \beta e^{-\beta t} / \Gamma(\alpha)$$

  for known $\alpha$ and $\beta$, and that $\tau_{\varepsilon}=\kappa \tau$, where $\kappa$ is a known constant. Find the posterior distribution of $(\theta, \tau)$ given $X$. Comment briefly on the form of the distribution.

  comment

Probability and Measure

• 4.II.25J

  Probability and Measure | Part II, 2005

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be Borel-measurable. State Fubini's theorem for the double integral

  $$\int_{y \in \mathbb{R}} \int_{x \in \mathbb{R}} f(x, y) d x d y$$

  Let $0<a<b$. Show that the function

  $$f(x, y)= \begin{cases}e^{-x y} & \text { if } x \in(0, \infty), y \in[a, b] \\ 0 & \text { otherwise }\end{cases}$$

  is measurable and integrable on $\mathbb{R}^{2}$.

  Evaluate

  $$\int_{0}^{\infty} \frac{e^{-a x}-e^{-b x}}{x} d x$$

  by Fubini's theorem or otherwise.

  comment

Representation Theory

• 4.II.19G

  Representation Theory | Part II, 2005

  (i) State and prove the Weyl integration formula for $S U(2)$.

  (ii) Determine the characters of the symmetric powers of the standard 2-dimensional representation of $S U(2)$ and prove that they are irreducible.

  [Any general theorems from the course may be used.]

  comment

Riemann Surfaces

• 4.II.23H

  Riemann Surfaces | Part II, 2005

  Define what is meant by the degree of a non-constant holomorphic map between compact connected Riemann surfaces, and state the Riemann-Hurwitz formula.

  Let $E_{\Lambda}=\mathbb{C} / \Lambda$ be an elliptic curve defined by some lattice $\Lambda$. Show that the map

  $$\psi: z+\Lambda \in E_{\Lambda} \rightarrow-z+\Lambda \in E_{\Lambda}$$

  is biholomorphic, and that there are four points in $E_{\Lambda}$ fixed by $\psi$.

  Let $S=E_{\Lambda} / \sim$ be the quotient surface (the topological surface obtained by identifying $z+\Lambda$ and $\psi(z+\Lambda)$, for each $z)$ and let $\pi: E_{\Lambda} \rightarrow S$ be the corresponding projection map. Denote by $E_{\Lambda}^{0} \subset E_{\Lambda}$ the complement of the four points fixed by $\psi$, and let $S^{0}=\pi\left(E_{\Lambda}^{0}\right)$. Describe briefly a family of charts making $S^{0}$ into a Riemann surface, so that $\pi: E_{\Lambda}^{0} \rightarrow S^{0}$ is a holomorphic map.

  Now assume that the complex structure of $S^{0}$ extends to $S$, so that $S$ is a Riemann surface, and that the map $\pi$ is in fact holomorphic on all of $E_{\Lambda}$. Calculate the genus of $S$.

  comment

Statistical Modelling

• 4.I.5I

  Statistical Modelling | Part II, 2005

  You see below five $R$ commands, and the corresponding output (which is slightly abbreviated). Without giving any mathematical proofs, explain the purpose of these commands, and interpret the output.

  

  Residual deviance: $1.9369$ on 2 degrees of freedom

  Number of Fisher Scoring iterations: 4

  comment

• 4.II.13I

  Statistical Modelling | Part II, 2005

  (i) Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \beta, \nu\right)=\left(\frac{\nu y_{i}}{\mu_{i}}\right)^{\nu} e^{-y_{i} \nu / \mu_{i}} \frac{1}{\Gamma(\nu)} \frac{1}{y_{i}} \text { for } y_{i}>0$$

  where

  $$1 / \mu_{i}=\beta^{T} x_{i}, \text { for } \quad 1 \leqslant i \leqslant n,$$

  and $x_{1}, \ldots, x_{n}$ are given $p$-dimensional vectors, and $\nu$ is known.

  Show that $\mathbb{E}\left(Y_{i}\right)=\mu_{i}$ and that $\operatorname{var}\left(Y_{i}\right)=\mu_{i}^{2} / \nu$.

  (ii) Find the equation for $\hat{\beta}$, the maximum likelihood estimator of $\beta$, and suggest an iterative scheme for its solution.

  (iii) If $p=2$, and $x_{i}=\left(\begin{array}{c}1 \\ z_{i}\end{array}\right)$, find the large-sample distribution of $\hat{\beta}_{2}$. Write your answer in terms of $a, b, c$ and $\nu$, where $a, b, c$ are defined by

  $$a=\sum \mu_{i}^{2}, \quad b=\sum z_{i} \mu_{i}^{2}, \quad c=\sum z_{i}^{2} \mu_{i}^{2} .$$

  comment

Statistical Physics

• 4.II.34D

  Statistical Physics | Part II, 2005

  Write down an expression for the partition function of a classical particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical particles is placed in the potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. The gas is in equilibrium at temperature $T$. Using a suitable rescaling of variables, show that the free energy $F$ is given by

  $$\frac{F}{N}=-k T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k T+\log I_{n}\right)$$

  where

  $$I_{n}=\left(\frac{2 m \pi}{h^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} e^{-u^{2 n}} d u$$

  Regarding $V$ as an external parameter, find the thermodynamic force $P$, conjugate to $V$, exerted by this system. Find the equation of state and compare with that of an ideal gas confined in a volume $V$.

  Derive expressions for the entropy $S$, the internal energy $E$ and the total heat capacity $C_{V}$ at constant $V$.

  Show that for all $n$ the total heat capacity at constant $P$ is given by

  $$C_{P}=C_{V}+N k$$

  [Note that $\left.\int_{0}^{\infty} u^{2} e^{-u^{2} / 2} d u=\sqrt{\frac{\pi}{2}} .\right]$

  comment

Stochastic Financial Models

• 4.II.28J

  Stochastic Financial Models | Part II, 2005

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be spot price, $K$ be strike price, $T$ be time to maturity, and assume constant interest rate $r$, volatility $\sigma$ and absence of dividends. Write down explicitly the prices of a European call and put,

  $$E C\left(S_{0}, K, \sigma, r, T\right) \text { and } E P\left(S_{0}, K, \sigma, r, T\right)$$

  Use $\Phi$ for the normal distribution function. [No proof is required.]

  (b) From here on assume $r=0$. Keeping $T, \sigma$ fixed, we shorten the notation to $E C\left(S_{0}, K\right)$ and similarly for $E P$. Show that put-call symmetry holds:

  $$E C\left(S_{0}, K\right)=E P\left(K, S_{0}\right)$$

  Check homogeneity: for every real $\alpha>0$

  $$E C\left(\alpha S_{0}, \alpha K\right)=\alpha E C\left(S_{0}, K\right)$$

  (c) Show that the price of a down-and-out European call with strike $K<S_{0}$ and barrier $B \leqslant K$ is given by

  $$E C\left(S_{0}, K\right)-\frac{S_{0}}{B} E C\left(\frac{B^{2}}{S_{0}}, K\right)$$

  (d)

  (i) Specialize the last expression to $B=K$ and simplify.

  (ii) Answer a popular interview question in investment banks: What is the fair value of a down-and-out call given that $S_{0}=100, B=K=80, \sigma=20 \%, r=0, T=1$ ? Identify the corresponding hedge. [It may be helpful to compute Delta first.]

  (iii) Does this hedge work beyond the Black-Scholes model? When does it fail?

  comment

Topics in Analysis

• 4.I.2F

  Topics in Analysis | Part II, 2005

  (i) Let $D \subset \mathbb{C}$ be a domain, let $f: D \rightarrow \mathbb{C}$ be an analytic function and let $z_{0} \in D$. What does Taylor's theorem say about $z_{0}, f$ and $D$ ?

  (ii) Let $K$ be the square consisting of all complex numbers $z$ such that

  $$-1 \leqslant \operatorname{Re}(z) \leqslant 1 \text { and }-1 \leqslant \operatorname{Im}(z) \leqslant 1,$$

  and let $w$ be a complex number not belonging to $K$. Prove that the function $f(z)=$ $(z-w)^{-1}$ can be uniformly approximated on $K$ by polynomials.

  comment

Waves

• 4.II $. 38 \mathrm{E} \quad$

  Waves | Part II, 2005

  Starting from the equations of conservation of mass and momentum for an inviscid compressible fluid, show that for small perturbations about a state of rest and uniform density the velocity is irrotational and the velocity potential satisfies the wave equation. Identify the sound speed $c_{0}$.

  Define the acoustic energy density and acoustic energy flux, and derive the equation for conservation of acoustic energy.

  Show that in any (not necessarily harmonic) acoustic plane wave of wavenumber $\mathbf{k}$ the kinetic and potential energy densities are equal and that the acoustic energy is transported with velocity $c_{0} \widehat{\mathbf{k}}$.

  Calculate the kinetic and potential energy densities for a spherically symmetric outgoing wave. Are they equal?

  comment