Part II, 2005, Paper 2

Algebraic Topology

• 2.II.21H

  Algebraic Topology | Part II, 2005

  State the Van Kampen Theorem. Use this theorem and the fact that $\pi_{1} S^{1}=\mathbb{Z}$ to compute the fundamental groups of the torus $T=S^{1} \times S^{1}$, the punctured torus $T \backslash\{p\}$, for some point $p \in T$, and the connected sum $T \# T$ of two copies of $T$.

  comment

Applications of Quantum Mechanics

• 2.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  Describe briefly the variational approach to the determination of an approximate ground state energy $E_{0}$ of a Hamiltonian $H$.

  Let $\left|\psi_{1}\right\rangle$ and $\left|\psi_{2}\right\rangle$ be two states, and consider the trial state

  $$|\psi\rangle=a_{1}\left|\psi_{1}\right\rangle+a_{2}\left|\psi_{2}\right\rangle$$

  for real constants $a_{1}$ and $a_{2}$. Given that

  $$\begin{aligned} \left\langle\psi_{1} \mid \psi_{1}\right\rangle &=\left\langle\psi_{2} \mid \psi_{2}\right\rangle=1, &\left\langle\psi_{2} \mid \psi_{1}\right\rangle=\left\langle\psi_{1} \mid \psi_{2}\right\rangle=s, \\ \left\langle\psi_{1}|H| \psi_{1}\right\rangle &=\left\langle\psi_{2}|H| \psi_{2}\right\rangle=\mathcal{E}, &\left\langle\psi_{2}|H| \psi_{1}\right\rangle=\left\langle\psi_{1}|H| \psi_{2}\right\rangle=\epsilon, \end{aligned}$$

  and that $\epsilon<s \mathcal{E}$, obtain an upper bound on $E_{0}$ in terms of $\mathcal{E}, \epsilon$ and $s$.

  The normalized ground-state wavefunction of the Hamiltonian

  $$H_{1}=\frac{p^{2}}{2 m}-K \delta(x), \quad K>0,$$

  $$\psi_{1}(x)=\sqrt{\lambda} e^{-\lambda|x|}, \quad \lambda=\frac{m K}{\hbar^{2}} .$$

  Verify that the ground state energy of $H_{1}$ is

  $$E_{B} \equiv\left\langle\psi_{1}|H| \psi_{1}\right\rangle=-\frac{1}{2} K \lambda .$$

  Now consider the Hamiltonian

  $$H=\frac{p^{2}}{2 m}-K \delta(x)-K \delta(x-R)$$

  and let $E_{0}(R)$ be its ground-state energy as a function of $R$. Assuming that

  $$\psi_{2}(x)=\sqrt{\lambda} e^{-\lambda|x-R|},$$

  use $(*)$ to compute $s, \mathcal{E}$ and $\epsilon$ for $\psi_{1}$ and $\psi_{2}$ as given. Hence show that

  $$E_{0}(R) \leqslant E_{B}\left[1+2 \frac{e^{-\lambda R}\left(1+e^{-\lambda R}\right)}{1+(1+\lambda R) e^{-\lambda R}}\right]$$

  Why should you expect this inequality to become an approximate equality for sufficiently large $R$ ? Describe briefly how this is relevant to molecular binding.

  comment

Applied Probability

• 2.II.26I

  Applied Probability | Part II, 2005

  What does it mean to say that $\left(X_{t}\right)$ is a renewal process?

  Let $\left(X_{t}\right)$ be a renewal process with holding times $S_{1}, S_{2}, \ldots$ and let $s>0$. For $n \geqslant 1$, set $T_{n}=S_{X_{s}+n}$. Show that

  $$\mathbb{P}\left(T_{n}>t\right) \geqslant \mathbb{P}\left(S_{n}>t\right), \quad t \geqslant 0,$$

  for all $n$, with equality if $n \geqslant 2$.

  Consider now the case where $S_{1}, S_{2}, \ldots$ are exponential random variables. Show that

  $$\mathbb{P}\left(T_{1}>t\right)>\mathbb{P}\left(S_{1}>t\right), \quad t>0$$

  and that, as $s \rightarrow \infty$,

  $$\mathbb{P}\left(T_{1}>t\right) \rightarrow \mathbb{P}\left(S_{1}+S_{2}>t\right), \quad t \geqslant 0$$

  comment

Classical Dynamics

• 2.I.9C

  Classical Dynamics | Part II, 2005

  A rigid body has principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$ and is moving under the action of no forces with angular velocity components $\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$. Its motion is described by Euler's equations

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}-\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}=0 \\ &I_{2} \dot{\omega}_{2}-\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}=0 \\ &I_{3} \dot{\omega}_{3}-\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}=0 \end{aligned}$$

  Are the components of the angular momentum to be evaluated in the body frame or the space frame?

  Now suppose that an asymmetric body is moving with constant angular velocity $(\Omega, 0,0)$. Show that this motion is stable if and only if $I_{1}$ is the largest or smallest principal moment.

  comment

Coding and Cryptography

• 2.I.4J

  Coding and Cryptography | Part II, 2005

  What is a linear binary code? What is the weight $w(C)$ of a linear binary code $C ?$ Define the bar product $C_{1} \mid C_{2}$ of two binary linear codes $C_{1}$ and $C_{2}$, stating the conditions that $C_{1}$ and $C_{2}$ must satisfy. Under these conditions show that

  $$w\left(C_{1} \mid C_{2}\right) \geqslant \min \left(2 w\left(C_{1}\right), w\left(C_{2}\right)\right)$$

  comment

• 2.II.12J

  Coding and Cryptography | Part II, 2005

  What does it means to say that $f: \mathbb{F}_{2}^{d} \rightarrow \mathbb{F}_{2}^{d}$ is a linear feedback shift register? Let $\left(x_{n}\right)_{n \geqslant 0}$ be a stream produced by such a register. Show that there exist $N, M$ with $N+M \leqslant 2^{d}-1$ such that $x_{r+N}=x_{r}$ for all $r \geqslant M$.

  Explain and justify the Berlekamp-Massey method for 'breaking' a cipher stream arising from a linear feedback register of unknown length.

  Let $x_{n}, y_{n}, z_{n}$ be three streams produced by linear feedback registers. Set

  $$\begin{aligned} &k_{n}=x_{n} \text { if } y_{n}=z_{n} \\ &k_{n}=y_{n} \text { if } y_{n} \neq z_{n} \end{aligned}$$

  Show that $k_{n}$ is also a stream produced by a linear feedback register. Sketch proofs of any theorems that you use.

  comment

Cosmology

• 2.I.10D

  Cosmology | Part II, 2005

  (a) A spherically symmetric star obeys the pressure-support equation

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $P(r)$ is the pressure at a distance $r$ from the centre, $\rho(r)$ is the density, and the mass $m(r)$ is defined through the relation $d m / d r=4 \pi r^{2} \rho(r)$. Multiply $(*)$ by $4 \pi r^{3}$ and integrate over the total volume $V$ of the star to derive the virial theorem

  $$\langle P\rangle V=-\frac{1}{3} E_{\text {grav }}$$

  where $\langle P\rangle$ is the average pressure and $E_{\text {grav }}$ is the total gravitational potential energy.

  (b) Consider a white dwarf supported by electron Fermi degeneracy pressure $P \approx h^{2} n^{5 / 3} / m_{\mathrm{e}}$, where $m_{\mathrm{e}}$ is the electron mass and $n$ is the number density. Assume a uniform density $\rho(r)=m_{\mathrm{p}} n(r) \approx m_{\mathrm{p}}\langle n\rangle$, so the total mass of the star is given by $M=(4 \pi / 3)\langle n\rangle m_{\mathrm{p}} R^{3}$ where $R$ is the star radius and $m_{\mathrm{p}}$ is the proton mass. Show that the total energy of the white dwarf can be written in the form

  $$E_{\mathrm{total}}=E_{\mathrm{kin}}+E_{\mathrm{grav}}=\frac{\alpha}{R^{2}}-\frac{\beta}{R}$$

  where $\alpha, \beta$ are positive constants which you should determine. [You may assume that for an ideal gas $E_{\mathrm{kin}}=\frac{3}{2}\langle P\rangle V$.] Use this expression to explain briefly why a white dwarf is stable.

  comment

• 2.II.15D

  Cosmology | Part II, 2005

  (a) Consider a homogeneous and isotropic universe with scale factor $a(t)$ and filled with mass density $\rho(t)$. Show how the conservation of kinetic energy plus gravitational potential energy for a test particle on the edge of a spherical region in this universe can be used to derive the Friedmann equation

  $$\tag{*} \left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho$$

  where $k$ is a constant. State clearly any assumptions you have made.

  (b) Now suppose that the universe was filled throughout its history with radiation with equation of state $P=\rho c^{2} / 3$. Using the fluid conservation equation and the definition of the relative density $\Omega$, show that the density of this radiation can be expressed as

  $$\rho=\frac{3 H_{0}^{2}}{8 \pi G} \frac{\Omega_{0}}{a^{4}},$$

  where $H_{0}$ is the Hubble parameter today and $\Omega_{0}$ is the relative density today $\left(t=t_{0}\right)$ and $a_{0} \equiv a\left(t_{0}\right)=1$ is assumed. Show also that $k c^{2}=H_{0}^{2}\left(\Omega_{0}-1\right)$ and hence rewrite the Friedmann equation $(*)$ as

  $$\tag{†} \left(\frac{\dot{a}}{a}\right)^{2}=H_{0}^{2} \Omega_{0}\left(\frac{1}{a^{4}}-\frac{\beta}{a^{2}}\right)$$

  where $\beta \equiv\left(\Omega_{0}-1\right) / \Omega_{0}$.

  (c) Now consider a closed model with $k>0$ (or $\Omega>1)$. Rewrite ( $\dagger$ ) using the new time variable $\tau$ defined by

  $$\frac{d t}{d \tau}=a$$

  Hence, or otherwise, solve $(†)$ to find the parametric solution

  $$a(\tau)=\frac{1}{\sqrt{\beta}}(\sin \alpha \tau), \quad t(\tau)=\frac{1}{\alpha \sqrt{\beta}}(1-\cos \alpha \tau),$$

  where $\alpha \equiv H_{0} \sqrt{\left(\Omega_{0}-1\right)} . \quad$ Recall that $\left.\int d x / \sqrt{1-x^{2}}=\sin ^{-1} x .\right]$

  Using the solution for $a(\tau)$, find the value of the new time variable $\tau=\tau_{0}$ today and hence deduce that the age of the universe in this model is

  $$t_{0}=H_{0}^{-1} \frac{\sqrt{\Omega_{0}}-1}{\Omega_{0}-1}$$

  comment

Differential Geometry

• 2.II.24H

  Differential Geometry | Part II, 2005

  State the isoperimetric inequality in the plane.

  Let $S \subset \mathbb{R}^{3}$ be a surface. Let $p \in S$ and let $S_{r}(p)$ be a geodesic circle of centre $p$ and radius $r$ ( $r$ small). Let $L$ be the length of $S_{r}(p)$ and $A$ be the area of the region bounded by $S_{r}(p)$. Prove that

  $$4 \pi A-L^{2}=\pi^{2} r^{4} K(p)+\varepsilon(r),$$

  where $K(p)$ is the Gaussian curvature of $S$ at $p$ and

  $$\lim _{r \rightarrow 0} \frac{\varepsilon(r)}{r^{4}}=0 .$$

  When $K(p)>0$ and $r$ is small, compare this briefly with the isoperimetric inequality in the plane.

  comment

Dynamical Systems

• 2.I.7B

  Dynamical Systems | Part II, 2005

  Define Lyapunov stability and quasi-asymptotic stability of a fixed point $\mathbf{x}_{0}$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$.

  By considering a Lyapunov function of the form $V=g(x)+y^{2}$, show that the origin is an asymptotically stable fixed point of

  $$\begin{aligned} &\dot{x}=-y-x^{3} \\ &\dot{y}=x^{5} \end{aligned}$$

  [Lyapunov's Second Theorem may be used without proof, provided you show that its conditions apply.]

  comment

• 2.II.14B

  Dynamical Systems | Part II, 2005

  Prove that if a continuous map $F$ of an interval into itself has a periodic orbit of period three then it also has periodic orbits of least period $n$ for all positive integers $n$.

  Explain briefly why there must be at least two periodic orbits of least period $5 .$

  [You may assume without proof:

  (i) If $U$ and $V$ are non-empty closed bounded intervals such that $V \subseteq F(U)$ then there is a closed bounded interval $K \subseteq U$ such that $F(K)=V$.

  (ii) The Intermediate Value Theorem.]

  comment

Fluid Dynamics II

• 2.II.36E

  Fluid Dynamics II | Part II, 2005

  A volume $V$ of very viscous fluid of density $\rho$ and dynamic viscosity $\mu$ is released at the origin on a rigid horizontal boundary at time $t=0$. Using lubrication theory, determine the velocity profile in the gravity current once it has spread sufficiently that the axisymmetric thickness $h(r, t)$ of the current is much less than the radius $R(t)$ of the front.

  Derive the differential equation

  $$\frac{\partial h}{\partial t}=\frac{\beta}{r} \frac{\partial}{\partial r}\left(r h^{3} \frac{\partial h}{\partial r}\right)$$

  where $\beta$ is to be determined.

  Write down the other equations that are needed to determine the appropriate similarity solution for this problem.

  Determine the similarity solution and calculate $R(t)$.

  comment

Further Complex Methods

• 2.I.8A

  Further Complex Methods | Part II, 2005

  The Hankel representation of the gamma function is

  $$\Gamma(z)=\frac{1}{2 i \sin (\pi z)} \int_{-\infty}^{\left(0^{+}\right)} t^{z-1} e^{t} d t$$

  where the path of integration is the Hankel contour.

  Use this representation to find the residue of $\Gamma(z)$ at $z=-n$, where $n$ is a nonnegative integer.

  Is there a pole at $z=n$, where $n$ is a positive integer? Justify your answer carefully, working only from the above representation of $\Gamma(z)$.

  comment

Galois Theory

• 2.II.18G

  Galois Theory | Part II, 2005

  Let $K$ be a field of characteristic 0 containing all roots of unity.

  (i) Let $L$ be the splitting field of the polynomial $X^{n}-a$ where $a \in K$. Show that the Galois group of $L / K$ is cyclic.

  (ii) Suppose that $M / K$ is a cyclic extension of degree $m$ over $K$. Let $g$ be a generator of the Galois group and $\zeta \in K$ a primitive $m$-th root of 1 . By considering the resolvent

  $$R(w)=\sum_{i=0}^{m-1} \frac{g^{i}(w)}{\zeta^{i}}$$

  of elements $w \in M$, show that $M$ is the splitting field of a polynomial $X^{m}-a$ for some $a \in K$.

  comment

General Relativity

• 2.II.35C

  General Relativity | Part II, 2005

  State without proof the properties of local inertial coordinates $x^{a}$ centred on an arbitrary spacetime event $p$. Explain their physical significance.

  Obtain an expression for $\partial_{a} \Gamma_{b}{ }^{c}$ at $p$ in inertial coordinates. Use it to derive the formula

  $$R_{a b c d}=\frac{1}{2}\left(\partial_{b} \partial_{c} g_{a d}+\partial_{a} \partial_{d} g_{b c}-\partial_{b} \partial_{d} g_{a c}-\partial_{a} \partial_{c} g_{b d}\right)$$

  for the components of the Riemann tensor at $p$ in local inertial coordinates. Hence deduce that at any point in any chart $R_{a b c d}=R_{c d a b}$.

  Consider the metric

  $$d s^{2}=\frac{\eta_{a b} d x^{a} d x^{b}}{\left(1+L^{-2} \eta_{a b} x^{a} x^{b}\right)^{2}}$$

  where $\eta_{a b}=\operatorname{diag}(1,1,1,-1)$ is the Minkowski metric tensor and $L$ is a constant. Compute the Ricci scalar $R=R_{a b}^{a b}$ at the origin $x^{a}=0$.

  comment

Geometry of Group Actions

• 2.I.3G

  Geometry of Group Actions | Part II, 2005

  Describe the geodesics in the disc model of the hyperbolic plane $\mathbb{H}^{2}$.

  Define the area of a region in $\mathbb{H}^{2}$. Compute the area $A(r)$ of a hyperbolic circle of radius $r$ from the definition just given. Compute the circumference $C(r)$ of a hyperbolic circle of radius $r$, and check explicitly that $d A(r) / d r=C(r)$.

  How could you define $\pi$ geometrically if you lived in $\mathbb{H}^{2}$ ? Briefly justify your answer.

  comment

Graph Theory

• 2.II.17F

  Graph Theory | Part II, 2005

  Brooks' Theorem states that if $G$ is a connected graph then $\chi(G) \leqslant \Delta(G)$ unless $G$ is complete or is an odd cycle. Prove the theorem for 3-connected graphs $G$.

  Let $G$ be a graph, and let $d_{1}+d_{2}=\Delta(G)-1$. By considering a partition $V_{1}, V_{2}$ of $V(G)$ that minimizes the quantity $d_{2} e\left(G\left[V_{1}\right]\right)+d_{1} e\left(G\left[V_{2}\right]\right)$, show that there is a partition with $\Delta\left(G\left[V_{i}\right]\right) \leqslant d_{i}, i=1,2$.

  By taking $d_{1}=3$, show that if a graph $G$ contains no $K_{4}$ then $\chi(G) \leqslant \frac{3}{4} \Delta(G)+\frac{3}{2}$.

  comment

Integrable Systems

• 2.II.31C

  Integrable Systems | Part II, 2005

  Suppose $q(x, t)$ satisfies the $m K d V$ equation

  $$q_{t}+q_{x x x}+6 q^{2} q_{x}=0$$

  where $q_{t}=\partial q / \partial t$ etc.

  (a) Find the 1-soliton solution.

  [You may use, without proof, the indefinite integral $\int \frac{d x}{x \sqrt{1-x^{2}}}=-\operatorname{arcsech} x$.]

  (b) Express the self-similar solution of the $\mathrm{KKdV}$ equation in terms of a solution, denoted by $v(z)$, of the Painlevé II equation.

  (c) Using the Ansatz

  $$\frac{d v}{d z}+i v^{2}-\frac{i}{6} z=0$$

  find a particular solution of the mKdV equation in terms of a solution of the Airy equation

  $$\frac{d^{2} \Psi}{d z^{2}}+\frac{z}{6} \Psi=0$$

  comment

Linear Analysis

• 2.II.22F

  Linear Analysis | Part II, 2005

  Let $X$ and $Y$ be Banach spaces. Define what it means for a linear operator $T: X \rightarrow Y$ to be compact. For a linear operator $T: X \rightarrow X$, define the spectrum, point spectrum, and resolvent set of $T$.

  Now let $H$ be a complex Hilbert space. Define what it means for a linear operator $T: H \rightarrow H$ to be self-adjoint. Suppose $e_{1}, e_{2}, \ldots$ is an orthonormal basis for $H$. Define a linear operator $T: H \rightarrow H$ by setting $T e_{i}=\frac{1}{i} e_{i}$. Is $T$ compact? Is $T$ self-adjoint? Justify your answers. Describe, with proof, the spectrum, point spectrum, and resolvent set of $T$.

  comment

Logic and Set Theory

• 2.II.16F

  Logic and Set Theory | Part II, 2005

  Give the inductive and the synthetic definitions of ordinal addition, and prove that they are equivalent. Give an example to show that ordinal addition is not commutative.

  Which of the following assertions about ordinals $\alpha, \beta$ and $\gamma$ are always true, and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha+(\beta+\gamma)=(\alpha+\beta)+\gamma$.

  (ii) If $\alpha$ and $\beta$ are limit ordinals then $\alpha+\beta=\beta+\alpha$.

  (iii) If $\alpha+\beta=\omega_{1}$ then $\alpha=0$ or $\alpha=\omega_{1}$.

  (iv) If $\alpha+\beta=\omega_{1}$ then $\beta=0$ or $\beta=\omega_{1}$.

  comment

Mathematical Biology

• 2.I.6E

  Mathematical Biology | Part II, 2005

  Consider a system with stochastic reaction events

  $$x \stackrel{\lambda}{\longrightarrow} x+1 \quad \text { and } \quad x \stackrel{\beta x^{2}}{\longrightarrow} x-2,$$

  where $\lambda$ and $\beta$ are rate constants.

  (a) State or derive the exact differential equation satisfied by the average number of molecules $<x>$. Assuming that fluctuations are negligible, approximate the differential equation to obtain the steady-state value of $\langle x\rangle$.

  (b) Using this approximation, calculate the elasticity $H$, the average lifetime $\tau$, and the average chemical event size $<r>$ (averaged over fluxes).

  (c) State the stationary Fluctuation Dissipation Theorem for the normalised variance $\eta$. Hence show that

  $$\eta=\frac{3}{4<x>} .$$

  comment

• 2.II.13E

  Mathematical Biology | Part II, 2005

  Consider the reaction-diffusion system

  $$\begin{aligned} &\frac{\partial u}{\partial \tau}=\beta_{u}\left(\frac{u^{2}}{v}-u\right)+D_{u} \frac{\partial^{2} u}{\partial x^{2}} \\ &\frac{\partial v}{\partial \tau}=\beta_{v}\left(u^{2}-v\right)+D_{v} \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  for an activator $u$ and inhibitor $v$, where $\beta_{u}$ and $\beta_{v}$ are degradation rate constants and $D_{u}$ and $D_{v}$ are diffusion rate constants.

  (a) Find a suitably scaled time $t$ and length $s$ such that

  $$\begin{aligned} \frac{\partial u}{\partial t} &=\frac{u^{2}}{v}-u+\frac{\partial^{2} u}{\partial s^{2}} \\ \frac{1}{Q} \frac{\partial v}{\partial t} &=u^{2}-v+P \frac{\partial^{2} v}{\partial s^{2}} \end{aligned}$$

  and find expressions for $P$ and $Q$.

  (b) Show that the Jacobian matrix for small spatially homogenous deviations from a nonzero steady state of $(*)$ is

  $$J=\left(\begin{array}{cc} 1 & -1 \\ 2 Q & -Q \end{array}\right)$$

  and find the values of $Q$ for which the steady state is stable.

  [Hint: The eigenvalues of a $2 \times 2$ real matrix both have positive real parts iff the matrix has a positive trace and determinant.]

  (c) Derive linearised ordinary differential equations for the amplitudes $\hat{u}(t)$ and $\hat{v}(t)$ of small spatially inhomogeneous deviations from a steady state of $(*)$ that are proportional to $\cos (s / L)$, where $L$ is a constant.

  (d) Assuming that the system is stable to homogeneous perturbations, derive the condition for inhomogeneous instability. Interpret this condition in terms of how far activator and inhibitor molecules diffuse on average before they are degraded.

  (e) Calculate the lengthscale $L_{\text {crit }}$ of disturbances that are expected to be observed when the condition for inhomogeneous instability is just satisfied. What are the dominant mechanisms for stabilising disturbances on lengthscales (i) much less than and (ii) much greater than $L_{\text {crit }}$ ?

  comment

Number Fields

• 2.II.20G

  Number Fields | Part II, 2005

  Show that $\varepsilon=(3+\sqrt{7}) /(3-\sqrt{7})$ is a unit in $k=\mathbb{Q}(\sqrt{7})$. Show further that 2 is the square of the principal ideal in $k$ generated by $3+\sqrt{7}$.

  Assuming that the Minkowski constant for $k$ is $\frac{1}{2}$, deduce that $k$ has class number 1 .

  Assuming further that $\varepsilon$ is the fundamental unit in $k$, show that the complete solution in integers $x, y$ of the equation $x^{2}-7 y^{2}=2$ is given by

  $$x+\sqrt{7} y=\pm \varepsilon^{n}(3+\sqrt{7}) \quad(n=0, \pm 1, \pm 2, \ldots) .$$

  Calculate the particular solution in positive integers $x, y$ when $n=1$

  comment

Number Theory

• 2.I.1H

  Number Theory | Part II, 2005

  Recall that, if $p$ is an odd prime, a primitive root modulo $p$ is a generator of the cyclic (multiplicative) group $(\mathbb{Z} / p \mathbb{Z})^{\times}$. Let $p$ be an odd prime of the form $2^{2^{n}}+1$; show that $a$ is a primitive root $\bmod p$ if and only if $a$ is not a quadratic residue mod $p$. Use this result to prove that 7 is a primitive root modulo every such prime.

  comment

Numerical Analysis

• 2.II.38A

  Numerical Analysis | Part II, 2005

  Define a Krylov subspace $\mathcal{K}_{n}(A, v)$.

  Let $d_{n}$ be the dimension of $\mathcal{K}_{n}(A, v)$. Prove that the sequence $\left\{d_{m}\right\}_{m=1,2, . .}$ increases monotonically. Show that, moreover, there exists an integer $k$ with the following property: $d_{m}=m$ for $m=1,2, \ldots, k$, while $d_{m}=k$ for $m \geqslant k$. Assuming that $A$ has a full set of eigenvectors, show that $k$ is equal to the number of eigenvectors of $A$ required to represent the vector $v$.

  comment

Optimization and Control

• 2.II.29I

  Optimization and Control | Part II, 2005

  Explain what is meant by a time-homogeneous discrete time Markov decision problem.

  What is the positive programming case?

  A discrete time Markov decision problem has state space $\{0,1, \ldots, N\}$. In state $i, i \neq 0, N$, two actions are possible. We may either stop and obtain a terminal reward $r(i) \geqslant 0$, or may continue, in which case the subsequent state is equally likely to be $i-1$ or $i+1$. In states 0 and $N$ stopping is automatic (with terminal rewards $r(0)$ and $r(N)$ respectively). Starting in state $i$, denote by $V_{n}(i)$ and $V(i)$ the maximal expected terminal reward that can be obtained over the first $n$ steps and over the infinite horizon, respectively. Prove that $\lim _{n \rightarrow \infty} V_{n}=V$.

  Prove that $V$ is the smallest concave function such that $V(i) \geqslant r(i)$ for all $i$.

  Describe an optimal policy.

  Suppose $r(0), \ldots, r(N)$ are distinct numbers. Show that the optimal policy is unique, or give a counter-example.

  comment

Partial Differential Equations

• 2.II.30C

  Partial Differential Equations | Part II, 2005

  Define a fundamental solution of a linear partial differential operator $P$. Prove that the function

  $$G(x)=\frac{1}{2} e^{-|x|}$$

  defines a distribution which is a fundamental solution of the operator $P$ given by

  $$P u=-\frac{d^{2} u}{d x^{2}}+u .$$

  Hence find a solution $u_{0}$ to the equation

  $$-\frac{d^{2} u_{0}}{d x^{2}}+u_{0}=V(x),$$

  where $V(x)=0$ for $|x|>1$ and $V(x)=1$ for $|x| \leqslant 1$.

  Consider the functional

  $$I[u]=\int_{\mathbb{R}}\left\{\frac{1}{2}\left[\left(\frac{d u}{d x}\right)^{2}+u^{2}\right]-V u\right\} d x .$$

  Show that $I\left[u_{0}+\phi\right]>I\left[u_{0}\right]$ for all Schwartz functions $\phi$ that are not identically zero.

  comment

Principles of Quantum Mechanics

• 2.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  The components of $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ are $2 \times 2$ hermitian matrices obeying

  $$\left[\sigma_{i}, \sigma_{j}\right]=2 i \varepsilon_{i j k} \sigma_{k} \quad \text { and } \quad(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=1$$

  for any unit vector $\mathbf{n}$. Show that these properties imply

  $$(\mathbf{a} \cdot \boldsymbol{\sigma})(\mathbf{b} \cdot \boldsymbol{\sigma})=\mathbf{a} \cdot \mathbf{b}+i(\mathbf{a} \times \mathbf{b}) \cdot \boldsymbol{\sigma}$$

  for any constant vectors a and $\mathbf{b}$. Assuming that $\theta$ is real, explain why the matrix $U=\exp (-i \mathbf{n} \cdot \boldsymbol{\sigma} \theta / 2)$ is unitary, and show that

  $$U=\cos (\theta / 2)-i \mathbf{n} \cdot \boldsymbol{\sigma} \sin (\theta / 2)$$

  Hence deduce that

  $$U \mathbf{m} \cdot \boldsymbol{\sigma} U^{-1}=\mathbf{m} \cdot \boldsymbol{\sigma} \cos \theta+(\mathbf{n} \times \mathbf{m}) \cdot \boldsymbol{\sigma} \sin \theta$$

  where $\mathbf{m}$ is any unit vector orthogonal to $\mathbf{n}$.

  Write down an equation relating the matrices $\sigma$ and the angular momentum operator $\mathbf{S}$ for a particle of spin one half, and explain briefly the significance of the conditions $(*)$. Show that if $|\chi\rangle$ is a state with spin 'up' measured along the direction $(0,0,1)$ then, for a certain choice of $\mathbf{n}, U|\chi\rangle$ is a state with spin 'up' measured along the direction $(\sin \theta, 0, \cos \theta)$.

  comment

Principles of Statistics

• 2.II.27I

  Principles of Statistics | Part II, 2005

  (i) Suppose that $X$ is a multivariate normal vector with mean $\mu \in \mathbb{R}^{d}$ and covariance matrix $\sigma^{2} I$, where $\mu$ and $\sigma^{2}$ are both unknown, and $I$ denotes the $d \times d$ identity matrix. Suppose that $\Theta_{0} \subset \Theta_{1}$ are linear subspaces of $\mathbb{R}^{d}$ of dimensions $d_{0}$ and $d_{1}$, where $d_{0}<d_{1}<d$. Let $P_{i}$ denote orthogonal projection onto $\Theta_{i}(i=0,1)$. Carefully derive the joint distribution of $\left(\left|X-P_{1} X\right|^{2},\left|P_{1} X-P_{0} X\right|^{2}\right)$ under the hypothesis $H_{0}: \mu \in \Theta_{0}$. How could you use this to make a test of $H_{0}$ against $H_{1}: \mu \in \Theta_{1}$ ?

  (ii) Suppose that $I$ students take $J$ exams, and that the mark $X_{i j}$ of student $i$ in exam $j$ is modelled as

  $$X_{i j}=m+\alpha_{i}+\beta_{j}+\varepsilon_{i j}$$

  where $\sum_{i} \alpha_{i}=0=\sum_{j} \beta_{j}$, the $\varepsilon_{i j}$ are independent $N\left(0, \sigma^{2}\right)$, and the parameters $m, \alpha, \beta$ and $\sigma$ are unknown. Construct a test of $H_{0}: \beta_{j}=0$ for all $j$ against $H_{1}: \sum_{j} \beta_{j}=0$.

  comment

Probability and Measure

• 2.II.25J

  Probability and Measure | Part II, 2005

  Let $\mathcal{R}$ be a family of random variables on the common probability space $(\Omega, \mathcal{F}, \mathbb{P})$. What is meant by saying that $\mathcal{R}$ is uniformly integrable? Explain the use of uniform integrability in the study of convergence in probability and in $L^{1}$. [Clear definitions should be given of any terms used, but proofs may be omitted.]

  Let $\mathcal{R}_{1}$ and $\mathcal{R}_{2}$ be uniformly integrable families of random variables on $(\Omega, \mathcal{F}, \mathbb{P})$. Show that the family $\mathcal{R}$ given by

  $$\mathcal{R}=\left\{X+Y: X \in \mathcal{R}_{1}, Y \in \mathcal{R}_{2}\right\}$$

  is uniformly integrable.

  comment

Representation Theory

• 2.II.19G

  Representation Theory | Part II, 2005

  Let $G$ be a finite group and $\left\{\chi_{i}\right\}$ the set of its irreducible characters. Also choose representatives $g_{j}$ for the conjugacy classes, and denote by $Z\left(g_{j}\right)$ their centralisers.

  (i) State the orthogonality and completeness relations for the $\chi_{k}$.

  (ii) Using Part (i), or otherwise, show that

  $$\sum_{i} \overline{\chi_{i}\left(g_{j}\right)} \cdot \chi_{i}\left(g_{k}\right)=\delta_{j k} \cdot\left|Z\left(g_{j}\right)\right|$$

  (iii) Let $A$ be the matrix with $A_{i j}=\chi_{i}\left(g_{j}\right)$. Prove that

  $$|\operatorname{det} A|^{2}=\prod_{j}\left|Z\left(g_{j}\right)\right|$$

  (iv) Show that $\operatorname{det} A$ is either real or purely imaginary, explaining when each situation occurs.

  [Hint for (iv): Consider the effect of complex conjugation on the rows of the matrix A.]

  comment

Riemann Surfaces

• 2.II.23H

  Riemann Surfaces | Part II, 2005

  Define the terms function element and complete analytic function.

  Let $(f, D)$ be a function element such that $f(z)^{n}=p(z)$, for some integer $n \geqslant 2$, where $p(z)$ is a complex polynomial with no multiple roots. Let $F$ be the complete analytic function containing $(f, D)$. Show that every function element $(\tilde{f}, \tilde{D})$ in $F$ satisfies $\tilde{f}(z)^{n}=p(z) .$

  Describe how the non-singular complex algebraic curve

  $$C=\left\{(z, w) \in \mathbb{C}^{2} \mid w^{n}-p(z)=0\right\}$$

  can be made into a Riemann surface such that the first and second projections $\mathbb{C}^{2} \rightarrow \mathbb{C}$ define, by restriction, holomorphic maps $f_{1}, f_{2}: C \rightarrow \mathbb{C}$.

  Explain briefly the relation between $C$ and the Riemann surface $S(F)$ for the complete analytic function $F$ given earlier.

  [You do not need to prove the Inverse Function Theorem, provided that you state it accurately.]

  comment

Statistical Modelling

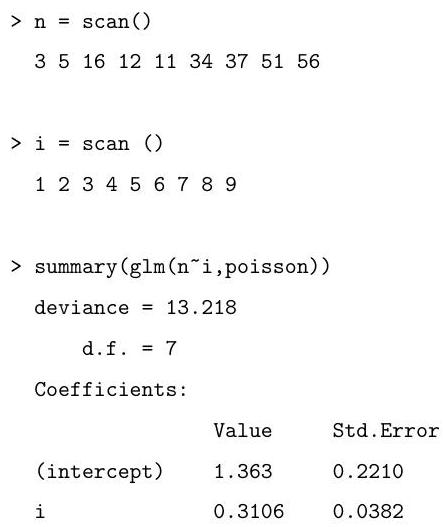
• 2.I.5I

  Statistical Modelling | Part II, 2005

  You see below three $R$ commands, and the corresponding output (which is slightly abbreviated). Explain the effects of the commands. How is the deviance defined, and why do we have d.f. $=7$ in this case? Interpret the numerical values found in the output.

  

  comment

Statistical Physics

• 2.II.34D

  Statistical Physics | Part II, 2005

  Write down the first law of thermodynamics in differential form applied to an infinitesimal reversible change.

  Explain what is meant by an adiabatic change.

  Starting with the first law in differential form, derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  Hence show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=T\left(\frac{\partial P}{\partial T}\right)_{V}-P$$

  For radiation in thermal equilibrium at temperature $T$ in volume $V$, it is given that $E=V e(T)$ and $P=e(T) / 3$. Hence deduce Stefan's Law,

  $$E=a V T^{4}$$

  where $a$ is a constant.

  The radiation is allowed to expand adiabatically. Show that $V T^{3}$ is constant during the expansion.

  comment

Stochastic Financial Models

• 2.II.28J

  Stochastic Financial Models | Part II, 2005

  (i) At the beginning of year $n$, an investor makes decisions about his investment and consumption for the coming year. He first takes out an amount $c_{n}$ from his current wealth $w_{n}$, and sets this aside for consumption. He splits his remaining wealth between a bank account (unit wealth invested at the start of the year will have grown to a sure amount $r>1$ by the end of the year), and the stock market. Unit wealth invested in the stock market will have become the random amount $X_{n+1}>0$ by the end of the year.

  The investor's objective is to invest and consume so as to maximise the expected value of $\sum_{n=1}^{N} U\left(c_{n}\right)$, where $U$ is strictly increasing and strictly convex. Consider the dynamic programming equation (Bellman equation) for his problem,

  $$\begin{aligned} V_{n}(w) &=\sup _{c, \theta}\left\{U(c)+E_{n}\left[V_{n+1}\left(\theta(w-c) X_{n+1}+(1-\theta)(w-c) r\right)\right]\right\} \quad(0 \leqslant n<N), \\ V_{N}(w) &=U(w) . \end{aligned}$$

  Explain all undefined notation, and explain briefly why the equation holds.

  (ii) Supposing that the $X_{i}$ are independent and identically distributed, and that $U(x)=x^{1-R} /(1-R)$, where $R>0$ is different from 1 , find as explicitly as you can the form of the agent's optimal policy.

  (iii) Return to the general problem of (i). Assuming that the sample space $\Omega$ is finite, and that all suprema are attained, show that

  $$\begin{aligned} E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\left(X_{n+1}-r\right)\right] &=0 \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=U^{\prime}\left(c_{n}^{*}\right) \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=V_{n}^{\prime}\left(w_{n}^{*}\right) \end{aligned}$$

  where $\left(c_{n}^{*}, w_{n}^{*}\right)_{0 \leqslant n \leqslant N}$ denotes the optimal consumption and wealth process for the problem. Explain the significance of each of these equalities.

  comment

Topics in Analysis

• 2.II.11F

  Topics in Analysis | Part II, 2005

  (i) State the Baire category theorem. Deduce from it a statement about nowhere dense sets.

  (ii) Let $X$ be the set of all real numbers with decimal expansions consisting of the digits 4 and 5 only. Prove that there is a real number $t$ that cannot be written in the form $x+y$ with $x \in X$ and $y$ rational.

  comment

Waves

• 2.II.37E

  Waves | Part II, 2005

  Show that, in the standard notation for a one-dimensional flow of a perfect gas at constant entropy, the quantity $u+2\left(c-c_{0}\right) /(\gamma-1)$ remains constant along characteristics $d x / d t=u+c$.

  A perfect gas is initially at rest and occupies a tube in $x>0$. A piston is pushed into the gas so that its position at time $t$ is $x(t)=\frac{1}{2} f t^{2}$, where $f>0$ is a constant. Find the time and position at which a shock first forms in the gas.

  comment