For real $s \geqslant 0$ and $F \subset \mathbb{R}^{n}$, give a careful definition of the $s$-dimensional Hausdorff measure of $F$ and of the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of $F$.

For $1 \leqslant i \leqslant k$, suppose $S_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is a similarity with contraction factor $c_{i} \in(0,1)$. Prove there is a unique non-empty compact invariant set $I$ for the $\left\{S_{i}\right\}$. State a formula for the Hausdorff dimension of $I$, under an assumption on the $S_{i}$ you should state.

Hence show the Hausdorff dimension of the fractal $F$ given by iterating the scheme below (at each stage replacing each edge by a new copy of the generating template) is $\operatorname{dim}_{H}(F)=3 / 2$.

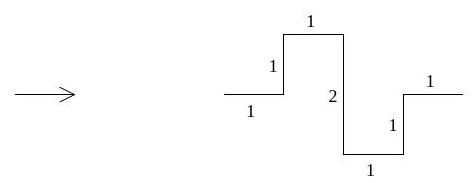
[Numbers denote lengths]