(a) Define the cross-ratio [z1,z2,z3,z4] of four distinct points z1,z2,z3,z4∈C∪{∞}. Show that the cross-ratio is invariant under Möbius transformations. Express [z2,z1,z3,z4] in terms of [z1,z2,z3,z4].
(b) Show that [z1,z2,z3,z4] is real if and only if z1,z2,z3,z4 lie on a line or circle in C∪{∞}.
(c) Let z1,z2,z3,z4 lie on a circle in C, given in anti-clockwise order as depicted.
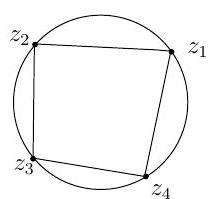
Show that [z1,z2,z3,z4] is a negative real number, and that [z2,z1,z3,z4] is a positive real number greater than 1 . Show that ∣[z1,z2,z3,z4]∣+1=∣[z2,z1,z3,z4]∣. Use this to deduce Ptolemy's relation on lengths of edges and diagonals of the inscribed 4-gon:
∣z1−z3∣∣z2−z4∣=∣z1−z2∣∣z3−z4∣+∣z2−z3∣∣z4−z1∣
