Part IB, 2005, Paper 4

Analysis II

• 4.I 3 B

  Analysis II | Part IB, 2005

  Let $V$ be the vector space of continuous real-valued functions on $[0,1]$. Show that the function

  $$\|f\|=\int_{0}^{1}|f(x)| d x$$

  defines a norm on $V$.

  For $n=1,2, \ldots$, let $f_{n}(x)=e^{-n x}$. Is $f_{n}$ a convergent sequence in the space $V$ with this norm? Justify your answer.

  comment

• 4.II.13B

  Analysis II | Part IB, 2005

  Let $F:[-a, a] \times\left[x_{0}-r, x_{0}+r\right] \rightarrow \mathbf{R}$ be a continuous function. Let $C$ be the maximum value of $|F(t, x)|$. Suppose there is a constant $K$ such that

  $$|F(t, x)-F(t, y)| \leqslant K|x-y|$$

  for all $t \in[-a, a]$ and $x, y \in\left[x_{0}-r, x_{0}+r\right]$. Let $b<\min (a, r / C, 1 / K)$. Show that there is a unique $C^{1}$ function $x:[-b, b] \rightarrow\left[x_{0}-r, x_{0}+r\right]$ such that

  $$x(0)=x_{0}$$

  and

  $$\frac{d x}{d t}=F(t, x(t)) .$$

  [Hint: First show that the differential equation with its initial condition is equivalent to the integral equation

  $$\left.x(t)=x_{0}+\int_{0}^{t} F(s, x(s)) d s .\right]$$

  comment

Complex Analysis

• 4.I.4A

  Complex Analysis | Part IB, 2005

  Let $\gamma:[0,1] \rightarrow \mathbf{C}$ be a closed path, where all paths are assumed to be piecewise continuously differentiable, and let $a$ be a complex number not in the image of $\gamma$. Write down an expression for the winding number $n(\gamma, a)$ in terms of a contour integral. From this characterization of the winding number, prove the following properties:

  (a) If $\gamma_{1}$ and $\gamma_{2}$ are closed paths not passing through zero, and if $\gamma:[0,1] \rightarrow \mathbf{C}$ is defined by $\gamma(t)=\gamma_{1}(t) \gamma_{2}(t)$ for all $t$, then

  $$n(\gamma, 0)=n\left(\gamma_{1}, 0\right)+n\left(\gamma_{2}, 0\right)$$

  (b) If $\eta:[0,1] \rightarrow \mathbf{C}$ is a closed path whose image is contained in $\{\operatorname{Re}(z)>0\}$, then $n(\eta, 0)=0$.

  (c) If $\gamma_{1}$ and $\gamma_{2}$ are closed paths and $a$ is a complex number, not in the image of either path, such that

  $$\left|\gamma_{1}(t)-\gamma_{2}(t)\right|<\left|\gamma_{1}(t)-a\right|$$

  for all $t$, then $n\left(\gamma_{1}, a\right)=n\left(\gamma_{2}, a\right)$.

  [You may wish here to consider the path defined by $\eta(t)=1-\left(\gamma_{1}(t)-\gamma_{2}(t)\right) /\left(\gamma_{1}(t)-a\right)$.]

  comment

Complex Methods

• 4.II.15F

  Complex Methods | Part IB, 2005

  Determine the Fourier expansion of the function $f(x)=\sin \lambda x$, where $-\pi \leqslant x \leqslant \pi$, in the two cases where $\lambda$ is an integer and $\lambda$ is a real non-integer.

  Using the Parseval identity in the case $\lambda=\frac{1}{2}$, find an explicit expression for the sum

  $$\sum_{n=1}^{\infty} \frac{n^{2}}{\left(4 n^{2}-1\right)^{2}}$$

  comment

Electromagnetism

• 4.I.7H

  Electromagnetism | Part IB, 2005

  For a static current density $\mathbf{J}(\mathbf{x})$ show that we may choose the vector potential $\mathbf{A}(\mathbf{x})$ so that

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J} .$$

  For a loop $L$, centred at the origin, carrying a current $I$ show that

  $$\mathbf{A}(\mathbf{x})=\frac{\mu_{0} I}{4 \pi} \oint_{L} \frac{1}{|\mathbf{x}-\mathbf{r}|} \mathrm{d} \mathbf{r} \sim-\frac{\mu_{0} I}{4 \pi} \frac{1}{|\mathbf{x}|^{3}} \oint_{L} \frac{1}{2} \mathbf{x} \times(\mathbf{r} \times \mathrm{d} \mathbf{r}) \quad \text { as } \quad|\mathbf{x}| \rightarrow \infty$$

  [You may assume

  $$-\nabla^{2} \frac{1}{4 \pi|\mathbf{x}|}=\delta^{3}(\mathbf{x})$$

  and for fixed vectors $\mathbf{a}, \mathbf{b}$

  $$\left.\oint_{L} \mathbf{a} \cdot \mathrm{d} \mathbf{r}=0, \quad \oint_{L}(\mathbf{a} \cdot \mathbf{r} \mathbf{b} \cdot \mathrm{d} \mathbf{r}+\mathbf{b} \cdot \mathbf{r} \mathbf{a} \cdot \mathrm{d} \mathbf{r})=0 .\right]$$

  comment

Fluid Dynamics

• 4.II.18E

  Fluid Dynamics | Part IB, 2005

  A fluid of density $\rho_{1}$ occupies the region $z>0$ and a second fluid of density $\rho_{2}$ occupies the region $z<0$. State the equations and boundary conditions that are satisfied by the corresponding velocity potentials $\phi_{1}$ and $\phi_{2}$ and pressures $p_{1}$ and $p_{2}$ when the system is perturbed so that the interface is at $z=\zeta(x, t)$ and the motion is irrotational.

  Seek a set of linearised equations and boundary conditions when the disturbances are proportional to $e^{i(k x-\omega t)}$, and derive the dispersion relation

  $$\omega^{2}=\frac{\rho_{2}-\rho_{1}}{\rho_{2}+\rho_{1}} g k,$$

  where $g$ is the gravitational acceleration.

  comment

Geometry

• 4.II.12A

  Geometry | Part IB, 2005

  Given a parametrized smooth embedded surface $\sigma: V \rightarrow U \subset \mathbf{R}^{3}$, where $V$ is an open subset of $\mathbf{R}^{2}$ with coordinates $(u, v)$, and a point $P \in U$, define what is meant by the tangent space at $P$, the unit normal $\mathbf{N}$ at $P$, and the first fundamental form

  $$E d u^{2}+2 F d u d v+G d v^{2} .$$

  [You need not show that your definitions are independent of the parametrization.]

  The second fundamental form is defined to be

  $$L d u^{2}+2 M d u d v+N d v^{2},$$

  where $L=\sigma_{u u} \cdot \mathbf{N}, M=\sigma_{u v} \cdot \mathbf{N}$ and $N=\sigma_{v v} \cdot \mathbf{N}$. Prove that the partial derivatives of $\mathbf{N}$ (considered as a vector-valued function of $u, v$ ) are of the form $\mathbf{N}_{u}=a \sigma_{u}+b \sigma_{v}$, $\mathbf{N}_{v}=c \sigma_{u}+d \sigma_{v}$, where

  $$-\left(\begin{array}{cc} L & M \\ M & N \end{array}\right)=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right)\left(\begin{array}{ll} E & F \\ F & G \end{array}\right)$$

  Explain briefly the significance of the determinant $a d-b c$.

  comment

Groups, Rings and Modules

• 4.I.2C

  Groups, Rings and Modules | Part IB, 2005

  State Eisenstein's irreducibility criterion. Let $n$ be an integer $>1$. Prove that $1+x+\ldots+x^{n-1}$ is irreducible in $\mathbb{Z}[x]$ if and only if $n$ is a prime number.

  comment

• 4.II.11C

  Groups, Rings and Modules | Part IB, 2005

  Let $R$ be the ring of Gaussian integers $\mathbb{Z}[i]$, where $i^{2}=-1$, which you may assume to be a unique factorization domain. Prove that every prime element of $R$ divides precisely one positive prime number in $\mathbb{Z}$. List, without proof, the prime elements of $R$, up to associates.

  Let $p$ be a prime number in $\mathbb{Z}$. Prove that $R / p R$ has cardinality $p^{2}$. Prove that $R / 2 R$ is not a field. If $p \equiv 3 \bmod 4$, show that $R / p R$ is a field. If $p \equiv 1 \bmod 4$, decide whether $R / p R$ is a field or not, justifying your answer.

  comment

Linear Algebra

• 4.I.1B

  Linear Algebra | Part IB, 2005

  Define what it means for an $n \times n$ complex matrix to be unitary or Hermitian. Show that every eigenvalue of a Hermitian matrix is real. Show that every eigenvalue of a unitary matrix has absolute value 1 .

  Show that two eigenvectors of a Hermitian matrix that correspond to different eigenvalues are orthogonal, using the standard inner product on $\mathbf{C}^{n}$.

  comment

• 4.II.10B

  Linear Algebra | Part IB, 2005

  (i) Let $V$ be a finite-dimensional real vector space with an inner product. Let $e_{1}, \ldots, e_{n}$ be a basis for $V$. Prove by an explicit construction that there is an orthonormal basis $f_{1}, \ldots, f_{n}$ for $V$ such that the span of $e_{1}, \ldots, e_{i}$ is equal to the span of $f_{1}, \ldots, f_{i}$ for every $1 \leqslant i \leqslant n$.

  (ii) For any real number $a$, consider the quadratic form

  $$q_{a}(x, y, z)=x y+y z+z x+a x^{2}$$

  on $\mathbf{R}^{3}$. For which values of $a$ is $q_{a}$ nondegenerate? When $q_{a}$ is nondegenerate, compute its signature in terms of $a$.

  comment

Markov Chains

• 4.I.9D

  Markov Chains | Part IB, 2005

  Prove that the simple symmetric random walk in three dimensions is transient.

  [You may wish to recall Stirling's formula: $n ! \sim(2 \pi)^{\frac{1}{2}} n^{n+\frac{1}{2}} e^{-n} .$ ]

  comment

Methods

• 4.I.5H

  Methods | Part IB, 2005

  Show how the general solution of the wave equation for $y(x, t)$,

  $$\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} y(x, t)-\frac{\partial^{2}}{\partial x^{2}} y(x, t)=0$$

  can be expressed as

  $$y(x, t)=f(c t-x)+g(c t+x) .$$

  Show that the boundary conditions $y(0, t)=y(L, t)=0$ relate the functions $f$ and $g$ and require them to be periodic with period $2 L$.

  Show that, with these boundary conditions,

  $$\frac{1}{2} \int_{0}^{L}\left(\frac{1}{c^{2}}\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right) \mathrm{d} x=\int_{-L}^{L} g^{\prime}(c t+x)^{2} \mathrm{~d} x$$

  and that this is a constant independent of $t$.

  comment

• 4.II.16H

  Methods | Part IB, 2005

  Define an isotropic tensor and show that $\delta_{i j}, \epsilon_{i j k}$ are isotropic tensors.

  For $\hat{\mathbf{x}}$ a unit vector and $\mathrm{d} S(\hat{\mathbf{x}})$ the area element on the unit sphere show that

  $$\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i_{1}} \ldots \hat{x}_{i_{n}}$$

  is an isotropic tensor for any $n$. Hence show that

  $$\begin{aligned} &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j}=a \delta_{i j}, \quad \int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k}=0 \\ &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k} \hat{x}_{l}=b\left(\delta_{i j} \delta_{k l}+\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) \end{aligned}$$

  for some $a, b$ which should be determined.

  Explain why

  $$\int_{V} \mathrm{~d}^{3} x\left(x_{1}+\sqrt{-1} x_{2}\right)^{n} f(|\mathbf{x}|)=0, \quad n=2,3,4$$

  where $V$ is the region inside the unit sphere.

  [The general isotropic tensor of rank 4 has the form $a \delta_{i j} \delta_{k l}+b \delta_{i k} \delta_{j l}+c \delta_{i l} \delta_{j k} .$ ]

  comment

Metric and Topological Spaces

• 4.II.14A

  Metric and Topological Spaces | Part IB, 2005

  Let $(M, d)$ be a metric space, and $F$ a non-empty closed subset of $M$. For $x \in M$, set

  $$d(x, F)=\inf _{z \in F} d(x, z)$$

  Prove that $d(x, F)$ is a continuous function of $x$, and that it is strictly positive for $x \notin F$.

  A topological space is called normal if for any pair of disjoint closed subsets $F_{1}, F_{2}$, there exist disjoint open subsets $U_{1} \supset F_{1}, U_{2} \supset F_{2}$. By considering the function

  $$d\left(x, F_{1}\right)-d\left(x, F_{2}\right)$$

  or otherwise, deduce that any metric space is normal.

  Suppose now that $X$ is a normal topological space, and that $F_{1}, F_{2}$ are disjoint closed subsets in $X$. Prove that there exist open subsets $W_{1} \supset F_{1}, W_{2} \supset F_{2}$, whose closures are disjoint. In the case when $X=\mathbf{R}^{2}$ with the standard metric topology, $F_{1}=\{(x,-1 / x): x<0\}$ and $F_{2}=\{(x, 1 / x): x>0\}$, find explicit open subsets $W_{1}, W_{2}$ with the above property.

  comment

Numerical Analysis

• 4.I.8F

  Numerical Analysis | Part IB, 2005

  Define Gaussian quadrature.

  Evaluate the coefficients of the Gaussian quadrature of the integral

  $$\int_{-1}^{1}\left(1-x^{2}\right) f(x) d x$$

  which uses two function evaluations.

  comment

Optimization

• 4.II.20D

  Optimization | Part IB, 2005

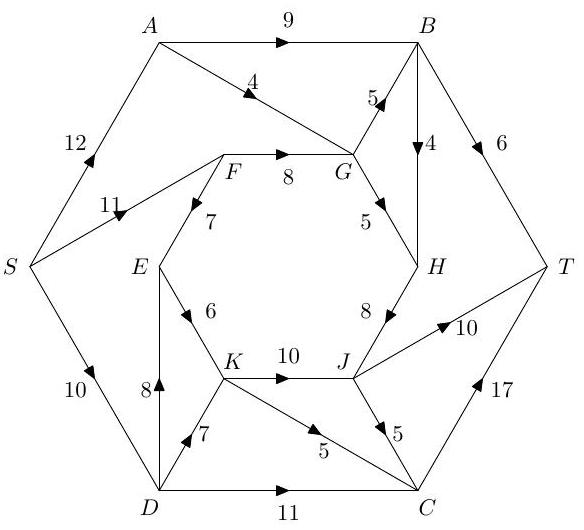
  Describe the Ford-Fulkerson algorithm for finding a maximal flow from a source to a sink in a directed network with capacity constraints on the arcs. Explain why the algorithm terminates at an optimal flow when the initial flow and the capacity constraints are rational.

  Illustrate the algorithm by applying it to the problem of finding a maximal flow from $S$ to $T$ in the network below.

  

  comment

Quantum Mechanics

• 4.I.6G

  Quantum Mechanics | Part IB, 2005

  Define the commutator $[A, B]$ of two operators, $A$ and $B$. In three dimensions angular momentum is defined by a vector operator $\mathbf{L}$ with components

  $$L_{x}=y p_{z}-z p_{y} \quad L_{y}=z p_{x}-x p_{z} \quad L_{z}=x p_{y}-y p_{x}$$

  Show that $\left[L_{x}, L_{y}\right]=i \hbar L_{z}$ and use this, together with permutations, to show that $\left[\mathbf{L}^{2}, L_{w}\right]=0$, where $w$ denotes any of the directions $x, y, z$.

  At a given time the wave function of a particle is given by

  $$\psi=(x+y+z) \exp \left(-\sqrt{x^{2}+y^{2}+z^{2}}\right)$$

  Show that this is an eigenstate of $\mathbf{L}^{2}$ with eigenvalue equal to $2 \hbar^{2}$.

  comment

Special Relativity

• 4.II.17G

  Special Relativity | Part IB, 2005

  Obtain the Lorentz transformations that relate the coordinates of an event measured in one inertial frame $(t, x, y, z)$ to those in another inertial frame moving with velocity $v$ along the $x$ axis. Take care to state the assumptions that lead to your result.

  A star is at rest in a three-dimensional coordinate frame $\mathcal{S}^{\prime}$ that is moving at constant velocity $v$ along the $x$ axis of a second coordinate frame $\mathcal{S}$. The star emits light of frequency $\nu^{\prime}$, which may considered to be a beam of photons. A light ray from the star to the origin in $\mathcal{S}^{\prime}$ is a straight line that makes an angle $\theta^{\prime}$ with the $x^{\prime}$ axis. Write down the components of the four-momentum of a photon in this light ray.

  The star is seen by an observer at rest at the origin of $\mathcal{S}$ at time $t=t^{\prime}=0$, when the origins of the coordinate frames $\mathcal{S}$ and $\mathcal{S}^{\prime}$ coincide. The light that reaches the observer moves along a line through the origin that makes an angle $\theta$ to the $x$ axis and has frequency $\nu$. Make use of the Lorentz transformations between the four-momenta of a photon in these two frames to determine the relation

  $$\lambda=\lambda^{\prime}\left(1-\frac{v^{2}}{c^{2}}\right)^{-1 / 2}\left(1+\frac{v}{c} \cos \theta\right)$$

  where $\lambda$ is the observed wavelength of the photon and $\lambda^{\prime}$ is the wavelength in the star's rest frame.

  Comment on the form of this result in the special cases with $\cos \theta=1, \cos \theta=-1$ and $\cos \theta=0$.

  [You may assume that the energy of a photon of frequency $\nu \mathrm{~ i s ~ h}$ momentum is a three-vector of magnitude $h \nu / c .]$

  comment

Statistics

• 4.II.19D

  Statistics | Part IB, 2005

  Let $Y_{1}, \ldots, Y_{n}$ be observations satisfying

  $$Y_{i}=\beta x_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent random variables each with the $N\left(0, \sigma^{2}\right)$ distribution. Here $x_{1}, \ldots, x_{n}$ are known but $\beta$ and $\sigma^{2}$ are unknown.

  (i) Determine the maximum-likelihood estimates $\left(\widehat{\beta}, \widehat{\sigma}^{2}\right)$ of $\left(\beta, \sigma^{2}\right)$.

  (ii) Find the distribution of $\widehat{\beta}$.

  (iii) By showing that $Y_{i}-\widehat{\beta} x_{i}$ and $\widehat{\beta}$ are independent, or otherwise, determine the joint distribution of $\widehat{\beta}$ and $\widehat{\sigma}^{2}$.

  (iv) Explain carefully how you would test the hypothesis $H_{0}: \beta=\beta_{0}$ against $H_{1}: \beta \neq \beta_{0}$.

  comment