Part IA, 2020, Paper 2

Dynamics and Relativity

• Paper 2, Section I, C

  Dynamics and Relativity | Part IA, 2020

  A particle $P$ with unit mass moves in a central potential $\Phi(r)=-k / r$ where $k>0$. Initially $P$ is a distance $R$ away from the origin moving with speed $u$ on a trajectory which, in the absence of any force, would be a straight line whose shortest distance from the origin is $b$. The shortest distance between $P$ 's actual trajectory and the origin is $p$, with $0<p<b$, at which point it is moving with speed $w$.

  (i) Assuming $u^{2} \gg 2 k / R$, find $w^{2} / k$ in terms of $b$ and $p$.

  (ii) Assuming $u^{2}<2 k / R$, find an expression for $P^{\prime}$ 's farthest distance from the origin $q$ in the form

  $$A q^{2}+B q+C=0$$

  where $A, B$, and $C$ depend only on $R, b, k$, and the angular momentum $L$.

  [You do not need to prove that energy and angular momentum are conserved.]

  comment

• Paper 2, Section II, C

  Dynamics and Relativity | Part IA, 2020

  (a) A moving particle with rest mass $M$ decays into two particles (photons) with zero rest mass. Derive an expression for $\sin \frac{\theta}{2}$, where $\theta$ is the angle between the spatial momenta of the final state particles, and show that it depends only on $M c^{2}$ and the energies of the massless particles. ( $c$ is the speed of light in vacuum.)

  (b) A particle $P$ with rest mass $M$ decays into two particles: a particle $R$ with rest mass $0<m<M$ and another particle with zero rest mass. Using dimensional analysis explain why the speed $v$ of $R$ in the rest frame of $P$ can be expressed as

  $$v=c f(r), \quad \text { with } \quad r=\frac{m}{M}$$

  and $f$ a dimensionless function of $r$. Determine the function $f(r)$.

  Choose coordinates in the rest frame of $P$ such that $R$ is emitted at $t=0$ from the origin in the $x$-direction. The particle $R$ decays after a time $\tau$, measured in its own rest frame. Determine the spacetime coordinates $(c t, x)$, in the rest frame of $P$, corresponding to this event.

  comment

• Paper 2, Section II, C

  Dynamics and Relativity | Part IA, 2020

  An axially symmetric pulley of mass $M$ rotates about a fixed, horizontal axis, say the $x$-axis. A string of fixed length and negligible mass connects two blocks with masses $m_{1}=M$ and $m_{2}=2 M$. The string is hung over the pulley, with one mass on each side. The tensions in the string due to masses $m_{1}$ and $m_{2}$ can respectively be labelled $T_{1}$ and $T_{2}$. The moment of inertia of the pulley is $I=q M a^{2}$, where $q$ is a number and $a$ is the radius of the

  

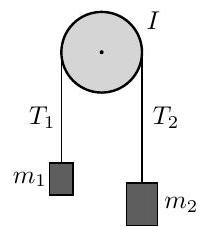
  The motion of the pulley is opposed by a frictional torque of magnitude $\lambda M \omega$, where $\omega$ is the angular velocity of the pulley and $\lambda$ is a real positive constant. Obtain a first-order differential equation for $\omega$ and, from it, find $\omega(t)$ given that the system is released from rest.

  The surface of the pulley is defined by revolving the function $b(x)$ about the $x$-axis, with

  $$b(x)= \begin{cases}a(1+|x|) & -1 \leqslant x \leqslant 1 \\ 0 & \text { otherwise. }\end{cases}$$

  Find a value for the constant $q$ given that the pulley has uniform mass density $\rho$.

  comment

Groups

• Paper 2, Section I, E

  Groups | Part IA, 2020

  What does it mean for an element of the symmetric group $S_{n}$ to be a transposition or a cycle?

  Let $n \geqslant 4$. How many permutations $\sigma$ of $\{1,2, \ldots, n\}$ are there such that

  (i) $\sigma(1)=2 ?$

  (ii) $\sigma(k)$ is even for each even number $k$ ?

  (iii) $\sigma$ is a 4-cycle?

  (iv) $\sigma$ can be written as the product of two transpositions?

  You should indicate in each case how you have derived your formula.

  comment

• Paper 2, Section II, E

  Groups | Part IA, 2020

  (a) Let $G$ be a finite group acting on a finite set $X$. For any subset $T$ of $G$, we define the fixed point set as $X^{T}=\{x \in X: \forall g \in T, g \cdot x=x\}$. Write $X^{g}$ for $X^{\{g\}}(g \in G)$. Let $G \backslash X$ be the set of $G$-orbits in $X$. In what follows you may assume the orbit-stabiliser theorem.

  Prove that

  $$|X|=\left|X^{G}\right|+\sum_{x}|G| /\left|G_{x}\right|$$

  where the sum is taken over a set of representatives for the orbits containing more than one element.

  By considering the set $Z=\{(g, x) \in G \times X: g \cdot x=x\}$, or otherwise, show also that

  $$|G \backslash X|=\frac{1}{|G|} \sum_{g \in G}\left|X^{g}\right|$$

  (b) Let $V$ be the set of vertices of a regular pentagon and let the dihedral group $D_{10}$ act on $V$. Consider the set $X_{n}$ of functions $F: V \rightarrow \mathbb{Z}_{n}$ (the integers mod $\left.n\right)$. Assume that $D_{10}$ and its rotation subgroup $C_{5}$ act on $X_{n}$ by the rule

  $$(g \cdot F)(v)=F\left(g^{-1} \cdot v\right),$$

  where $g \in D_{10}, F \in X_{n}$ and $v \in V$. It is given that $\left|X_{n}\right|=n^{5}$. We define a necklace to be a $C_{5}$-orbit in $X_{n}$ and a bracelet to be a $D_{10}$-orbit in $X_{n}$.

  Find the number of necklaces and bracelets for any $n$.

  comment

• Paper 2, Section II, E

  Groups | Part IA, 2020

  Suppose that $f$ is a Möbius transformation acting on the extended complex plane. Show that a Möbius transformation with at least three fixed points is the identity. Deduce that every Möbius transformation except the identity has one or two fixed points.

  Which of the following statements are true and which are false? Justify your answers, quoting standard facts if required.

  (i) If $f$ has exactly one fixed point then it is conjugate to $z \mapsto z+1$.

  (ii) Every Möbius transformation that fixes $\infty$ may be expressed as a composition of maps of the form $z \mapsto z+a$ and $z \mapsto \lambda z$ (where $a$ and $\lambda$ are complex numbers).

  (iii) Every Möbius transformation that fixes 0 may be expressed as a composition of maps of the form $z \mapsto \mu z$ and $z \mapsto 1 / z$ (where $\mu$ is a complex number).

  (iv) The operation of complex conjugation defined by $z \mapsto \bar{z}$ is a Möbius transformation.

  comment

Numbers and Sets

• Paper 2, Section I, $2 \mathrm{D}$

  Numbers and Sets | Part IA, 2020

  Define an equivalence relation. Which of the following is an equivalence relation on the set of non-zero complex numbers? Justify your answers. (i) $x \sim y$ if $|x-y|^{2}<|x|^{2}+|y|^{2}$. (ii) $x \sim y$ if $|x+y|=|x|+|y|$. (iii) $x \sim y$ if $\left|\frac{x}{y^{n}}\right|$ is rational for some integer $n \geqslant 1$. (iv) $x \sim y$ if $\left|x^{3}-x\right|=\left|y^{3}-y\right|$.

  comment

• Paper 2, Section II, D

  Numbers and Sets | Part IA, 2020

  (a) Define what it means for a set to be countable. Prove that $\mathbb{N} \times \mathbb{Z}$ is countable, and that the power set of $\mathbb{N}$ is uncountable.

  (b) Let $\sigma: X \rightarrow Y$ be a bijection. Show that if $f: X \rightarrow X$ and $g: Y \rightarrow Y$ are related by $g=\sigma f \sigma^{-1}$ then they have the same number of fixed points.

  [A fixed point of $f$ is an element $x \in X$ such that $f(x)=x$.]

  (c) Let $T$ be the set of bijections $f: \mathbb{N} \rightarrow \mathbb{N}$ with the property that no iterate of $f$ has a fixed point.

  [The $k^{\text {th }}$iterate of $f$ is the map obtained by $k$ successive applications of $f$.]

  (i) Write down an explicit element of $T$.

  (ii) Determine whether $T$ is countable or uncountable.

  comment

• Paper 2, Section II, D

  Numbers and Sets | Part IA, 2020

  (a) Define the Euler function $\phi(n)$. State the Chinese remainder theorem, and use it to derive a formula for $\phi(n)$ when $n=p_{1} p_{2} \ldots p_{r}$ is a product of distinct primes. Show that there are at least ten odd numbers $n$ with $\phi(n)$ a power of 2 .

  (b) State and prove the Fermat-Euler theorem.

  (c) In the RSA cryptosystem a message $m \in\{1,2, \ldots, N-1\}$ is encrypted as $c=m^{e}$ $(\bmod N)$. Explain how $N$ and $e$ should be chosen, and how (given a factorisation of $N$ ) to compute the decryption exponent $d$. Prove that your choice of $d$ works, subject to reasonable assumptions on $m$. If $N=187$ and $e=13$ then what is $d$ ?

  comment

Vector Calculus

• Paper 2, Section I, B

  Vector Calculus | Part IA, 2020

  (a) Evaluate the line integral

  $$\int_{(0,1)}^{(1,2)}\left(x^{2}-y\right) d x+\left(y^{2}+x\right) d y$$

  along

  (i) a straight line from $(0,1)$ to $(1,2)$,

  (ii) the parabola $x=t, y=1+t^{2}$.

  (b) State Green's theorem. The curve $C_{1}$ is the circle of radius $a$ centred on the origin and traversed anticlockwise and $C_{2}$ is another circle of radius $b<a$ traversed clockwise and completely contained within $C_{1}$ but may or may not be centred on the origin. Find

  $$\int_{C_{1} \cup C_{2}} y(x y-\lambda) d x+x^{2} y d y$$

  as a function of $\lambda$.

  comment

• Paper 2, Section II, B

  Vector Calculus | Part IA, 2020

  (a) State the value of $\partial x_{i} / \partial x_{j}$ and find $\partial r / \partial x_{j}$ where $r=|\boldsymbol{x}|$.

  (b) A vector field $\boldsymbol{u}$ is given by

  $$\boldsymbol{u}=\frac{\boldsymbol{a}}{r}+\frac{(\boldsymbol{a} \cdot \boldsymbol{x}) \boldsymbol{x}}{r^{3}}$$

  where $\boldsymbol{a}$ is a constant vector. Calculate the second-rank tensor $d_{i j}=\partial u_{i} / \partial x_{j}$ using suffix notation and show how $d_{i j}$ splits naturally into symmetric and antisymmetric parts. Show that

  $$\nabla \cdot \boldsymbol{u}=0$$

  and

  $$\nabla \times u=\frac{2 a \times x}{r^{3}}$$

  (c) Consider the equation

  $$\nabla^{2} u=f$$

  on a bounded domain $V \subset \mathbb{R}^{3}$ subject to the mixed boundary condition

  $$(1-\lambda) u+\lambda \frac{d u}{d n}=0$$

  on the smooth boundary $S=\partial V$, where $\lambda \in[0,1)$ is a constant. Show that if a solution exists, it will be unique.

  Find the spherically symmetric solution $u(r)$ for the choice $f=6$ in the region $r=|\boldsymbol{x}| \leqslant b$ for $b>0$, as a function of the constant $\lambda \in[0,1)$. Explain why a solution does not exist for $\lambda=1$

  comment

• Paper 2, Section II, B

  Vector Calculus | Part IA, 2020

  Write down Stokes' theorem for a vector field $\mathbf{A}(\mathbf{x})$ on $\mathbb{R}^{3}$.

  Let the surface $S$ be the part of the inverted paraboloid

  $$z=5-x^{2}-y^{2}, \quad 1<z<4$$

  and the vector field $\mathbf{A}(\mathbf{x})=\left(3 y,-x z, y z^{2}\right)$.

  (a) Sketch the surface $S$ and directly calculate $I=\int_{S}(\nabla \times \mathbf{A}) \cdot d \mathbf{S}$.

  (b) Now calculate $I$ a different way by using Stokes' theorem.

  comment