Part IA, 2020

Analysis I

• Paper 1, Section I, E

  Analysis I | Part IA, 2020

  (a) Let $f$ be continuous in $[a, b]$, and let $g$ be strictly monotonic in $[\alpha, \beta]$, with a continuous derivative there, and suppose that $a=g(\alpha)$ and $b=g(\beta)$. Prove that

  $$\int_{a}^{b} f(x) d x=\int_{\alpha}^{\beta} f(g(u)) g^{\prime}(u) d u$$

  [Any version of the fundamental theorem of calculus may be used providing it is quoted correctly.]

  (b) Justifying carefully the steps in your argument, show that the improper Riemann integral

  $$\int_{0}^{e^{-1}} \frac{d x}{x\left(\log \frac{1}{x}\right)^{\theta}}$$

  converges for $\theta>1$, and evaluate it.

  comment

• Paper 1, Section II, D

  Analysis I | Part IA, 2020

  (a) State Rolle's theorem. Show that if $f: \mathbb{R} \rightarrow \mathbb{R}$ is $N+1$ times differentiable and $x \in \mathbb{R}$ then

  $$f(x)=f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\ldots+\frac{f^{(N)}(0)}{N !} x^{N}+\frac{f^{(N+1)}(\theta x)}{(N+1) !} x^{N+1}$$

  for some $0<\theta<1$. Hence, or otherwise, show that if $f^{\prime}(x)=0$ for all $x \in \mathbb{R}$ then $f$ is constant.

  (b) Let $s: \mathbb{R} \rightarrow \mathbb{R}$ and $c: \mathbb{R} \rightarrow \mathbb{R}$ be differentiable functions such that

  $$s^{\prime}(x)=c(x), \quad c^{\prime}(x)=-s(x), \quad s(0)=0 \quad \text { and } \quad c(0)=1$$

  Prove that (i) $s(x) c(a-x)+c(x) s(a-x)$ is independent of $x$, (ii) $s(x+y)=s(x) c(y)+c(x) s(y)$, (iii) $s(x)^{2}+c(x)^{2}=1$.

  Show that $c(1)>0$ and $c(2)<0$. Deduce there exists $1<k<2$ such that $s(2 k)=c(k)=0$ and $s(x+4 k)=s(x)$.

  comment

• Paper 1, Section II, F

  Analysis I | Part IA, 2020

  (a) Let $\left(x_{n}\right)$ be a bounded sequence of real numbers. Show that $\left(x_{n}\right)$ has a convergent subsequence.

  (b) Let $\left(z_{n}\right)$ be a bounded sequence of complex numbers. For each $n \geqslant 1$, write $z_{n}=x_{n}+i y_{n}$. Show that $\left(z_{n}\right)$ has a subsequence $\left(z_{n_{j}}\right)$ such that $\left(x_{n_{j}}\right)$ converges. Hence, or otherwise, show that $\left(z_{n}\right)$ has a convergent subsequence.

  (c) Write $\mathbb{N}=\{1,2,3, \ldots\}$ for the set of positive integers. Let $M$ be a positive real number, and for each $i \in \mathbb{N}$, let $X^{(i)}=\left(x_{1}^{(i)}, x_{2}^{(i)}, x_{3}^{(i)}, \ldots\right)$ be a sequence of real numbers with $\left|x_{j}^{(i)}\right| \leqslant M$ for all $i, j \in \mathbb{N}$. By induction on $i$ or otherwise, show that there exist sequences $N^{(i)}=\left(n_{1}^{(i)}, n_{2}^{(i)}, n_{3}^{(i)}, \ldots\right)$ of positive integers with the following properties:

  • for all $i \in \mathbb{N}$, the sequence $N^{(i)}$ is strictly increasing;

  • for all $i \in \mathbb{N}, N^{(i+1)}$ is a subsequence of $N^{(i)} ;$ and

  • for all $k \in \mathbb{N}$ and all $i \in \mathbb{N}$ with $1 \leqslant i \leqslant k$, the sequence

  $$\left(x_{n_{1}^{(k)}}^{(i)}, x_{n_{2}^{(k)}}^{(i)}, x_{n_{3}^{(k)}}^{(i)}, \ldots\right)$$

  converges.

  Hence, or otherwise, show that there exists a strictly increasing sequence $\left(m_{j}\right)$ of positive integers such that for all $i \in \mathbb{N}$ the sequence $\left(x_{m_{1}}^{(i)}, x_{m_{2}}^{(i)}, x_{m_{3}}^{(i)}, \ldots\right)$ converges.

  comment

Differential Equations

• Paper 1, Section I, A

  Differential Equations | Part IA, 2020

  Solve the differential equation

  $$\frac{d y}{d x}=\frac{1}{x+e^{2 y}}$$

  subject to the initial condition $y(1)=0$.

  comment

• Paper 1, Section II, A

  Differential Equations | Part IA, 2020

  Solve the system of differential equations for $x(t), y(t), z(t)$,

  $$\begin{aligned} &\dot{x}=3 z-x \\ &\dot{y}=3 x+2 y-3 z+\cos t-2 \sin t \\ &\dot{z}=3 x-z \end{aligned}$$

  subject to the initial conditions $x(0)=y(0)=0, z(0)=1$.

  comment

• Paper 1, Section II, A

  Differential Equations | Part IA, 2020

  Show that for each $t>0$ and $x \in \mathbb{R}$ the function

  $$K(x, t)=\frac{1}{\sqrt{4 \pi t}} \exp \left(-\frac{x^{2}}{4 t}\right)$$

  satisfies the heat equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}$$

  For $t>0$ and $x \in \mathbb{R}$ define the function $u=u(x, t)$ by the integral

  $$u(x, t)=\int_{-\infty}^{\infty} K(x-y, t) f(y) d y$$

  Show that $u$ satisfies the heat equation and $\lim _{t \rightarrow 0^{+}} u(x, t)=f(x)$. [Hint: You may find it helpful to consider the substitution $Y=(x-y) / \sqrt{4 t}$.]

  Burgers' equation is

  $$\frac{\partial w}{\partial t}+w \frac{\partial w}{\partial x}=\frac{\partial^{2} w}{\partial x^{2}}$$

  By considering the transformation

  $$w(x, t)=-2 \frac{1}{u} \frac{\partial u}{\partial x}$$

  solve Burgers' equation with the initial condition $\lim _{t \rightarrow 0^{+}} w(x, t)=g(x)$.

  comment

Dynamics and Relativity

• Paper 2, Section I, C

  Dynamics and Relativity | Part IA, 2020

  A particle $P$ with unit mass moves in a central potential $\Phi(r)=-k / r$ where $k>0$. Initially $P$ is a distance $R$ away from the origin moving with speed $u$ on a trajectory which, in the absence of any force, would be a straight line whose shortest distance from the origin is $b$. The shortest distance between $P$ 's actual trajectory and the origin is $p$, with $0<p<b$, at which point it is moving with speed $w$.

  (i) Assuming $u^{2} \gg 2 k / R$, find $w^{2} / k$ in terms of $b$ and $p$.

  (ii) Assuming $u^{2}<2 k / R$, find an expression for $P^{\prime}$ 's farthest distance from the origin $q$ in the form

  $$A q^{2}+B q+C=0$$

  where $A, B$, and $C$ depend only on $R, b, k$, and the angular momentum $L$.

  [You do not need to prove that energy and angular momentum are conserved.]

  comment

• Paper 2, Section II, C

  Dynamics and Relativity | Part IA, 2020

  (a) A moving particle with rest mass $M$ decays into two particles (photons) with zero rest mass. Derive an expression for $\sin \frac{\theta}{2}$, where $\theta$ is the angle between the spatial momenta of the final state particles, and show that it depends only on $M c^{2}$ and the energies of the massless particles. ( $c$ is the speed of light in vacuum.)

  (b) A particle $P$ with rest mass $M$ decays into two particles: a particle $R$ with rest mass $0<m<M$ and another particle with zero rest mass. Using dimensional analysis explain why the speed $v$ of $R$ in the rest frame of $P$ can be expressed as

  $$v=c f(r), \quad \text { with } \quad r=\frac{m}{M}$$

  and $f$ a dimensionless function of $r$. Determine the function $f(r)$.

  Choose coordinates in the rest frame of $P$ such that $R$ is emitted at $t=0$ from the origin in the $x$-direction. The particle $R$ decays after a time $\tau$, measured in its own rest frame. Determine the spacetime coordinates $(c t, x)$, in the rest frame of $P$, corresponding to this event.

  comment

• Paper 2, Section II, C

  Dynamics and Relativity | Part IA, 2020

  An axially symmetric pulley of mass $M$ rotates about a fixed, horizontal axis, say the $x$-axis. A string of fixed length and negligible mass connects two blocks with masses $m_{1}=M$ and $m_{2}=2 M$. The string is hung over the pulley, with one mass on each side. The tensions in the string due to masses $m_{1}$ and $m_{2}$ can respectively be labelled $T_{1}$ and $T_{2}$. The moment of inertia of the pulley is $I=q M a^{2}$, where $q$ is a number and $a$ is the radius of the

  

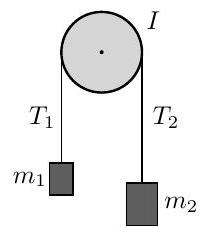
  The motion of the pulley is opposed by a frictional torque of magnitude $\lambda M \omega$, where $\omega$ is the angular velocity of the pulley and $\lambda$ is a real positive constant. Obtain a first-order differential equation for $\omega$ and, from it, find $\omega(t)$ given that the system is released from rest.

  The surface of the pulley is defined by revolving the function $b(x)$ about the $x$-axis, with

  $$b(x)= \begin{cases}a(1+|x|) & -1 \leqslant x \leqslant 1 \\ 0 & \text { otherwise. }\end{cases}$$

  Find a value for the constant $q$ given that the pulley has uniform mass density $\rho$.

  comment

Groups

• Paper 2, Section I, E

  Groups | Part IA, 2020

  What does it mean for an element of the symmetric group $S_{n}$ to be a transposition or a cycle?

  Let $n \geqslant 4$. How many permutations $\sigma$ of $\{1,2, \ldots, n\}$ are there such that

  (i) $\sigma(1)=2 ?$

  (ii) $\sigma(k)$ is even for each even number $k$ ?

  (iii) $\sigma$ is a 4-cycle?

  (iv) $\sigma$ can be written as the product of two transpositions?

  You should indicate in each case how you have derived your formula.

  comment

• Paper 2, Section II, E

  Groups | Part IA, 2020

  (a) Let $G$ be a finite group acting on a finite set $X$. For any subset $T$ of $G$, we define the fixed point set as $X^{T}=\{x \in X: \forall g \in T, g \cdot x=x\}$. Write $X^{g}$ for $X^{\{g\}}(g \in G)$. Let $G \backslash X$ be the set of $G$-orbits in $X$. In what follows you may assume the orbit-stabiliser theorem.

  Prove that

  $$|X|=\left|X^{G}\right|+\sum_{x}|G| /\left|G_{x}\right|$$

  where the sum is taken over a set of representatives for the orbits containing more than one element.

  By considering the set $Z=\{(g, x) \in G \times X: g \cdot x=x\}$, or otherwise, show also that

  $$|G \backslash X|=\frac{1}{|G|} \sum_{g \in G}\left|X^{g}\right|$$

  (b) Let $V$ be the set of vertices of a regular pentagon and let the dihedral group $D_{10}$ act on $V$. Consider the set $X_{n}$ of functions $F: V \rightarrow \mathbb{Z}_{n}$ (the integers mod $\left.n\right)$. Assume that $D_{10}$ and its rotation subgroup $C_{5}$ act on $X_{n}$ by the rule

  $$(g \cdot F)(v)=F\left(g^{-1} \cdot v\right),$$

  where $g \in D_{10}, F \in X_{n}$ and $v \in V$. It is given that $\left|X_{n}\right|=n^{5}$. We define a necklace to be a $C_{5}$-orbit in $X_{n}$ and a bracelet to be a $D_{10}$-orbit in $X_{n}$.

  Find the number of necklaces and bracelets for any $n$.

  comment

• Paper 2, Section II, E

  Groups | Part IA, 2020

  Suppose that $f$ is a Möbius transformation acting on the extended complex plane. Show that a Möbius transformation with at least three fixed points is the identity. Deduce that every Möbius transformation except the identity has one or two fixed points.

  Which of the following statements are true and which are false? Justify your answers, quoting standard facts if required.

  (i) If $f$ has exactly one fixed point then it is conjugate to $z \mapsto z+1$.

  (ii) Every Möbius transformation that fixes $\infty$ may be expressed as a composition of maps of the form $z \mapsto z+a$ and $z \mapsto \lambda z$ (where $a$ and $\lambda$ are complex numbers).

  (iii) Every Möbius transformation that fixes 0 may be expressed as a composition of maps of the form $z \mapsto \mu z$ and $z \mapsto 1 / z$ (where $\mu$ is a complex number).

  (iv) The operation of complex conjugation defined by $z \mapsto \bar{z}$ is a Möbius transformation.

  comment

Numbers and Sets

• Paper 2, Section I, $2 \mathrm{D}$

  Numbers and Sets | Part IA, 2020

  Define an equivalence relation. Which of the following is an equivalence relation on the set of non-zero complex numbers? Justify your answers. (i) $x \sim y$ if $|x-y|^{2}<|x|^{2}+|y|^{2}$. (ii) $x \sim y$ if $|x+y|=|x|+|y|$. (iii) $x \sim y$ if $\left|\frac{x}{y^{n}}\right|$ is rational for some integer $n \geqslant 1$. (iv) $x \sim y$ if $\left|x^{3}-x\right|=\left|y^{3}-y\right|$.

  comment

• Paper 2, Section II, D

  Numbers and Sets | Part IA, 2020

  (a) Define what it means for a set to be countable. Prove that $\mathbb{N} \times \mathbb{Z}$ is countable, and that the power set of $\mathbb{N}$ is uncountable.

  (b) Let $\sigma: X \rightarrow Y$ be a bijection. Show that if $f: X \rightarrow X$ and $g: Y \rightarrow Y$ are related by $g=\sigma f \sigma^{-1}$ then they have the same number of fixed points.

  [A fixed point of $f$ is an element $x \in X$ such that $f(x)=x$.]

  (c) Let $T$ be the set of bijections $f: \mathbb{N} \rightarrow \mathbb{N}$ with the property that no iterate of $f$ has a fixed point.

  [The $k^{\text {th }}$iterate of $f$ is the map obtained by $k$ successive applications of $f$.]

  (i) Write down an explicit element of $T$.

  (ii) Determine whether $T$ is countable or uncountable.

  comment

• Paper 2, Section II, D

  Numbers and Sets | Part IA, 2020

  (a) Define the Euler function $\phi(n)$. State the Chinese remainder theorem, and use it to derive a formula for $\phi(n)$ when $n=p_{1} p_{2} \ldots p_{r}$ is a product of distinct primes. Show that there are at least ten odd numbers $n$ with $\phi(n)$ a power of 2 .

  (b) State and prove the Fermat-Euler theorem.

  (c) In the RSA cryptosystem a message $m \in\{1,2, \ldots, N-1\}$ is encrypted as $c=m^{e}$ $(\bmod N)$. Explain how $N$ and $e$ should be chosen, and how (given a factorisation of $N$ ) to compute the decryption exponent $d$. Prove that your choice of $d$ works, subject to reasonable assumptions on $m$. If $N=187$ and $e=13$ then what is $d$ ?

  comment

Probability

• Paper 1, Section I, F

  Probability | Part IA, 2020

  A robot factory begins with a single generation-0 robot. Each generation- $n$ robot independently builds some number of generation- $(n+1)$ robots before breaking down. The number of generation- $(n+1)$ robots built by a generation- $n$ robot is $0,1,2$ or 3 with probabilities $\frac{1}{12}, \frac{1}{2}, \frac{1}{3}$ and $\frac{1}{12}$ respectively. Find the expectation of the total number of generation- $n$ robots produced by the factory. What is the probability that the factory continues producing robots forever?

  [Standard results about branching processes may be used without proof as long as they are carefully stated.]

  comment

• Paper 1, Section II, F

  Probability | Part IA, 2020

  (a) Let $Z$ be a $N(0,1)$ random variable. Write down the probability density function (pdf) of $Z$, and verify that it is indeed a pdf. Find the moment generating function (mgf) $m_{Z}(\theta)=\mathbb{E}\left(e^{\theta Z}\right)$ of $Z$ and hence, or otherwise, verify that $Z$ has mean 0 and variance 1 .

  (b) Let $\left(X_{n}\right)_{n \geqslant 1}$ be a sequence of IID $N(0,1)$ random variables. Let $S_{n}=\sum_{i=1}^{n} X_{i}$ and let $U_{n}=S_{n} / \sqrt{n}$. Find the distribution of $U_{n}$.

  (c) Let $Y_{n}=X_{n}^{2}$. Find the mean $\mu$ and variance $\sigma^{2}$ of $Y_{1}$. Let $T_{n}=\sum_{i=1}^{n} Y_{i}$ and let $V_{n}=\left(T_{n}-n \mu\right) / \sigma \sqrt{n}$.

  If $\left(W_{n}\right)_{n \geqslant 1}$ is a sequence of random variables and $W$ is a random variable, what does it mean to say that $W_{n} \rightarrow W$ in distribution? State carefully the continuity theorem and use it to show that $V_{n} \rightarrow Z$ in distribution.

  [You may not assume the central limit theorem.]

  comment

• Paper 1, Section II, F

  Probability | Part IA, 2020

  Let $A_{1}, A_{2}, \ldots, A_{n}$ be events in some probability space. State and prove the inclusion-exclusion formula for the probability $\mathbb{P}\left(\bigcup_{i=1}^{n} A_{i}\right)$. Show also that

  $$\mathbb{P}\left(\bigcup_{i=1}^{n} A_{i}\right) \geqslant \sum_{i} \mathbb{P}\left(A_{i}\right)-\sum_{i<j} \mathbb{P}\left(A_{i} \cap A_{j}\right)$$

  Suppose now that $n \geqslant 2$ and that whenever $i \neq j$ we have $\mathbb{P}\left(A_{i} \cap A_{j}\right) \leqslant 1 / n$. Show that there is a constant $c$ independent of $n$ such that $\sum_{i=1}^{n} \mathbb{P}\left(A_{i}\right) \leqslant c \sqrt{n}$.

  comment

Vector Calculus

• Paper 2, Section I, B

  Vector Calculus | Part IA, 2020

  (a) Evaluate the line integral

  $$\int_{(0,1)}^{(1,2)}\left(x^{2}-y\right) d x+\left(y^{2}+x\right) d y$$

  along

  (i) a straight line from $(0,1)$ to $(1,2)$,

  (ii) the parabola $x=t, y=1+t^{2}$.

  (b) State Green's theorem. The curve $C_{1}$ is the circle of radius $a$ centred on the origin and traversed anticlockwise and $C_{2}$ is another circle of radius $b<a$ traversed clockwise and completely contained within $C_{1}$ but may or may not be centred on the origin. Find

  $$\int_{C_{1} \cup C_{2}} y(x y-\lambda) d x+x^{2} y d y$$

  as a function of $\lambda$.

  comment

• Paper 2, Section II, B

  Vector Calculus | Part IA, 2020

  (a) State the value of $\partial x_{i} / \partial x_{j}$ and find $\partial r / \partial x_{j}$ where $r=|\boldsymbol{x}|$.

  (b) A vector field $\boldsymbol{u}$ is given by

  $$\boldsymbol{u}=\frac{\boldsymbol{a}}{r}+\frac{(\boldsymbol{a} \cdot \boldsymbol{x}) \boldsymbol{x}}{r^{3}}$$

  where $\boldsymbol{a}$ is a constant vector. Calculate the second-rank tensor $d_{i j}=\partial u_{i} / \partial x_{j}$ using suffix notation and show how $d_{i j}$ splits naturally into symmetric and antisymmetric parts. Show that

  $$\nabla \cdot \boldsymbol{u}=0$$

  and

  $$\nabla \times u=\frac{2 a \times x}{r^{3}}$$

  (c) Consider the equation

  $$\nabla^{2} u=f$$

  on a bounded domain $V \subset \mathbb{R}^{3}$ subject to the mixed boundary condition

  $$(1-\lambda) u+\lambda \frac{d u}{d n}=0$$

  on the smooth boundary $S=\partial V$, where $\lambda \in[0,1)$ is a constant. Show that if a solution exists, it will be unique.

  Find the spherically symmetric solution $u(r)$ for the choice $f=6$ in the region $r=|\boldsymbol{x}| \leqslant b$ for $b>0$, as a function of the constant $\lambda \in[0,1)$. Explain why a solution does not exist for $\lambda=1$

  comment

• Paper 2, Section II, B

  Vector Calculus | Part IA, 2020

  Write down Stokes' theorem for a vector field $\mathbf{A}(\mathbf{x})$ on $\mathbb{R}^{3}$.

  Let the surface $S$ be the part of the inverted paraboloid

  $$z=5-x^{2}-y^{2}, \quad 1<z<4$$

  and the vector field $\mathbf{A}(\mathbf{x})=\left(3 y,-x z, y z^{2}\right)$.

  (a) Sketch the surface $S$ and directly calculate $I=\int_{S}(\nabla \times \mathbf{A}) \cdot d \mathbf{S}$.

  (b) Now calculate $I$ a different way by using Stokes' theorem.

  comment

Vectors and Matrices

• Paper 1, Section I, C

  Vectors and Matrices | Part IA, 2020

  Given a non-zero complex number $z=x+i y$, where $x$ and $y$ are real, find expressions for the real and imaginary parts of the following functions of $z$ in terms of $x$ and $y$ :

  (i) $e^{z}$,

  (ii) $\sin z$

  (iii) $\frac{1}{z}-\frac{1}{\bar{z}}$,

  (iv) $z^{3}-z^{2} \bar{z}-z \bar{z}^{2}+\bar{z}^{3}$,

  where $\bar{z}$ is the complex conjugate of $z$.

  Now assume $x>0$ and find expressions for the real and imaginary parts of all solutions to

  (v) $w=\log z$.

  comment

• Paper 1, Section II, $\mathbf{6 A}$

  Vectors and Matrices | Part IA, 2020

  What does it mean to say an $n \times n$ matrix is Hermitian?

  What does it mean to say an $n \times n$ matrix is unitary?

  Show that the eigenvalues of a Hermitian matrix are real and that eigenvectors corresponding to distinct eigenvalues are orthogonal.

  Suppose that $A$ is an $n \times n$ Hermitian matrix with $n$ distinct eigenvalues $\lambda_{1}, \ldots, \lambda_{n}$ and corresponding normalised eigenvectors $\mathbf{u}_{1}, \ldots, \mathbf{u}_{n}$. Let $U$ denote the matrix whose columns are $\mathbf{u}_{1}, \ldots, \mathbf{u}_{n}$. Show directly that $U$ is unitary and $U D U^{\dagger}=A$, where $D$ is a diagonal matrix you should specify.

  If $U$ is unitary and $D$ diagonal, must it be the case that $U D U^{\dagger}$ is Hermitian? Give a proof or counterexample.

  Find a unitary matrix $U$ and a diagonal matrix $D$ such that

  $$U D U^{\dagger}=\left(\begin{array}{ccc} 2 & 0 & 3 i \\ 0 & 2 & 0 \\ -3 i & 0 & 2 \end{array}\right)$$

  comment

• Paper 1, Section II, C

  Vectors and Matrices | Part IA, 2020

  (a) Let $A, B$, and $C$ be three distinct points in the plane $\mathbb{R}^{2}$ which are not collinear, and let $\mathbf{a}, \mathbf{b}$, and $\mathbf{c}$ be their position vectors.

  Show that the set $L_{A B}$ of points in $\mathbb{R}^{2}$ equidistant from $A$ and $B$ is given by an equation of the form

  $$\mathbf{n}_{A B} \cdot \mathbf{x}=p_{A B},$$

  where $\mathbf{n}_{A B}$ is a unit vector and $p_{A B}$ is a scalar, to be determined. Show that $L_{A B}$ is perpendicular to $\overrightarrow{A B}$.

  Show that if $\mathbf{x}$ satisfies

  $$\mathbf{n}_{A B} \cdot \mathbf{x}=p_{A B} \quad \text { and } \quad \mathbf{n}_{B C} \cdot \mathbf{x}=p_{B C}$$

  then

  $$\mathbf{n}_{C A} \cdot \mathbf{x}=p_{C A} .$$

  How do you interpret this result geometrically?

  (b) Let $\mathbf{a}$ and $\mathbf{u}$ be constant vectors in $\mathbb{R}^{3}$. Explain why the vectors $\mathbf{x}$ satisfying

  $$\mathbf{x} \times \mathbf{u}=\mathbf{a} \times \mathbf{u}$$

  describe a line in $\mathbb{R}^{3}$. Find an expression for the shortest distance between two lines $\mathbf{x} \times \mathbf{u}_{k}=\mathbf{a}_{k} \times \mathbf{u}_{k}$, where $k=1,2$.

  comment