Part IA, 2008, Paper 4

Dynamics

• 4.I.3B

  Dynamics | Part IA, 2008

  Two particles of masses $m_{1}$ and $m_{2}$ have position vectors $\mathbf{r}_{1}(t)$ and $\mathbf{r}_{2}(t)$ at time $t$. The particle of mass $m_{1}$ experiences a force $\mathbf{f}$ and the particle of mass $m_{2}$ experiences a force $-\mathbf{f}$. Show that the centre of mass moves at a constant velocity, and derive an equation of motion for the relative separation $\mathbf{r}=\mathbf{r}_{1}-\mathbf{r}_{2}$.

  Now suppose that $\mathbf{f}=-k \mathbf{r}$, where $k$ is a positive constant. The particles are initially at rest a distance $d$ apart. Calculate how long it takes before they collide.

  comment

• 4.I.4B

  Dynamics | Part IA, 2008

  A damped pendulum is described by the equation

  $$\ddot{x}+2 k \dot{x}+\omega^{2} \sin x=0,$$

  where $k$ and $\omega$ are real positive constants. Determine the location of all the equilibrium points of the system. Classify the equilibrium points in the two cases $k>\omega$ and $k<\omega$.

  comment

• 4.II.10B

  Dynamics | Part IA, 2008

  A body of mass $m$ moves in the gravitational field of a much larger spherical object of mass $M$ located at the origin. Starting from the equations of motion

  $$\begin{aligned} \ddot{r}-r \dot{\theta}^{2} &=-\frac{G M}{r^{2}}, \\ r \ddot{\theta}+2 \dot{r} \dot{\theta} &=0, \end{aligned}$$

  show that:

  (i) the body moves in an orbit of the form

  $$\frac{h^{2} u}{G M}=1+e \cos \left(\theta-\theta_{0}\right)$$

  where $u=1 / r, h$ is the constant angular momentum per unit mass, and $e$ and $\theta_{0}$ are constants;

  (ii) the total energy of the body is

  $$E=\frac{m G^{2} M^{2}}{2 h^{2}}\left(e^{2}-1\right)$$

  A meteorite is moving very far from the Earth with speed $V$, and in the absence of the effect of the Earth's gravitational field would miss the Earth by a shortest distance $b$ (measured from the Earth's centre). Show that in the subsequent motion

  $$h=b V$$

  and

  $$e=\left[1+\frac{b^{2} V^{4}}{G^{2} M^{2}}\right]^{\frac{1}{2}}$$

  Use equation $(*)$ to find the distance of closest approach, and show that the meteorite will collide with the Earth if

  $$b<\left[R^{2}+\frac{2 G M R}{V^{2}}\right]^{\frac{1}{2}}$$

  where $R$ is the radius of the Earth.

  comment

• 4.II.11B

  Dynamics | Part IA, 2008

  An inertial reference frame $S$ and another reference frame $S^{\prime}$ have a common origin $O$, and $S^{\prime}$ rotates with angular velocity $\boldsymbol{\omega}(t)$ with respect to $S$. Show the following:

  (i) the rates of change of an arbitrary vector a $(t)$ in frames $S$ and $S^{\prime}$ are related by

  $$\left(\frac{d \mathbf{a}}{d t}\right)_{S}=\left(\frac{d \mathbf{a}}{d t}\right)_{S^{\prime}}+\boldsymbol{\omega} \times \mathbf{a}$$

  (ii) the accelerations in $S$ and $S^{\prime}$ are related by

  $$\left(\frac{d^{2} \mathbf{r}}{d t^{2}}\right)_{S}=\left(\frac{d^{2} \mathbf{r}}{d t^{2}}\right)_{S^{\prime}}+2 \boldsymbol{\omega} \times\left(\frac{d \mathbf{r}}{d t}\right)_{S^{\prime}}+\left(\frac{d \boldsymbol{\omega}}{d t}\right)_{S^{\prime}} \times \mathbf{r}+\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r})$$

  where $\mathbf{r}(t)$ is the position vector relative to $O$.

  A train of mass $m$ at latitude $\lambda$ in the Northern hemisphere travels North with constant speed $V$ along a track which runs North-South. Find the magnitude and direction of the sideways force exerted on the train by the track.

  comment

• 4.II.12B

  Dynamics | Part IA, 2008

  A uniform solid sphere has mass $m$ and radius $R_{0}$. Calculate the moment of inertia of the sphere about an axis through its centre.

  A long hollow circular cylinder of radius $R_{1}$ (where $R_{1}>2 R_{0}$ ) is held fixed with its axis horizontal. The sphere is held initially at rest in contact with the inner surface of the cylinder at $\theta=\alpha$, where $\alpha<\pi / 2$ and $\theta$ is the angle between the line joining the centre of the sphere to the cylinder axis and the downward vertical, as shown in the figure.

  

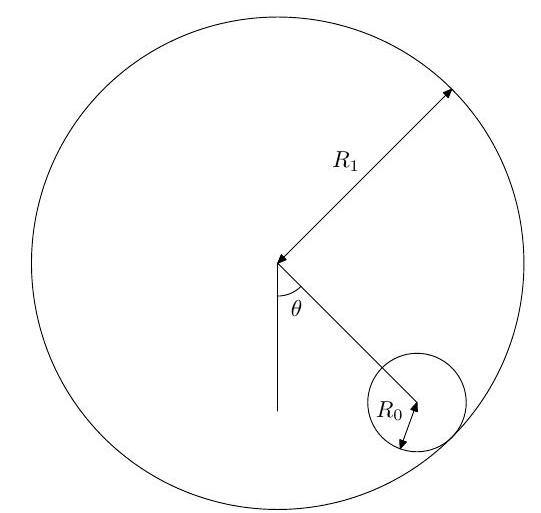
  The sphere is then released, and rolls without slipping. Show that the angular velocity of the sphere is

  $$\left(\frac{R_{1}-R_{0}}{R_{0}}\right) \dot{\theta} .$$

  Show further that the time, $T_{R}$, it takes the sphere to reach $\theta=0$ is

  $$T_{R}=\sqrt{\frac{7\left(R_{1}-R_{0}\right)}{10 g}} \quad \int_{0}^{\alpha} \frac{d \theta}{(\cos \theta-\cos \alpha)^{\frac{1}{2}}}$$

  If, instead, the cylinder and sphere surfaces are highly polished, so that the sphere now slides without rolling, find the time, $T_{S}$, it takes to reach $\theta=0$.

  Without further calculation, explain qualitatively how your answers for $T_{R}$ and $T_{S}$ would be affected if the solid sphere were replaced by a hollow spherical shell of the same radius and mass.

  comment

• 4.II.9B

  Dynamics | Part IA, 2008

  An octopus of mass $m_{o}$ swims horizontally in a straight line by jet propulsion. At time $t=0$ the octopus is at rest, and its internal cavity contains a mass $m_{w}$ of water (so that the mass of the octopus plus water is $m_{o}+m_{w}$ ). It then starts to move by ejecting the water backwards at a constant rate $Q$ units of mass per unit time and at a constant speed $V$ relative to itself. The speed of the octopus at time $t$ is $u(t)$, and the mass of the octopus plus remaining water is $m(t)$. The drag force exerted by the surrounding water on the octopus is $\alpha u^{2}$, where $\alpha$ is a positive constant.

  Show that, during ejection of water, the equation of motion is

  $$m \frac{d u}{d t}=Q V-\alpha u^{2} .$$

  Once all the water has been ejected, at time $t=t_{c}$, the octopus has attained a velocity $u_{c}$. Use dimensional analysis to show that

  $$u_{c}=V f(\lambda, \mu)$$

  where $\lambda$ and $\mu$ are two dimensionless quantities and $f$ is an unknown function. Solve equation (1) to find an explicit expression for $u_{c}$, and verify that your answer is of the form given in equation (2).

  comment

Numbers and Sets

• 4.I.1D

  Numbers and Sets | Part IA, 2008

  Let $A, B$ and $C$ be non-empty sets and let $f: A \rightarrow B$ and $g: B \rightarrow C$ be two functions. For each of the following statements, give either a brief justification or a counterexample.

  (i) If $f$ is an injection and $g$ is a surjection, then $g \circ f$ is a surjection.

  (ii) If $f$ is an injection and $g$ is an injection, then there exists a function $h: C \rightarrow A$ such that $h \circ g \circ f$ is equal to the identity function on $A$.

  (iii) If $X$ and $Y$ are subsets of $A$ then $f(X \cap Y)=f(X) \cap f(Y)$.

  (iv) If $Z$ and $W$ are subsets of $B$ then $f^{-1}(Z \cap W)=f^{-1}(Z) \cap f^{-1}(W)$.

  comment

• 4.I.2D

  Numbers and Sets | Part IA, 2008

  (a) Let $\sim$ be an equivalence relation on a set $X$. What is an equivalence class of $\sim ?$ Prove that the equivalence classes of $\sim$ form a partition of $X$.

  (b) Let $\mathbb{Z}^{+}$be the set of all positive integers. Let a relation $\sim$ be defined on $\mathbb{Z}^{+}$by setting $m \sim n$ if and only if $m / n=2^{k}$ for some (not necessarily positive) integer $k$. Prove that $\sim$ is an equivalence relation, and give an example of a set $A \subset \mathbb{Z}^{+}$that contains precisely one element of each equivalence class.

  comment

• 4.II.5D

  Numbers and Sets | Part IA, 2008

  (a) Define the notion of a countable set, and prove that the set $\mathbb{N} \times \mathbb{N}$ is countable. Deduce that if $X$ and $Y$ are countable sets then $X \times Y$ is countable, and also that a countable union of countable sets is countable.

  (b) If $A$ is any set of real numbers, define $\phi(A)$ to be the set of all real roots of non-zero polynomials that have coefficients in $A$. Now suppose that $A_{0}$ is a countable set of real numbers and define a sequence $A_{1}, A_{2}, A_{3}, \ldots$ by letting each $A_{n}$ be equal to $\phi\left(A_{n-1}\right)$. Prove that the union $\bigcup_{n=1}^{\infty} A_{n}$ is countable.

  (c) Deduce that there is a countable set $X$ that contains the real numbers 1 and $\pi$ and has the further property that if $P$ is any non-zero polynomial with coefficients in $X$, then all real roots of $P$ belong to $X$.

  comment

• 4.II.6D

  Numbers and Sets | Part IA, 2008

  (a) Let $a$ and $m$ be integers with $1 \leqslant a<m$ and let $d=(a, m)$ be their highest common factor. For any integer $b$, prove that $b$ is a multiple of $d$ if and only if there exists an integer $r$ satisfying the equation $a r \equiv b \operatorname{(\operatorname {mod}m)\text {,andshowthatinthiscasethereare}}$ exactly $d$ solutions to the equation that are distinct $\bmod m$.

  Deduce that the equation $a r \equiv b(\bmod m)$ has a solution if and only if $b(m / d) \equiv 0$ $(\bmod m)$.

  (b) Let $p$ be a prime and let $\mathbb{Z}_{p}^{*}$ be the multiplicative group of non-zero integers $\bmod p$. An element $x$ of $\mathbb{Z}_{p}^{*}$ is called a $k$ th power $(\bmod p)$ if $x \equiv y^{k}(\bmod p)$ for some integer $y$. It can be shown that $\mathbb{Z}_{p}^{*}$ has a generator: that is, an element $u$ such that every element of $\mathbb{Z}_{p}^{*}$ is a power of $u$. Assuming this result, deduce that an element $x$ of $\mathbb{Z}_{p}^{*}$ is a $k$ th power $(\bmod p)$ if and only if $x^{(p-1) / d} \equiv 1(\bmod p)$, where $d$ is now the highest common factor of $k$ and $p-1$.

  (c) How many 437th powers are there mod 1013? [You may assume that 1013 is a prime number.]

  comment

• 4.II.7D

  Numbers and Sets | Part IA, 2008

  (a) Let $\mathbb{F}$ be a field such that the equation $x^{2}=-1$ has no solution in $\mathbb{F}$. Prove that if $x$ and $y$ are elements of $\mathbb{F}$ such that $x^{2}+y^{2}=0$, then both $x$ and $y$ must equal 0 .

  Prove that $\mathbb{F}^{2}$ can be made into a field, with operations

  $$(x, y)+(z, w)=(x+z, y+w)$$

  and

  $$(x, y) \cdot(z, w)=(x z-y w, x w+y z) .$$

  (b) Let $p$ be a prime of the form $4 m+3$. Prove that $-1$ is not a square $(\bmod p)$, and deduce that there exists a field with exactly $p^{2}$ elements.

  comment

• 4.II.8D

  Numbers and Sets | Part IA, 2008

  Let $q$ be a positive integer. For every positive integer $k$, define a number $c_{k}$ by the formula

  $$c_{k}=(q+k-1) \frac{q !}{(q+k) !}$$

  Prove by induction that

  $$\sum_{k=1}^{n} c_{k}=1-\frac{q !}{(q+n) !}$$

  for every $n \geqslant 1$, and hence evaluate the infinite $\operatorname{sum} \sum_{k=1}^{\infty} c_{k}$.

  Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of integers satisfying the inequality $0 \leqslant a_{n}<n$ for every $n$. Prove that the series $\sum_{n=1}^{\infty} a_{n} / n$ ! is convergent. Prove also that its limit is irrational if and only if $a_{n} \leqslant n-2$ for infinitely many $n$ and $a_{m}>0$ for infinitely many $m$.

  comment